Infrared Light Absorbance: a New Method for Temperature Compensation in Nondispersive Infrared CO2 Gas Sensor
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Nondispersive infrared CO2 gas sensor was developed after the simulation of optical cavity structure and assembling the optical components: IR source, concave reflectors, Fresnel lens, a hollow disk, and IR detectors. By placing a hollow disk in front of reference IR detector, the output voltages are almost constant value, near to 70.2 mV. The absorbance of IR light, Fa, shows the second order of polynomial according to ambient temperatures at 1,500 ppm. The differential output voltages and the absorbance of IR light give a higher accuracy in estimations of CO2 concentrations with less than ± 1.5 % errors. After implementing the parameters that are dependent upon the ambient temperatures in microcontroller unit (MCU), the measured CO2 concentrations show high accuracies (less than ± 1.0 %) from 281 K to 308 K and the time constant of developed sensor is about 58 sec at 301 K. Even though the estimation errors are relatively high at low concentration, the developed sensor is competitive to the commercial product with a high accuracy and the stability.
Keywords:
Nondispersive infrared gas sensor, Optical simulation, Optical cavity structure, Absorbance of IR, Temperature compensation1. INTRODUCTION
NDIR (Nondispersive infrared) gas sensor uses optical properties of target gases and, generally, it consists of three optical components: infrared (IR) light source, optical cavity structure, and infrared detectors. Because it uses solid-state components and its operating principle is based upon the absorption of IR by the target gas, so the aging and contamination problems caused in electrochemical sensor can be alleviated. In addition, the selectivity of sensor for the absorbing gas can be acquired by adopting an optical band-pass filter in front of IR detectors: thermopile or pyroelectric detectors [1, 2]. Even though NDIR gas sensor has a good selectivity and stability compared to the electrochemical type, the IR source could be aged after long operating times because of the deterioration of tungsten filament in IR source. So, the more robust and continuous IR source is fabricated by MEMS (Mircroelectromechanical systems) techniques and it is available in the market place [3, 4]. However, NDIR gas sensor potentially needs temperature compensation and offset calibration at the final quality control procedures because the properties of IR source and detector depend upon the ambient temperature [5, 6]. Furthermore, the sensitivity of NDIR sensor depends mainly on the optical cavity structure and the IR detector itself because the Beer-Lambert law governs it [7-9]. However, if the users properly select the IR detector, the sensitivity of NDIR gas sensor is solely dependent upon the optical cavity structure itself, so this issue will be discussed later in the background of NDIR gas sensor.
TOC (total organic carbon) measurement systems need CO2 gas to estimate the organic carbon concentration in water because byproducts of livestock and other contamination sources contaminate the rivers and streams. So many developed countries are using TOC systems to manage the quality of water now, and TOC systems currently use two sensor types for assuring the quality of water: NDIR and permeable membrane types [10-12]. In terms of autonomous systems and ubiquitous society, compact size and convenient sensor systems are more user-friendly than the bulky one. This might be one of the reasons to choose NDIR CO2 gas sensor for TOC system so far. However, TOC system generates the toxic gases (mainly acids) and water vapors during the ultraviolet or thermal combustion processes in TOC systems. Therefore, the above-mentioned molecules should not affect NDIR gas sensors and they should have high sensitivity in order to reduce the quantity of sampled water and have a long-term stability, adequate temperature compensation methods and enhance the efficiency of TOC systems [13].
This article discusses about the previously researched optical cavity structures to figure out the requested performance in NDIR gas sensors and a revised model to develop a new sensor that improve the above mentioned technical issues. Also, the author describes a new method how to accurately compensate the temperature effect with the absorbance of infrared light and calculate the temperature-compensated concentrations. Finally, after temperature compensation the stability of sensor module has been performed to validate the compatibility of developed sensor with the commercial one.
2. TECHNICAL ISSUES AND PROTOTYPING OF SENSOR MODULE
2.1 Background of optical cavity structure
The basic components of NDIR gas sensor are IR source, optical cavity (or gas cell/chamber denoted in previous articles), and IR detector with a narrow band-pass filter at the end of optical cavity structure. The Lambert-Beer law as described in Eq. (1) explains the attenuation of IR energy after transmitting the optical cavity that contains IR absorbing gas molecules and the transmitted energy generates the voltage at the IR detector Vd(T,x) as shown in Eq. (2) [13, 14].
| (1) |
| (2) |
These equations explain the relationship between transmitted IR energy and output voltage after traveling the optical cavity structure characterized by the product (β(T)) of absorption coefficient (σ) of target gas and optical path length (l), initial IR intensity (Io) and target gas concentrations (x). Because the optical filter has a passband of IR light (which is around 180 nm), there are non-absorbing wavelengths of IR by the target gas. It causes the generation of output voltages (Vo(T)). Also, the IR source and filter properties can be also affected by the ambient temperature, furthermore, the activation of gas molecules also shows temperature dependency, these cause the output voltages (α(T)) that consider temperature dependent absorption property of gas molecules and filter in Eq. (2).
To obtain a good sensitivity and signal-to-noise ratio (S/N), the sensor needs a large optical path length and the intensity of IR light enhances the performance in order to overcome the surrounding optical noise as suggested in previous article [15]. The modulation mentioned above two factors (path length and intensity at the detector) can improve the basic performance of sensor, so the researchers focused onto these issues in order to discriminate or improve the performance of NDIR gas sensors as described below.
Johann et al. [16] modeled two different optical cavity structures and simulated their properties by using commercial ray tracing package. As they suggested in their article, the product (β(T)) of optical path length (l) and gas absorption coefficient (σ) and the incident angle (γ) into the IR detector are the major parameters in terms of the output voltage changes according to the variation of gas concentrations. Furthermore, their simulation results revealed that the rotational symmetric ellipsoid (principal axis is 55 mm) presented higher sensitivity compared to the cylindrical multi-reflection structure (length is 25 mm). The detector received the most of the rays and the sensor increased the sensitivity to certain range of gas concentration by the multiple reflection structure (the optical path length was 980.5 mm in average). By using ellipsoidal optical structure, it focused the IR light at the detector placed at the focal point and then it improved the output voltages and the S/N ratio. The experimental and the simulation results reported by the authors proved the above-mentioned issues before [15, 17, 18].
Other multi-pass cells were suggested by two groups: Hök et al. [19] and J.S. Park [20] and H.G. Park et al. [15, 21]. Hök et al. used three elliptical reflectors within 40 mm × 40 mm × 14 mm and the path length of gas cell was roughly 210 mm. J.S. Park simulated the gas cell used in methane detection sensor and proposed a new structure consisted of two elliptical reflectors. In their simulation results, the rays were distributed whole areas of detector surfaces in both cases without focusing of incident rays. Their sensors showed about ±30 ppm accuracies at room temperature. Another solution for high sensitivity NDIR gas sensor reported by Hök et al. adopted White-Cell structure [22] to increase the optical path length around 1 m distance with roughly 70 mm × 90 mm × 20 mm footprint [23]. This sensor showed a very high resolution around one ppm range in their report. The author tried to enhance the performance of NDIR gas sensor by adopting above mentioned properties: long optical path length and focusing of IR light at the detector to improve the SNR of NDIR gas sensor.
2.2 Design and simulation of optical cavity structure
The increment of optical path length and focusing the irradiated IR energy at the detector enhance the performance of NDIR gas sensor. To achieve the first purpose, the optical structure with a long path-length has been surveyed: White-cell [19, 21, 22, 24] and Herriott cell [25] structures. By using Herriot cell, a very large optical path can be achieved; however, the dimension of optical structure is limited in this research, so the White-cell structure was chosen.
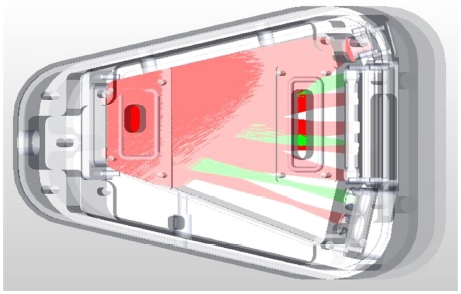
The White-cell consists of three concaved reflectors: two small reflectors for changing the direction of incoming light, a relatively large reflector for transmitting the light to the small reflectors. Three reflectors were made of fused-silica substrates coated with Au/Cr (100 nm/150 nm) thin films with the same radius of curvature (80 mm). After Au deposition onto the reflectors, 50 nm thick SiO2 film has been deposited for anti-scratching. However, silicon oxide film has a hydrophilic property, so a 0.5 μm thick hydrophobic film (Parylene-C film) deposited onto Au/Cr/fused-silica substrates to prohibit the condensation of water vapor at the mirror surfaces of reflectors.
Fig. 1 shows the modeled optical cavity structure and a ray tracing result of designed optical cavity structure with a commercial ray tracing software named TracePro®. Even though the IR source has a parabolic reflector, the IR light radiated from the source has roughly ±10o incident angles, so the some of the IR light reach to the walls of optical cavity structure as shown in Fig. 1. The IR light emitted from IR source arrives at the IR detector (CO2 detector side) after traveling 980 mm distance. However, some of the IR light reflects only once at the lower part of two small reflectors at the left side of Fig. 1, so the path length is about 160 mm from IR source to the reference detector.
2.3 Prototyping of optical cavity structure
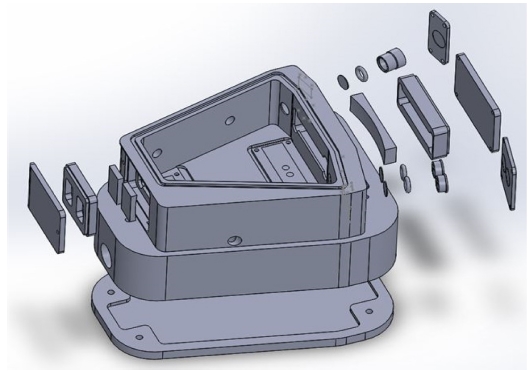
In order to enhance the performance of NDIR gas sensor, available parts for optical cavity structure are considered and modeled. Fig. 2 gives the modeled whole components of optical cavity structure.
In front of IR source (located in right upper corner), there are two components (O-ring and sapphire window, Edmond optics, USA) for the protection of gas leakage and for prohibiting the fluctuation of surface temperature of IR source according to the flow of injected gas. The main reflector located at the center of right side is inserted in the metal cassette and the metal plate cramps the cassette for fixing two parts: main reflector and cassette. Two IR detectors are soldered onto small PCB (printed circuit board) shown at the lower right corner in Fig. 2, then it is assembled on the body of optical cavity structure. The Fresnel Lens (Edmond Optics, USA) and O-ring were placed in front of CO2 detector for focusing the IR light and for prohibiting gas leakage, however, a hollow disk (diameter 1.0 mm) for modulating the output voltage of reference IR detector and O-ring were positioned to decrease the incoming IR energy and for anti-gas leakage at the reference detector. Two relatively small reflectors also were inserted into the metal cassette and they were aligned with a metal plate as can be seen. The O-ring was used for sealing the optical cavity structure from the outside environment. Underneath the optical cavity structure, the signal conditioning circuit board is placed and it isolates from the outside circumstance by the cover plate as shown at the bottom side of Fig 2.
2.4 Circuit Design
The functional block of signal conditioning circuit and the fabricated PCB is shown in Fig. 3. The electrical powers were divided into two parts (analog & digital power supply units) to acquire the stability of digital power supply because the IR source consumes a high power (around 600 mW) during the electrical chopping status. The analog voltage (9 V) is supplied to lamp driving IC (TPS7A49, Texas Instruments, USA) and the variable resistor is used to adjust the peak analog voltage applied to thermal IR source (INTX MIRL17-900, Importec, Italy). The pulse-on and off time are modulated by the algorithm implemented in MCU (dsPIC30F4013, Microchip, USA). The thermopile IR detectors (HIS A21 E4.26 G5600 & HIS A21 E3.91 G5600 Heimann sensors GmbH, Germany) used in this research consists of thermopile chip and pre-amplification IC in the TO-5 packages. The pre-amplified detector signals were amplified again by low offset and drift integrated circuit chip (MAX4239, Maxim Integrated Products Inc.) and they are converted to digital signals for further signals conditioning. Also the output signals from the second stage operational amplifier were differentially amplified to achieve high difference output voltage. Then three analog signals and output voltage developed by the bridge circuit with temperature sensor (Pt-100 Ω, USA sensors, USA) were converted to digital signals by analog-to-digital converter (ADC, ADS1115, Texas Instruments, USA) to transmit and also calculate CO2 concentrations and ambient temperature. The digital signal was converted to the analog by digital-to-analog converter (which is not shown in block diagram: DAS8574, Texas Instruments, USA) and the converted analog voltage feeds to the output port. The other modulated signals transmitted to the RS-485 chip (ADM4850, Analog Devices, USA) for the final data acquisition and storage further analysis of data.
3. EXPERIMENTAL SETUP
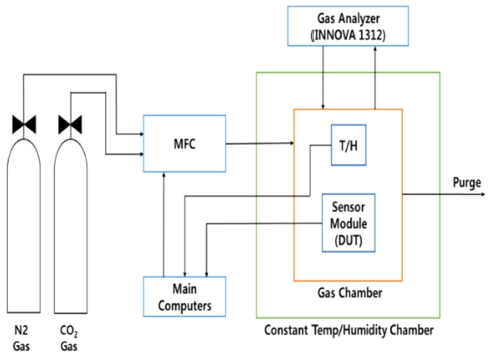
After prototyping the sensor modules as previously reported [18], they were tested several months to get reliable experimental results. The block diagram of measurement system is described in Fig. 4. Inside of constant temperature-humidity chamber, a small gas chamber was installed to contain the sensor modules and to measure the output properties of them according to the temperature and gas concentration variations. The whole measurement system consists of four parts as shown in Fig. 4: gases and gas injection module, constant temperature-humidity chamber, data storage computers, and gas monitoring system.
The carbon dioxide gases are used as seven standard measurements: 100, 200, 500, 1000, 1500, 3000, 5000 ppm. Each gas was connected to the main MFCs (Mass Flow Controllers) and the valves were switched to inject the specific concentration of CO2 gas. However, the standard gas concentrations were monitored separately by using the plastic bag (Non odor bag, BMS 0422-42-5748, Japan) in order to provide accurate standard concentration of gases for regression analysis. The gas flow rate was 500 standard cubic centimeters per minute (SCCM) during the whole measurements. After setting the ambient temperature, the gas chamber was purged with a high purity nitrogen gas (99.9999%) to get nearly 0 ppm CO2 concentrations. The output voltages of sensor modules according to CO2 concentrations and ambient temperatures were saved in the main computers through RS-485 ports.
The measurement apparatus is depicted in Fig. 4 and the arrows shows that the directions of gases and data from the sensor and analyzer. During the measurements of sensor modules, one commercial sensor (Vaisala, GMP343, Finland) was serially connected to the fabricated sensor module for the comparison. The experiments were executed ten times at the same testing conditions.
The data were analyzed by a commercial software named Sigma plot for further data processing and also drawing the experimental results. Finally, the temperature dependent parameters and coefficients were analyzed and they were used to estimate and supply the temperature-compensated concentrations of CO2 gas.
4. RESULTS AND DISCUSSIONS
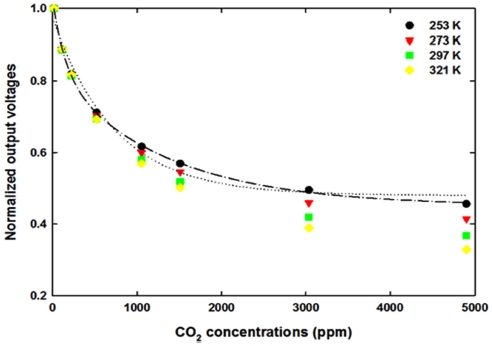
The output voltages of IR sensors are known to be governed by Eq. (2) as described, however, some of the experimental results showed that the regression of results did not follow it and showed more complex equation presented by five-parameter to represent the results of experiment [26]. The similar situation occurred in this research as shown in Fig. 5. The output voltages shown in Fig. 5 are average values of output voltages at each experimental condition as a function of CO2 concentrations and ambient temperatures from 254 K to 321 K. The output voltage at 0 ppm CO2 concentrations increases as the ambient temperatures increase because the ambient temperature increases that of IR source, so the intensity of IR radiation enhances as reported in the articles [17, 18, 21]. However, the decrement of output voltages seems to follow different trends according to the CO2 gas concentrations and ambient temperatures. When the data at 253 K are assumed to follow three parameters (Vo, α, β) as suggested in Eq. (2), the coefficient of correction, R2, shows 0.9843 (dotted line in Fig. 5). As can be seen in Fig. 5, the dotted line (which is regressed by three parameters as similar to Eq. (2)) deviates from the experimental data points. When the data were analyzed by five-parameter, the regression line (dash-dotted line, R2 = 0.9995) matches well with the experimental data points. This might be interpreted that the sensor module has at least two different optical path lengths as suggested by S.H. Yi et al. [26], T.A. Vincent and J.W. Gardner [27], and the related equation will be as below Eq. (3).
| (3) |
where α1(T) and α2(T) are the offset values and β1(T) and β2(T) are the products of optical path and gas absorption coefficient depending on the optical path lengths at temperature. T.
Even though the data points are followed by particular equation with high accuracies, if the equation of regression cannot be implemented in the algorithm of MCU (micro-controller unit), the regressed equation will not be useful in prototyping of sensor. So the author tried to figure out how to estimate the exact gas concentrations with three parameters.
L. Jun et al. [13, 28] suggested the absorbance Fa, to estimate the concentration of target gas is as described in Eq. (4)
| (4) |
where, Vo is the output voltage of gas sensor at certain temperature and gas concentration, Vγ is the output voltage of reference sensor at the same condition, and Z is the voltage ratio of Vo and Vγ at zero ppm and a specific temperature.
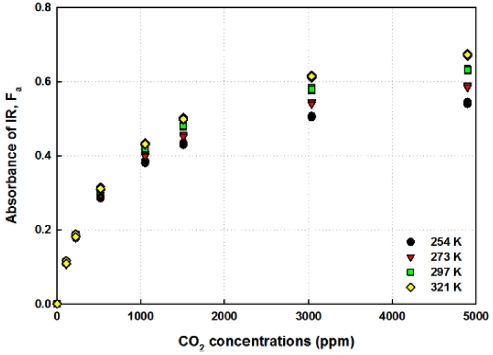
However, the absorbance defined in Eq. (4) should be properly selected to estimate the correct concentrations of target gas because it is dependent on the ambient temperature and gas concentrations [13] as shown in Fig. 6. As the gas concentration gets higher, the absorbance increases and it shows a temperature dependency at each gas concentration shown in Fig. 6.
The reductions of output voltages and the absorbance of IR light are temperature dependent, as shown in Fig. 5 and Fig. 6. The decrement of output voltage at low temperature (254 K) is large below 1,000-ppm CO2 concentrations and the maximum difference of absorbance is around 0.475. However, the output voltage difference between 0 ppm and 5,000 ppm is about 584 mV and the maximum difference of absorbance is around 0.616 at 321 K ambient temperatures. The changes between the outputs mean that the parameter, β(T), suggested in Eq. (2) depends upon the ambient temperature and it reveals that the absorption coefficient of gas shows a temperature dependency. Even though it is different from the previous researches [27, 28], the results obtained in this research are more reasonable because the gas molecules will be more activated as the ambient temperatures are increased and the optical path length will not be enlarged with 80 K temperature increase. Furthermore, the absorption coefficient is dependent on the ambient temperature as suggested by W.B. DeMore [29]. So, the temperature dependent absorption of target gas should be determined to estimate the exact concentrations after the measurements.
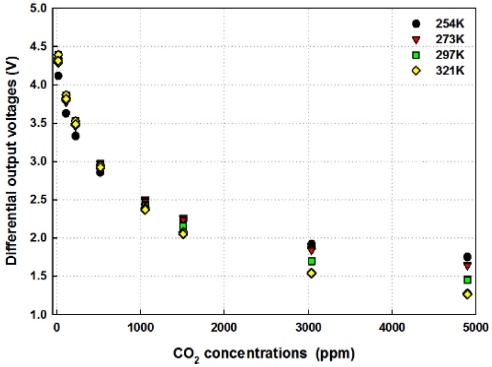
The voltage difference between 0 ppm to 5,000 ppm ranges from 450 mV to 650 mV as can be seen in Fig. 5 and it is dependent on the ambient temperature. So the output voltages of CO2 detector were subtracted with those of reference IR detector and they were amplified again. The difference of differential output voltages showed about 3 V from 0 ppm to 5,000 ppm ranges at 321 K ambient temperature as shown in Fig. 7.
The decrement trends of output voltages below 273 K are quite different from the other experimental results and the output voltages were almost saturated above 3,000 ppm. The voltage decrement from 0 ppm to 5,000 ppm is about 2.366 V. However, above 273 K temperatures, the decrement of output voltage doesn’t show the saturation trend and also the total voltage decrements show the average value of 2.909 V at 297 K and 3.070 V at 321 K.
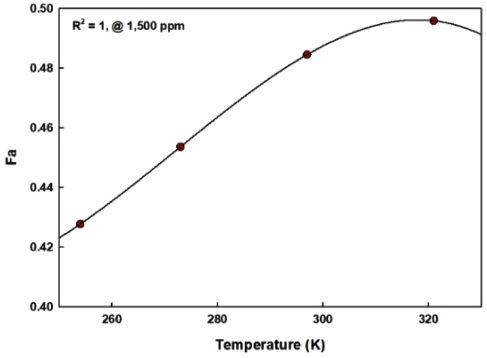
As described in Fig. 6, the absorbance of IR light is dependent upon the ambient temperatures and also CO2 gas concentrations. And the output voltages shown in Fig. 5 and Fig. 7 can be regressed by the summation of two exponential functions with a high correction coefficient above R2 > 0.99. However, as far as the author knows, it is very difficult to get a function to predict the estimation concentration of CO2 gas with two exponential functions. Furthermore, as can be seen in Fig. 5 and Fig. 7, the decrement pattern of the outputs is quite different between low concentration and high CO2 concentrations. So, the proper selection of absorbance, Fa, is very important to predict the concentrations of CO2 gas with the equation described in Eq. (2). When the absorbance is selected at low concentration, for example at 500 ppm, the estimation error of CO2 concentrations was above 10 % from 3,000 ppm. So, absorbance at 1,500 ppm CO2 concentrations was selected and presented as a function of ambient temperatures in Fig. 8. As presented in Fig. 8, the correction coefficient, R2, is equal to 1 and so the second order of polynomial analyzed by regression can be used as a criterion to choose the subprogram in MCU and to calculate the measured CO2 concentrations.
Before implementing the codes for estimating the concentrations of CO2 gas, the measured data were used to calculate the concentrations of CO2 gas with the temperature dependent functions as presented in previously reported article [17] and the equations shown in Eq. (2) and Eq. (4). From the Eq. (2), the estimated CO2 concentrations are as follows
| (5) |
where Vd(T, x), Vo(T), α(T), and β(T) can be acquired from the regression analysis.
The main difference between the previous research [27, 28] and the current one is the temperature dependency of the product (β(T)) of gas absorption coefficient and optical path length. As suggested in previous report [17], the gas absorption parameter, β(T), is dependent upon the ambient temperatures and can’t be considered as a constant value described in articles [27, 28]. If it is considered as a constant value, the temperature compensation errors were relatively high compared to the estimations derived with temperature dependent gas absorption parameter, β (T).
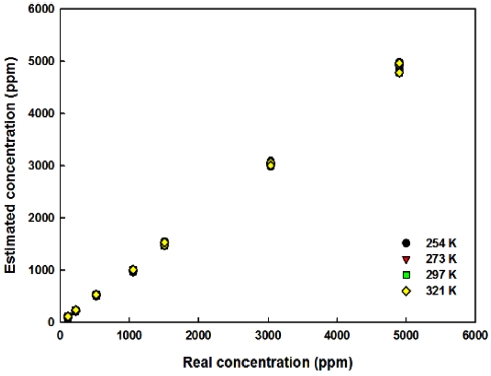
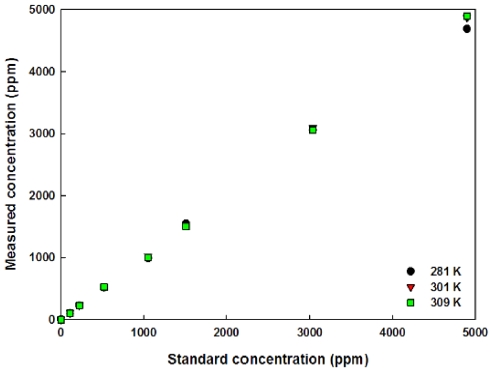
Based on the above consideration and the equations, the estimated CO2 concentrations are shown in Fig. 9. In Fig. 9, the estimations of CO2 concentrations are derived by using the differential output voltages shown in Fig. 7. From 200 ppm to 3,000 ppm CO2 concentrations, the estimation errors were in the range from -7.3 % to 4.3 % throughout the ambient temperatures and also CO2 concentrations and the average errors were in the range of ± 2.5 %. However, the errors were relatively high (> 10 %, which is similar to the results measured from the commercial product) at low and high CO2 concentrations (around -4 %). Excluding the data acquired below 274 K, the estimation errors in Fig. 9 were around 1.2 %.
Because the estimation errors were relatively small in case of using differential output voltages, the codes for the calculations of measured CO2 concentrations were programed by using those values. Then measured values according to the random temperature variations are shown in Fig. 10. As presented in Fig. 10, the measurement errors were less than ± 1.0 % except low (the highest error was about -11 % at 110 ppm) CO2 concentrations, so the developed sensor shows a very high accuracy and also appropriately temperature compensated structure with a reference detector that has a hollow disk to diminish the intensity of incoming infrared energy, long optical path length (around 980 mm), and also Fresnel lens for focusing IR light.
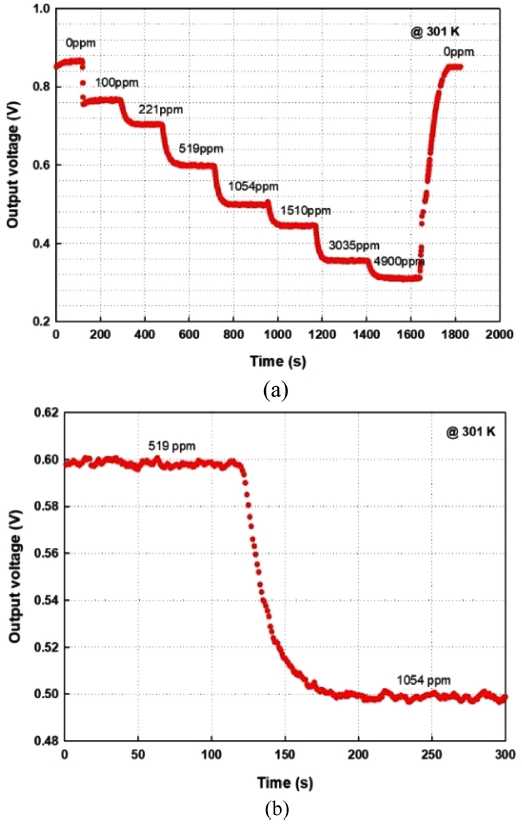
Fig. 11 presents the recovery of developed sensor module and time constant at 301 K ambient temperature. The developed sensor shows an excellent recovery from 0 ppm to 4950 ppm and when it purges with the high purity nitrogen gas to reach the initial condition as shown in Fig. 11 a). The time constant, τ, of developed CO2 sensor gives about 58 seconds in this research. It is recognized as a competitive sensor module compared to the commercial product tested in these experiments.
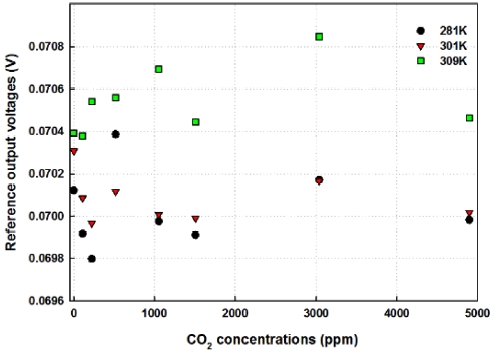
As presented from Fig. 7 to Fig. 10, the differential output voltages give the reliable and accurate results. The absorbance of IR light is dependent upon the variation of temperature at the same CO2 concentrations as shown in Fig. 6 and Fig. 8. This suggests that the absorption coefficient shows a strong temperature dependent characteristics because the output voltages of reference sensor are almost constant as shown in Fig. 12 and it contributes to the decay of exponential function described in Eq. (2). Also it gives a good criterion for selecting and calculating the measured concentrations of CO2 gas. With the application of the absorbance of IR light, the accuracy of measured CO2 concentrations could be enhanced with the small errors ranged from -1 % to +1 %. It gives very competitive experimental results compared to the commercial product tested in this experiment.
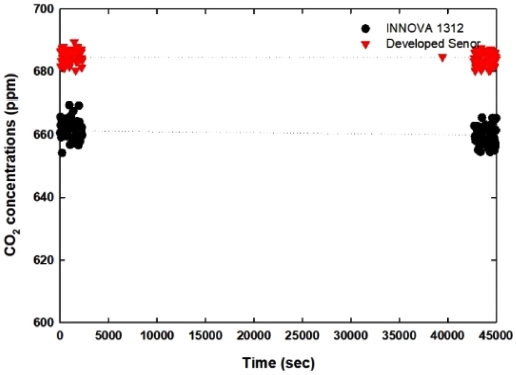
Fig. 13 shows the stability result of the developed sensor module compared to the commercial product for 12.5 hours. At the beginning of the test, even the developed sensor showed the average 22 ppm higher measurement results, it showed a similar standard deviation 14.12 ppm compared to that of commercial product, 14.78 ppm. After 45000 seconds later, there were slight decrements of measured values, that might be the micro-leakage of gas chamber, however the deviation of measurement quite similar to the previous values.
Because the developed sensor module shows a high accuracy and the stability, it could be an another alternative sensor for TOC system and other applications.
5. CONCLUSIONS
With the 3-D modeling of every components of sensor module and the simulation results of optical cavity structures, NDIR CO2 gas sensor for TOC system has been successfully fabricated and tested in this research. By installing a hollow disk in front of a reference detector, the temperature dependency of reference sensor could be alleviated. Therefore, the differential output voltages of IR sensors are affected by only the output voltages of CO2 gas sensor. Because there are more than two different optical path in the cavity structure, IR absorbance has been proposed as a new criterion for the estimation of gas concentrations. With the adoption of absorbance of IR light, the output voltages of CO2 sensor could be accurately regressed and the measurements of CO2 concentrations was enhanced with ± 1 % accuracy. The accuracy, time constant and the stability of a developed sensor for TOC system are very competitive to the commercial product.
Acknowledgments
This research was supported by the R&D Center for Green Patrol Technologies through the R&D for Global Top Environmental Technologies funded by the Ministry of Environment, Republic of Korea (MOE).
References
- http://heimannsensor.com, (retrieved on Jan. 2, 2019).
- http://www.infratec.ed, (retrieved on Jan. 2, 2019).
- http://www.hawkeyetechnologies.com, (retrieved on Jan. 2, 2019).
- http://www.eot.it, (retrieved on Jan. 2, 2019).
- R. Eisberg and R. Resnick, Quantum physics of atoms, molecules, solids, nuclei, and particles, John Wiley and Sons, New York, pp. 1-25, 1985.
-
J. H. Kim and S. H. Yi, “Effects of temperature and humidity on NDIR CO2 gas sensor”, J. Sens. Sci. Technol., Vol. 26, No. 3, pp. 179-185, 2017.
[https://doi.org/10.5369/JSST.2017.26.3.179]

-
J. Hodgkinson, R. Smith, W. O. Ho, J. R. Saffell, and R. P. Tatam, “Non-dispersive infra-red (NDIR) measurement of carbon dioxide at 4.2 μm in a compact and optically efficient sensor”, Sens. Actuators B, Vol. 186, pp. 580-588, 2013.
[https://doi.org/10.1016/j.snb.2013.06.006]

-
A. Sklorz, S. Janßen, and W. Lang, “Detection limit improvement for NDIR ethylene gas detectors using passive approaches”, Sens. Actuators, Vol. 175, pp. 246-254, 2012.
[https://doi.org/10.1016/j.snb.2012.09.085]

-
J. H. Han, S. W. Han, S. M. Kim, J. J. Park, and S. Moon, “High detection performance of NDIR CO2 sensor using stair-tapered reflector”, IEEE Sens. J., Vol. 13, No. 8, pp. 3090-3097, 2013.
[https://doi.org/10.1109/JSEN.2013.2262268]

- http://www.ssi.shimadzu.com, (retrieved on Jan. 3, 2019).
- http://www.vaisala.com, (retrieved on Jan. 3, 2019).
- http://www.geinstruments.com, (retrieved on Jan. 3, 2019).
- J. H. Kim, H. G. Park, and S. H. Yi, “IR absorbance as a criterion for temperature compensation in nondispersive infrared gas sensor”, Proc. Eurosens., p. P9-ID 7106, Graz, Austria, 2018.
- J. H. Kim, S. H. Shin, and S. H. Yi, “Effects of infrared energy on dual elliptical NDIR ethanol gas sensors”, Proc. Eurosens., p. T-CS-302-1083, Paris, France, 2017.
-
J. S. Park and S. H. Yi, “Nondispersive infrared ray CH4 gas sensor using focused infrared beam structures”, Sens. Mater., Vol. 23, No. 3, pp. 147-158, 2011.
[https://doi.org/10.18494/SAM.2011.681]

-
J. Mayrwöger, P. Hauer, W. Reichl, R. Schwödiaer, C. Krutzler, and B. Jakoby, “Modeling of infrared gas sensors using a ray tracing approach”, IEEE Sens. J., Vol. 10, No. 11, pp. 1691-1698, 2010.
[https://doi.org/10.1109/JSEN.2010.2046033]

-
J. H. Kim, K. H. Lee, and S. H. Yi, “NDIR ethanol gas sensor with two elliptical optical structure”, Procedia Eng., Vol. 168, pp. 359-362, 2016.
[https://doi.org/10.1016/j.proeng.2016.11.122]

- J. H. Kim, J. Y. Lee, K. H. Lee, and S. H. Yi, “Enhanced characteristics of nondispersive infrared CO2 gas sensor by deposition of hydrophobic thin film”, Proc. Eurosens., p. M-CS-302-1084, Paris, France, 2017.
-
B. Hök, H. Petterson, A. K. Anderson, S. Haasl, and P. Åkerlund, “Breath analyzer for alcolocks and screening devices”, IEEE Sens. J., Vol. 10, No. 1, pp. 10-15, 2010.
[https://doi.org/10.1109/JSEN.2009.2035204]

-
J. S. Park, H. C. Cho, and S. H. Yi, “Temperature compensated NDIR CH4 sensor with focused beam”, Procedia Eng., Vol. 5, pp. 303-306, 2010.
[https://doi.org/10.1016/j.proeng.2010.09.108]

- H. G. Park and S. H. Yi, “Analysis of Output voltage properties of non-dispersive infrared gas sensors according to ambient temperatures”, J. Sens. Sci. Technol., Vol. 27, No. 5, pp. 294-299, 2018.
-
J. U. White, “Long optical paths of large aperture”, J. Opt. Soc. Am., Vol. 32, No. 5, pp. 285-288, 1942.
[https://doi.org/10.1364/JOSA.32.000285]

-
C. Hummelgård, I. Bryntse, M. Bryzgalov, J. Å. Henning, H. Matin, M. Norén, and H. Rödjegård, “Low-cost NDIR based sensor platform for sub-ppm gas detection”, Urban Clim., Vol. 14, pp. 342-350, 2015.
[https://doi.org/10.1016/j.uclim.2014.09.001]

- A. K. Zaouk, M. Wills, E. Traube, and R. Strassburger, “Driver alcohol detection system for safety (DADSS) – A Status update”, Proc. ESV 2015, p. 15-0276, Gothenburg, Sweden, 2015.
-
M. Guinet, A. W. Mantz, and D. Mondelain, “Performance of a 12.49 meter folded path copper Herriott cell designed for temperatures between 296 and 20 K”, Appl. Phys. B, Vol. 100, No. 2, pp. 279-282, 2010.
[https://doi.org/10.1007/s00340-010-3946-5]

-
S. H. Yi, Y. H. Park, and J. K. Lee, “Temperature dependency of non-dispersive infrared carbon dioxide gas sensor by using White-Cell structure”, J. Sens. Sci. Technol., Vol. 25, No. 5, pp. 377-381, 2016.
[https://doi.org/10.5369/JSST.2016.25.5.377]

-
T. A. Vincent and J. W. Gardner, “A low cost MEMS based NDIR system for the monitoring of carbon dioxide in breath analysis at ppm levels”, Sens. Actuators B, Vol. 236, pp. 954-964, 2016.
[https://doi.org/10.1016/j.snb.2016.04.016]

-
L. Jun, T. Qiulin, Z. Wendong, X. Chenyang, G. Tao, and X. Jijun, “Miniature low-power IR monitor for methane detection”, Measurement, Vol. 44, pp. 823-831, 2011.
[https://doi.org/10.1016/j.measurement.2011.01.021]

-
W. B. DeMore and M. Patapoff, “Temperature and Pressure Dependence of CO2 Extinction Coefficients”, J. Geophys. Res., Vol. 77, No. 31, pp. 6291-6293, 1972.
[https://doi.org/10.1029/JA077i031p06291]