온도 보상을 이용한 자기변형 위치 센서의 정확도 향상 방법
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/bync/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
An ultrasonic based magnetostrictive position sensor (MPS) provides an indication of real target position. It determines the real target position by multiplying the propagation speed of ultrasonic wave and the time-of-flight between the receiving signals; one is the initial signal by an excitation current and the other is the reflection signal by the ultrasonic wave. The propagation speed of the ultrasonic wave depends on the temperature of the waveguide. Hence, the change of the propagation speed in various environments is a critical factor in terms of the positioning accuracy in the MPS. This means that the influence of the changes in the waveguide temperature needs to be compensated. In this paper, we presents a novel way to improve the positioning accuracy of MPSs using temperature compensation for waveguide. The proposed method used the inherent measurement blind area for the structure of the MPS, which can simultaneously measure the position of the moving target and the temperature of the waveguide without any additional devices. The average positional error was approximately -23.9 mm and -1.9 mm before and after compensation, respectively. It was confirmed that the positioning accuracy was improved by approximately 93%.
Keywords:
Magnetostrictive position sensor, Temperature compensation, Ultrasonic wave, Waveguide1. 서 론
시스템의 제어나 상태 감시를 목적으로 한 여러 물리 량의 측정 기술은 많은 산업 분야에 적용되고 있으며 기술 발전에 따라 측정 기술에 대한 정확도, 정밀도, 신뢰도 및 주변 환경에 대한 강건함 등의 요구 조건 역시 높아지고 있다. 측정된 여러 물리 량은 대부분 시스템의 제어나 상태 감시의 목적으로 활용되는데 위치 측정 기술은 주로 유압 시스템의 실린더 및 가공 스테이지의 위치 제어, 선박이나 석유화학 등 유체 저장소의 액위 측정에 적용된다[1]. 온도 측정 기술은 발전소, 선박, 항공, 자동차, 기계제조산업 등에 많이 사용되고 있다. 이러한 위치나 온도 측정 기술을 구현하는데 있어 보편 적으로 사용되는 방법 중 하나가 초음파 방식이다.
초음파 방식은 기체를 매질로 사용하는 것이 일반적이며 고체를 매질로 이용하기도 한다. 초음파 송신부에서 발생된 초음파가 매질을 따라 전파되다 측정하고자 하는 대상에 부딪혀 반사되어 돌아오는 반향파를 초음파 수신부에서 받는데 이때의 초음파 전파 시간을 위치나 온도로 변환한다.
기체를 매질로 하는 경우, 초음파 송·수신부와 측정하고자 하는 대상 사이에 장애물이 없어야 하며 표면이 깨끗하게 유지되어야 난반사나 산란을 줄일 수 있다. 고체를 매질로 하는 경우, 초음파의 전파는 해당 매질로 한정되기 때문에 먼지나 물 등과 같은 외부 환경에 강건한 특징이 있다. 이 때, 해당 고체를 초음파 도파로, 초음파 도파로를 따라 전파되는 초음파를 유도 초음파(Guided wave)라고 한다[2,3].
자기변형 위치 센서(Magnetostrictive Position Sensor, MPS)는 자기변형효과(Magnetostrictive effect)를 이용해 초음파 도파로 자체의 변형으로 초음파를 발생시킨다. 자기변형효과는 자기장 내에서 강자성체의 외형이 변하는 현상을 의미하여 주로 구동기에 많이 이용된다. 이와 반대로 재료에 외력을 가해 재료의 외형이 변하게 되면 재료 자체의 투자율이 변화하는 역자기변형효과는 주로 센서나 에너지 하베스팅 쪽에 많이 이용된다.
위치 측정 기술은 초음파의 발생 위치의 변화에 따라 초음파의 전파 시간이 바뀌기 때문에 해당 전파 시간을 통해 위치를 검출해 내는 방식이다. 온도 측정 기술은 초음파 전파 속도가 초음파 도파로의 온도에 의존적이기 때문에 동일한 위치에서 초음파가 발생한다 하더라도 온도에 따른 초음파 전파 속도가 달라지므로 그 변화로 온도를 측정하게 된다.
이에 본 연구에서는 자기변형원리를 이용한 초음파 방식의 위치 및 온도에 대한 동시 측정 할 수 있는 방법을 연구한다. 일반적인 위치 측정 시스템은 상온에서 동작하며 적용 온도 변동폭이 넓지 않지만 그렇지 않은 경우에는 온도에 따른 초음파 전파 속도의 변화로 인해 위치 측정 오차를 야기 할 수 있으므로 이를 보상하기 위한 별도의 시스템을 내장한다
본 연구에서 제안하고자 하는 위치 및 온도에 대한 동시 측정 방법은 별도의 추가 장치 없이 위치 측정 시스템의 구조에서 오는 고유 측정 불감대 영역을 이용하고, 반사되어 돌아오는 반향 파를 검출하는 수신 코일의 구조 변환을 통해 이루어진다.
이를 통해 단일 장치로 위치와 온도를 동시에 측정하고, 측정된 온도 값을 이용함으로써 주변 환경 변화에 따른 초음파 도파로의 온도 변화로 야기될 수 있는 측정 대상의 위치 오차 보정을 자체적으로 수행할 수 있도록 한다.
2. 자기변형 위치 센서
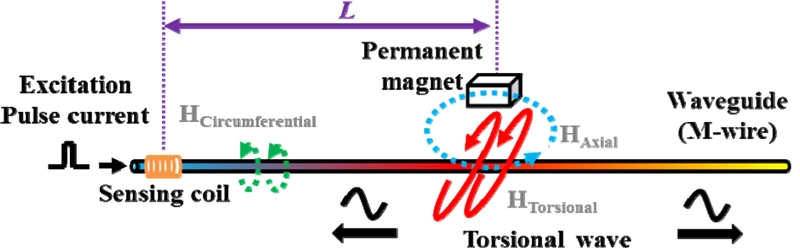
자기변형 위치 센서는 신호를 보내는 발신부와 되돌아오는 비틀림 파를 유도 전압 형태로 받는 수신부를 모두 가지고 있어 트랜스듀서라고도 한다[4]. 자기변형원리를 이용한 초음파 위치 측정 원리는 Fig. 1에 나타나 있다. 중앙에 와이어 형태의 자기변형재료(Magnetostrictive wire, M-wire)가 있고, 재료에 일정한 크기의 축 방향 자기장을 지속적으로 인가하기 위한 영구자석(Permanent magnet) 을 재료의 축 방향과 평행하게 위치한다. 이 때, 영구자석은 재료의 축 방향으로만 이동 할 수 있으며 측정 대상체에 부착되어 타깃이 되기 때문에 커서(Cursor)라고도 불린다 [5,6].
자기변형 와이어의 한 쪽 끝에 펄스 전류를 인가하면 전류에 의한 원주 방향 자기장이 재료를 따라 진행하게 된다. 진행되는 원주 방향 자기장이 영구자석에 의한 축 방향의 자기장과 만나면 두 자기장의 합 벡터 방향으로 나선형 자기장이 유도되고 위드만 효과(Wiedemann effect)에 의해 재료는 순간적으로 비틀어지게 된다. 이때, 원주 방향 자기장은 제자리에 머물러 있는 것이 아니라 계속 재료를 따라 진행되기 때문에 두 자기장이 만나는 순간 재료가 비틀어지고, 원주 방향 자기장이 영구자석이 있는 지점을 벗어나면 재료는 다시 원상태로 되돌아 오게 된다. 이 시점, 즉 재료가 비틀어 졌다가 원상태로 돌아오는 순간에 초음파 중 하나인 비틀림 파(Torsional wave, T-wave)가 발생되는 것이다[7,8].
비틀림 파는 자기변형 와이어를 매질로 하여 영구자석을 기준으로 Fig. 1과 같이 양 방향으로 전파된다. 반사된 비틀림 파는 자기변형 와이어 한 쪽 끝에 위치한 센싱 코일(Sensing coil) 내부를 통과하여 지나가게 된다. 이 때, 비틀림 파는 자기변형 와이어에 일종의 외력으로 작용하므로 역자기변형효과에 의해 재료 자체의 투자율이 변화하는데 이 변화를 페러데이의 유도 전압 법칙에 의해 센싱 코일로 감지할 수 있게 되는 것이다.
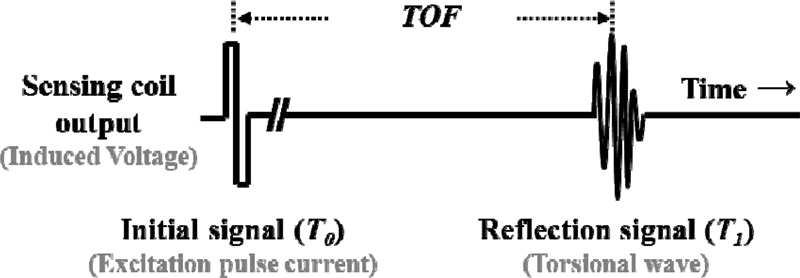
비틀림 파에 의한 센싱 코일의 출력 전압은 Fig. 2에 나타나있다. 펄스 형태의 전류에 의한 초기 신호(T0)와 반사지점에서 되돌아오는 초음파에 의한 수신 신호(T1) 사이의 시간 차이(Time-of-Flight, TOF)는 식(1)과 같이 표현 할 수 있다. 이 때, 두 신호에 대한 검출 시간 차이에 비틀림 파의 전파 속도(Propagation Speed, ν)를 곱하면 센싱 코일과 영구자석 사이의 거리(L)를 구할 수 있으며 이는 수식 (2)에 나타나 있다. 즉, 센싱 코일의 위치는 고정되어 있고, 일정한 주기를 갖는 펄스 전류를 자기변형 와이어의 한 쪽 끝에서 인가해 주기 때문에 첫 번째 신호가 검출 되는 지점을 기준으로 볼 수 있다.
영구자석은 자기변형 와이어를 따라 축 방향으로 이동이 가능하고, 이 위치에 따라 비틀림 파가 발생하는 지점 역시 달라지기 때문에 센싱 코일로 돌아오는 시간이 달라지게 되고 이에 따라 두 신호의 검출 시간 차이가 생기게 된다.
| (1) |
| (2) |
이 때, 초음파의 전파 속도는 온도의 함수로 온도에 따라 그 값이 변화하기 때문에 동일한 위치에서 초음파가 반사된다 하더라도 초음파의 전파 속도가 변화하는 만큼 전파 시간 역시 변화하게 된다. 따라서 TOF 역시 초음파 도파로의 온도에 의존적인 관계라고 할 수 있으며 이는 식(3)에 나타나 있다. 여기서 t 는 초음파 도파로의 온도이다.
온도 변화에 따른 초음파 수신 시간 차이(Difference for time-of-flight, DTOF) 값 변화는 상온에서의 초음파 수신 시간 차이(Time-of-flight at the room temperature, TOFR)를 기준으로 현재의 초음파 수신 시간 차이(Time of flight at the current temperature Room Temperature, TOFC) 사이의 관계로 나타낼 수 있으며 이는 식(4)와 같다.
| (3) |
| (4) |
따라서 이 온도 변화에 따라 측정된 TOFC는 상온에서의 TOFR과 비교해줌으로써 현재의 온도로 변환하는 방법을 이용해 초음파 도파로를 이용한 방식의 온도 측정이 가능할 뿐만 아니라 동일 위치에서 발생하는 DTOF만큼의 위치 오차를 유발할 수 있으므로 이에 대한 보상이 반드시 이루어져야 한다.
3. 자기변형 위치 센서의 온도 보상 알고리즘
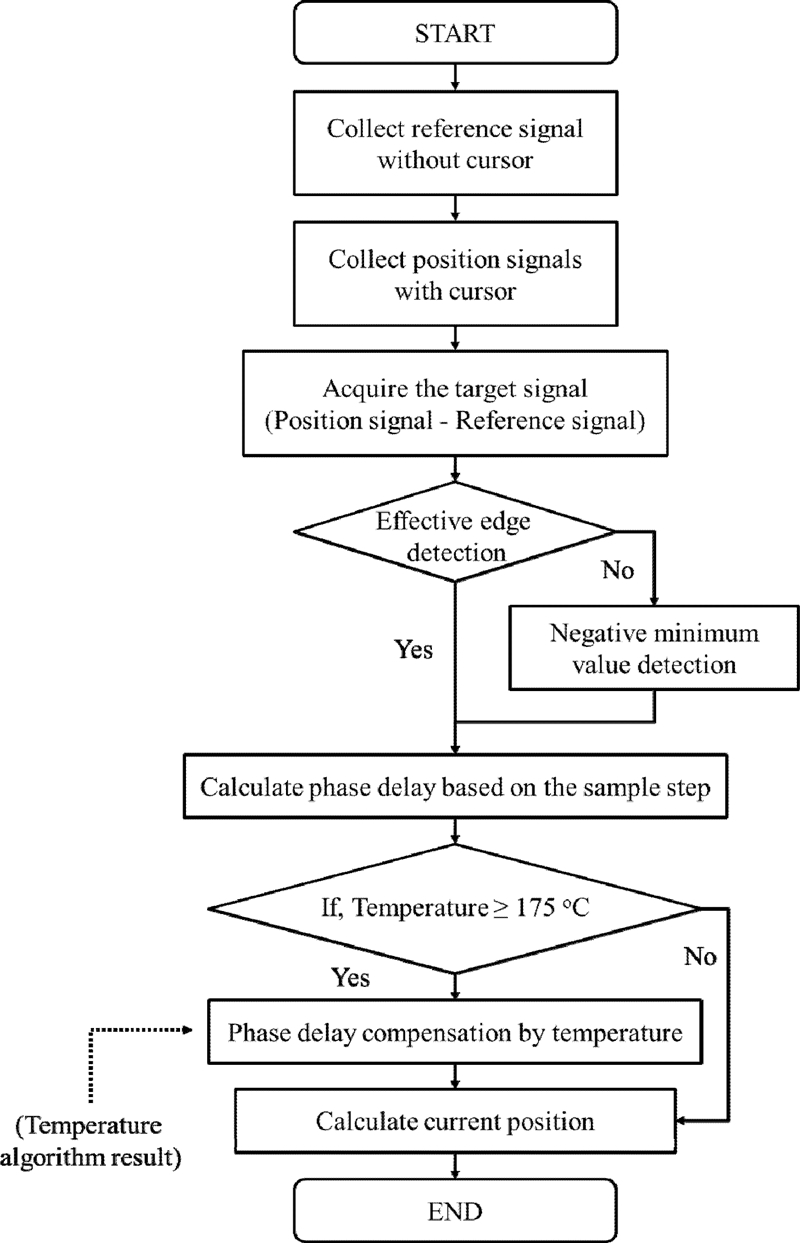
Fig. 3과 같이 자기변형 위치 센서의 온도 보상 알고리즘은 커서인 영구자석에 대한 위치 측정 알고리즘으로 시작한다. 자기 변형 와이어에 대한 온도 변화 역시 계속 계측하지만 실제로 해당 값을 직접적으로 활용하는 것은 큰 온도 변화에 의해 커서인 영구자석의 위치 측정 시, 오차를 발생하여 센서 자체의 성능에 영향을 미치는 상태이거나 전체 시스템 감시 측면에서 별도로 설정된 시스템 운영 조건을 넘어서는 상태로 시스템을 강제 종료해야 하는 상황인 경우라고 할 수 있다.
이에 자기변형 위치 센서의 온도 보상 알고리즘은 위치 측정을 주 알고리즘, 온도 측정을 부 알고리즘이 되도록 구성한다. 자기변형 와이어의 온도가 175 °C를 넘어서는 시점부터 온도 변화에 따른 유효 신호 지점 변동 추이가 실제 위치 측정에서 발생할 수 있는 오차 범위를 벗어나 직접적인 영향을 줌으로 175 °C 이상에서부터 온도 보상이 이루어지게 하였다[9].
Fig. 3의 알고리즘에서 커서인 영구자석 없이 인가 펄스 전류에 의한 신호(Reference signal)를 커서인 영구자석 위치에 따른 위치 신호(Position signal)에서 제거하여 커서인 영구자석의 위치 변화에 따라 바뀌는 대상 신호 (Target signal)를 추출한다. 또한, 대상 신호만을 추출함 으로써 커서인 영구자석에 대한 반사 신호가 수신 코일에 근접한 부분의 자기변형 와이어 끝 단에서 인가되는 인가 펄스 전류에 의한 초기 신호 영역에 들어와 중첩되면서 유효 신호 지점을 판별할 수 없는 불감대 영역이 발생하는 신호 적인 측면에 대한 원인을 줄일 수 있다.
대상 신호에 대한 위상 지연(Phase delay)을 커서인 영구 자석의 위치로 변환할 수 있다. 유효 신호 지점의 위상 지연을 계측하기 위해서는 신호 처리를 하는 부분에서 유효 신호가 무엇인지를 파악해야 하는데 이는 두 가지 방법으로 사용한다. 먼저 대상 신호는 커서인 영구자석에 의한 영향만 있으므로 대부분 위치와 상관없이 특정 형상을 가지는 파형이 있기 때문에 해당 파형의 가장자리(Edge) 특성을 설정해주고 해당 파형의 극값이 되는 지점을 유효 신호 지점으로 추출한다. 하지만 커서인 영구 자석이 0.1 m 이하인 지점에서는 앞선 특정 형상을 만족하는 파형이 아니라 보다 급격한 최솟값을 갖게 되어, 앞서 설정한 가장자리 특성을 만족하는 파형이 없는 경우 최솟값을 갖는 극점을 유효 신호 지점으로 추출할 수 있도록 하였다.
4. 온도 보상을 위한 자기변형 위치 센서 시스템
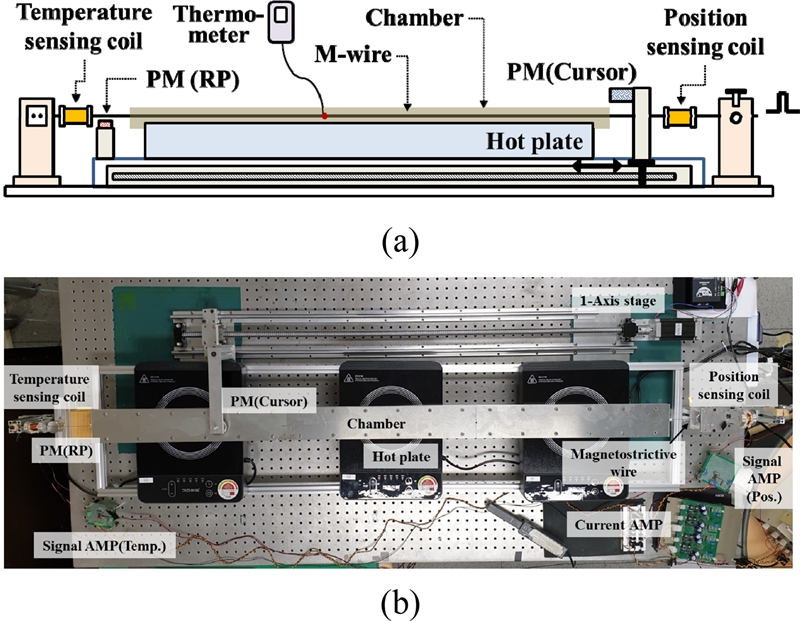
앞서 제안된 아이디어와 알고리즘을 토대로 온도 보상을 위한 자기변형 위치 센서 시스템을 Fig. 4와 같이 구축 하였다. Fig. 4 (a)는 구축된 시스템의 개략도이고, Fig. 4 (b)는 실제 구축된 시스템을 나타낸다. 먼저 자기변형 와이어의 양 단은 각각 와이어 고정 장치와 장력 조절 장치로 고정하였고, 자기변형 와이어의 온도 변화를 위해 열원을 위치 측정 전 구간에 일정한 간격으로 배치하였다. 이 때, 자기변형 와이어의 온도 변화를 일정하게 유지할 수 있도록 외부 챔버를 설치하였다.
챔버 내 자기변형 와이어의 온도를 측정하기 위해서 챔버 상단에 상용 디지털 서모미터의 프로브가 삽입될 수 있도록 작은 홈을 내어 내부에서 프로브의 끝 단과 자기변형 와이어가 체결 될 수 있도록 하였다. 위치 측정을 위한 커서인 영구자석은 단축 스테이지를 사용하여 챔버와 일정 간격을 유지한 상태로 자기변형 와이어의 축 방향을 따라 이동이 가능하도록 제작하였다. 온도 측정을 위한 영구자석은 반사지점(Reflection point, RP)으로 위치 이동 없이 온도 측정을 위한 센싱 코일로부터 일정거리 떨어진 곳에 고정되어 있다.
즉, 일정한 거리에 고정되어 있기 때문에 온도 측정을 위한 센싱 코일에서 얻어지는 유효 신호의 검출 시간 역시 고정되며 이 값이 바뀌는 것은 순수하게 자기변형 와이어의 온도에 의한 값이므로 이를 위치 측정 값 보상에 이용할 수 있게 되는 것이다. 위치 측정을 위한 센싱 코일은 인가 펄스 전류가 인가되는 지점인 장력 조절 장치 쪽에 온도 측정을 위한 수신 코일은 와이어 고정 장치 쪽에 배치되었고, 각 수신 코일에 대한 신호 증폭기도 동일한 형태로 제작하여 사용하였다.
온도 보상을 통한 정확도 향상 방법이 적용된 자기변형 위치센서의 검증을 위한 시스템 구성 조건은 Table 1에 나타나 있다. 자기변형 와이어는 직경 1 mm, 길이 1500 mm 의 자기변형 재료 중 하나인 Ni50Fe50을 사용하였다. 실제 온도 측정을 위한 센싱 코일과 반사지점인 영구자석이 배치된 곳은 위치 측정 시스템이 갖는 고유의 측정 불감대 영역이기 때문에 추가적인 자기변형 와이어 연장 없이 설치가 가능하다.
자기변형 와이어를 따라 이동하는 커서인 영구자석의 위치는 전체 위치 측정 범위 내에서 센싱 코일 출력이 솔레노이드 구조보다 안정적인 헬름홀츠 구조를 이용한 센싱 코일을 사용하였고[10-12], 자기변형 와이어의 온도 변화는 고정된 반사 지점인 영구자석을 사용하므로 솔레 노이드 구조를 이용한 수신 코일을 통해 측정하였다.
5. 자기변형 위치 센서의 검증
앞서 제안된 자기변형 위치 센서의 온도 보상을 위해 구축된 시스템과 알고리즘을 이용하여 온도 변화에 따라 발생하는 위치 오차에 대한 보상 검증을 수행하였다. 먼저 자기변형 위치 센서 자체의 성능 검증을 위해 실제 커서인 영구자석의 이동에 따라 대상이 되는 타깃의 위치를 측정할 수 있는지를 검증하기 위해 상온에서 커서인 영구자석을 0.1 m간격으로 이동시켜가며 그 결과를 확인하였다.
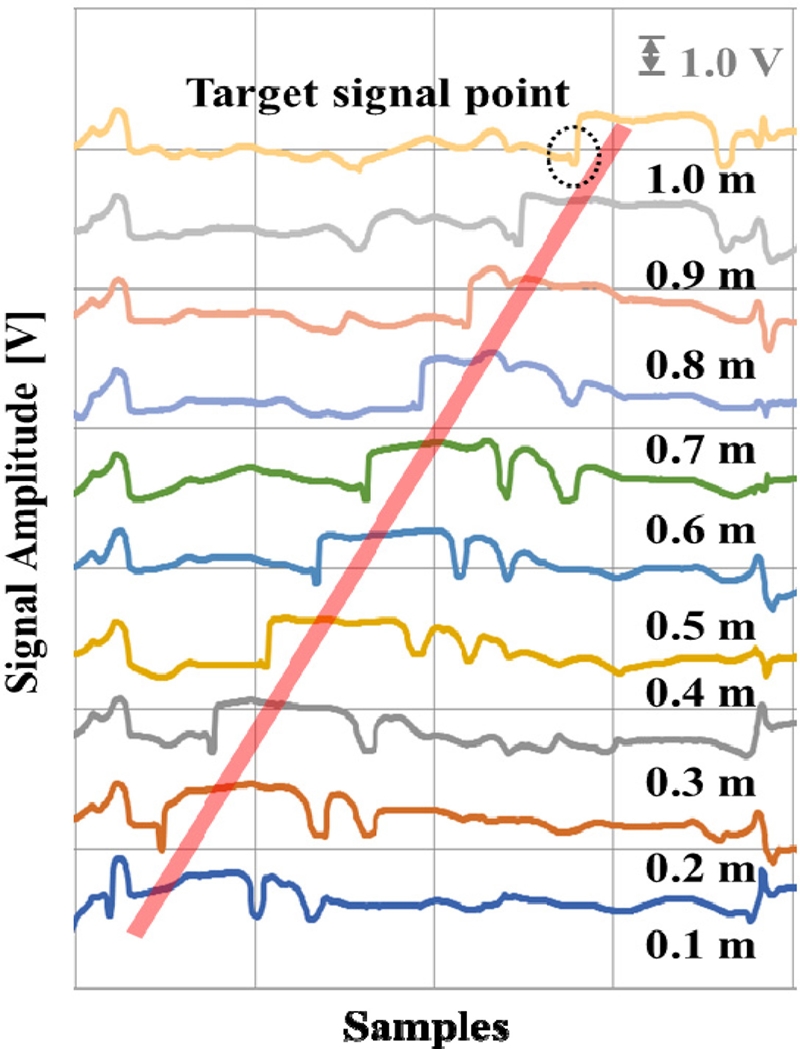
이를 토대로 커서인 영구자석을 최대 이동 가능 범위인 1.0 m인 지점에 고정한 뒤, 열원인 핫 플레이트를 이용해 자기변형 와이어의 온도를 올려가며 해당 지점에서의 위치 보상이 이루어지는지를 확인하였다. Fig 5는 커서인 영구자석을 0.1 m 간격으로 이동한 위치 변화에 따른 대상 신호의 변화를 하나의 그래프로 나타낸 것이다. 대상 신호에 표시된 부분이 유효 신호지점으로 알고리즘을 통해 해당 부분의 위상 지연을 측정함으로써 그 변화를 검출하고 이를 통해 커서인 영구자석의 위치를 측정할 수 있게 된다. 이 때, 커서인 영구자석이 0.1 m씩 이동할 때마다 검출 신호 내에서의 유효 신호가 검출되는 시간인 초음파 전파 시간은 평균 약 36 msec씩 선형적으로 증가하며 자기변형 와이어를 따라 이동하는 비틀림 파의 전파 속도는 약 2,778 m/sec이다.
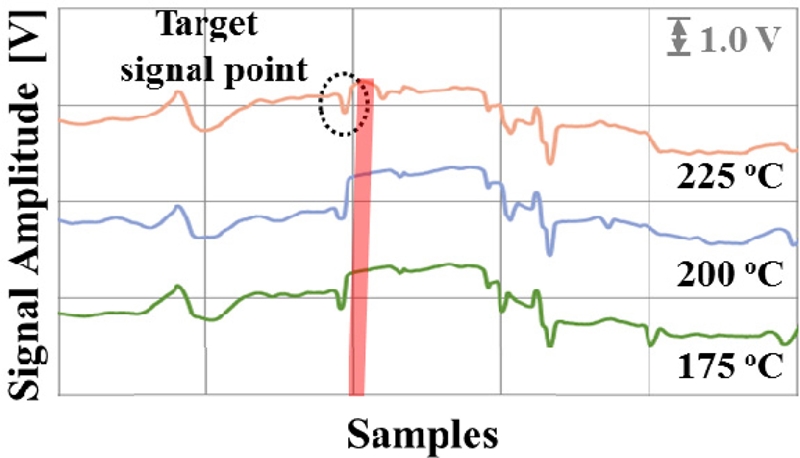
Fig. 6은 커서인 영구자석을 1.0 m인 지점에 고정한 뒤, 초음파 도파로인 자기변형 와이어의 온도를 변곡점인 175 °C부터 225 °C까지 변화하였을 때 위치 측정용 센싱 코일의 대상 신호를 온도 별로 나타낸 것이다. 자기변형 와이어의 온도 변화에 따라 고정된 커서인 영구자석의 위치에서 반사되어 돌아오는 유효 신호 지점이 변화하는 것을 확인 할 수 있다. 즉, 이러한 자기변형 와이어의 온도 변화에 따른 유효 신호 지점의 변화가 위치 측정 오차를 유발할 수 있는 것이다.
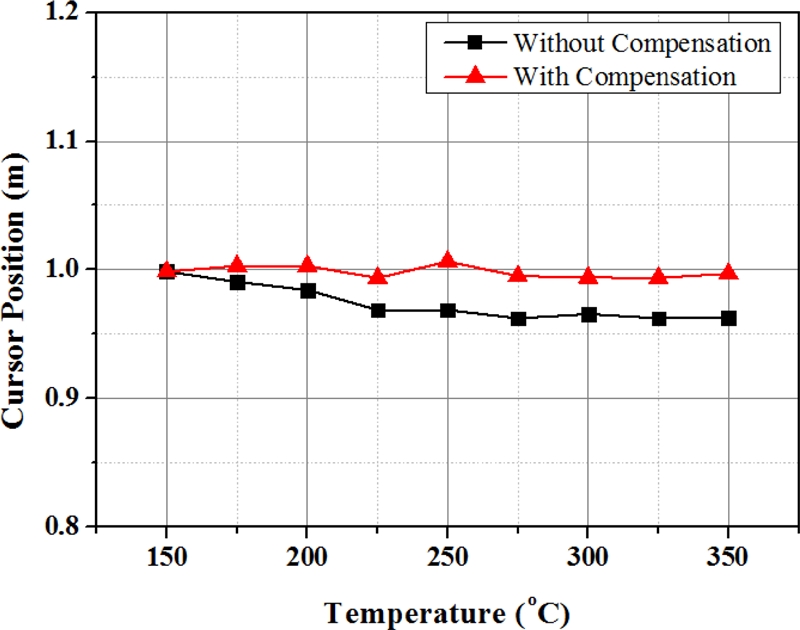
이에 본 논문에서 제안한 위치 측정 알고리즘으로 자기변형 와이어의 온도 변화에 따른 대상 신호 내 유효 신호 지점 변화의 보상 없이 위치가 계산된 결과와 온도에 대한 위상 지연으로 보상되어 위치가 계산된 결과를 Fig. 7과 Table 2에 함께 나타내었다. 커서인 영구자석이 위치 측정을 위한 센싱 코일로부터 1.0 m인 지점에 고정되어 있음에도 불구하고 자기변형 와이어의 온도가 175 °C를 넘어서는 시점부터 대상 신호 내 유효 신호 지점 변화 정도의 변곡점이 생기게 되고 이는 위치 측정에서 발생할 수 있는 오차 범위를 벗어나 보상이 필요한 수준 임을 알 수 있다. 이는 초음파 도파로인 자기변형 와이어를 따라 전파되는 초음파의 전파 속도가 온도가 올라가면서 느려지기 때문에 동일한 곳에 고정된 커서인 영구자석에서 반사되었다 하더라도 전파 시간이 달라져 오차가 유발되는 것이다.
이에 위치 및 온도에 대한 동시 측정 알고리즘 내 보상 온도조건을 만족하는 175 °C이상에서 온도 변화에 따른 초음파 전파 속도 변화에 대한 위상 지연 보상을 수행하였다. 실제 보상이 이루어지기 시작한 175 °C부터 최대 350 °C 까지의 모든 온도에 대한 평균 측정 오차는 보상 전 약 -29.272 m와 보상 후 약 -1.778 mm로 커서인 영구자석의 위치 측정 전 범위에 대해서 약 93.9% 수준으로 오차를 감소시켰음을 확인하였다.
6. 결 론
초음파 도파로를 이용한 위치 및 온도 측정은 유사 원리로 동작하기 때문에 그 특성에 맞게 일부가 변형된 구조를 가지지만 이를 결합한 단일 시스템 측면에서의 연구는 아직 시작 단계이다. 위치 측정 방법이 더 넓은 산업 분야나 더 다양한 작업 환경으로 적용되기 위해서는 이러한 온도와 같은 주변 환경에 대한 위치 측정의 보상이 반드시 필요하다.
본 연구에서 제안된 방법은 위치 측정에 대한 보상이 필요할 때, 별도의 장치를 추가적으로 사용하는 것이 아니라 기존 시스템을 활용하여 하나의 시스템으로 위치와 온도의 두 물리량을 측정하고 그 결과를 유기적으로 활용하여 보상할 수 있는 장점을 가지고 있다.
제안된 시스템은 별도의 추가 장치 없이 자기변형원리를 이용한 초음파 방식의 위치 측정 시스템의 구조에서 오는 측정 불감대 영역을 활용하여 하나의 시스템으로 측정하고자 하는 대상에 부착되어 움직이는 커서인 영구자석의 위치와 초음파 도파로인 자기변형 와이어의 온도를 동시에 측정할 수 있는 구조이다. 통합된 시스템에 적용하기 위해 제안된 알고리즘은 측정 하고자 하는 대상에 부착되어 이동하는 커서인 영구자석의 위치를 측정하는 주 알고리즘과 초음파 도파로인 자기변형 와이어의 온도를 측정하는 부 알고리즘을 기반으로 한다.
본 연구를 통해 제안된 방법은 수신 코일이 추가되면서 일부 수신 코일 자체의 구조가 변경되긴 하지만 전체적인 위치 측정 시스템이 자체적으로 가지는 불감대 영역을 활용하기 때문에 온도 측정을 동시에 수행하기 위한 구조적인 확장이나 추가 공간을 별도로 요구하지 않으며 단일 장치로 두 개의 물리량을 측정할 수 있다는 것에 그 의미가 있다.
또한, 위치와 온도 측정을 위한 두 알고리즘의 유기적인 데이터 활용을 통한 측정 위치에 대한 온도 보상 통합 알고리즘을 제안하였고 온도 보상 단계에서 약 93.9%의 오차 감소 효과를 확인하였다. 제안된 방법은 위치와 온도 두 물리량에 대한 측정이 유사한 원리를 가지고 단일 시스템 내에서 이루어 진다는 측면에서 시스템을 자체적으로 상태를 감시하는 목적으로도 활용 할 수 있다. 대부분의 시스템에 문제가 발생하는 경우는 급격한 온도 변화를 동반하는데 주로 온도 상승을 야기한다. 따라서 시스템의 노후화나 결함 등의 이유로 시스템에 과부화가 걸려 온도가 급격하게 상승하는 경우, 이를 감지할 수 있으므로 시스템의 강제 종료나 점검이 필요한 시점을 알려주는 시스템 상태 감시를 할 수 있다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술 평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20161520101300). 또한, 이 논문은 2016년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 지역신산업선도인력양성사업 성과입니다. (No. 2016H1D5A1910991)
References
- http://www.mtssensors.com/fileadmin/media/pdfs/551019.pdf (retrieved on Nov. 19, 2019).
-
D. Zhang, Z. Zhou, J. Sun, E. Zhang, Y. Yang, and M. Zhao, “A Magnetostrictive Guided-Wave Nondestruc-tive Testing Method With Multi-Frequency Excitation Pulse Signal”, IEEE Trans. Instrum. Meas., Vol. 63, No. 12, pp. 3058-3066, 2014.
[https://doi.org/10.1109/TIM.2014.2324812]

-
Y. Hatsukade, T. Kobayashi, S. Nakaie, N. Masutani, and Y. Tanaka, “Novel Remote NDE Technique for Pipes Combining HTS-SQUID and Ultrasonic Guided Wave”, IEEE Trans. Appl. Supercond., Vol. 27, No. 4, pp. 1-4, 2017.
[https://doi.org/10.1109/TASC.2016.2631421]

-
M. R. Karafi, Y. Hojjat, and F. Sassani, “A New Hybrid Longitudinal-Torsional Magnetostrictive Ultrasonic Transducer”, Smart. Mater. Struct., Vol. 22, No. 6, pp. 1-7, 2013.
[https://doi.org/10.1088/0964-1726/22/6/065013]

- E. J. Yoo, M. D. Noh, and Y. W. Park, “Development of Magnetostrictive Position Sensor Based on Ultrasonic Wave”, Proc. of KSPE. Conf, pp. 974-974, Jeju, Republic of Korea, 2018.
- E. J. Yoo, M. D. Noh, H. G. Lee, and Y. W. Park, “Characterization of Magnetostrictive Position Sensor Based on Non-Contact Ultrasonic Wave”, Proc. of KSPE Conf, pp. 709-709, Gwangju, Republic of Korea, 2017.
-
N. S. Tzannes., “Joule and Wiedemann Effect–The Simultaneous Generation of Longitudinal and Torsional Stress Pulses in Magnetostrictive Materials”, IEEE Trans. Sonics Ultrason., Vol. SU-13, No. 2, pp. 33-41, 1966.
[https://doi.org/10.1109/T-SU.1966.29373]

-
E. J. Yoo, Y. W. Park, and M. D. Noh, “Development of Magnetostrictive Control Rod Position Indicator”, J. Korean Soc. Precis. Eng., Vol. 34, No. 12, pp. 889-895, 2017.
[https://doi.org/10.7736/KSPE.2017.34.12.889]

- E. J. Yoo, Y. W. Park, and M. D. Noh, “Feasibility of Ultrasonic Temperature Sensor Based on Magnetostrictive Principles”, Proc. Am. Nucl. Soc. Winter Meet. Expo, Fuel Cycle Waste Manag. General-II, PP. 301-302, Orlando, United States of America, 2018.
-
V. Rokhlin, “Diagonal Forms of Translation Operators for the Helmholtz Equation in Three Dimensions”, Appl. Comput. Harmon. Anal., Vol. 1, No. 1, PP. 82-93, 1993.
[https://doi.org/10.1006/acha.1993.1006]

-
H. C. Choi, J. H. Choi, G. H. Jang, J. O. Park, and S. H. Park, “Two-Dimensional Actuation of a Microrobot with a Stationary Two-Pair Coil System”, Smart. Mater. Struct., Vol. 18, No. 5, pp. 1-9, 2009.
[https://doi.org/10.1088/0964-1726/18/5/055007]

- E. J. Yoo, Y. W. Park, and M. D. Noh, “Characterization of Magnetostrictive Position Sensor for Helmholtz Coil Geometric Conditions”, Proc. of KSPE Conf, pp. 149-149, Yeosu, Republic of Korea, 2016.