비파괴 지능형 과일 당도 자동 측정 시스템 구현
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recently, the need for IoT-based intelligent systems is increasing in various fields. In this study, we implemented the system that automatically measures the sugar content of fruits without damage to fruit's marketability using near-infrared radiation and machine learning. The spectrums were measured several times by passing a broadband near-infrared light through a fruit, and the average value for them was used as the input raw data of the machine-learned DNN(Deep Neural Network). Using this system, he sugar content value of fruits could be predicted within 5 s, and the prediction accuracy was about 93.86%. The proposed non-destructive sugar content measurement system can predict a relatively accurate sugar content value within a short period of time, so it is considered to have sufficient potential for practical use.
Keywords:
Near infrared, Spectrometer, Deep Neural Network, Brix(Sugar Content), LabVIEW1. 서 론
농림축산식품부가 펴낸 ‘2018 양정 자료’ 에 따르면 2017년 국내 잠정 식량자급률은 48.9%이다. 국민 식량의 절반 이상이수입으로 충당되고 있으며[1], 식량자급률이 꾸준히 하락세를 보이고 있다. 그 원인은 급격히 빨라지고 있는 고령화 사회 구조는 물론 농촌 인구의 감소에 따른다. 이로 인하여 농산물 재배의 어려움이 따르고 있으며 농가 소득이 꾸준히 감소되고 있다. 이에 정부와 기업은 큰 문제로 떠오르고 있는 농촌 문제를 해결하기 위하여 새로운 4차 산업혁명 기술을 농업 제반 분야에 적용하여 근본적인 해결책을 제시하고자 하는데, 이를 ‘스마트팜(Smart Farm)’이라고 부른다.
스마트 팜이 다루는 많은 분야 중에서 과일의 등급 분류 자동화 기술은 매우 중요한 분야의 하나로서 많은 관심을 받고 있다. 과일의 등급 분류 시 무게, 크기, 당도 등 과일의 품질에 영향을 주는 여러 요소들이 있지만 소비자들이 가장 중요하게 생각하는 것은 과일의 당도이다. 한편 기존에는 당도 측정을 위하여 과일의 표면을 훼손하여 추출한 과즙을 당도계에 넣어 측정하거나 또는 전문가의 경험에 의존하는 등 수동적인 방법을 사용하고 있다. 이로 인하여 과일이 훼손되거나 많은 인력과 시간이 소요되는 문제점이 따른다.
따라서 본 논문에서는 과일 선별 과정에서 꼭 필요하면서도 수동으로만 수행되던 당도 판정 과정을 자동화하고자 한다. 즉 과일을 훼손하지 않고 자동으로 당도를 측정하는 비파괴 지능형 당도 자동 측정 시스템을 구현하였다. 구현된 기술을 통하여 빠르고 쉽게 그리고 정확하게 당도 측정이 가능한 것을 실험적으로 확인하였다. 그 뿐만 아니라 측정 과정에서 과일이 훼손될 염려가 없기 때문에 품질 상태를 그대로 유지할 수 있다는 장점이 있다. 기술 구현을 위하여 PC 기반의 제어 계측 프로그램인 LabVIEW를 사용하였으며 당도 판정 과정은 기계학습을 통하여 이루어진다. 모든 과정의 자동화 및 실시간 모니터링이 가능하므로 일반인도 어려움 없이 사용 가능할 것으로 사료된다.
과일의 당도를 측정하기 위하여 광대역 근적외선 광원 및 분광기를 사용하여 측정된 투과 스펙트럼 데이터를 DNN(Deep Neural Network)이라는 기계학습(Machine Learning)의 입력 데이터로 사용하여 당도 값을 예측하였다. 구현 과정에서 사용된알고리즘과 기술들에 대해서는 아래의 목차들을 통하여 자세히 설명하도록 하겠다.
2. 사용 프로그램 및 관련 이론
2.1 LabVIEW
LabVIEW는 Laboratory Virtual Instrument Engineering Workbench를 줄인 말이다. 이것은 마이크로소프트 윈도우즈, 애플 매킨토시, 선 스파이크스테이션을 이용하는 PC에서 운영될 수 있으며 강력하고 유연성 있는 해석 소프트웨어 시스템의 일종이다. LabVIEW는 여러 범용의 C 또는 BASIC 개발 시스템 처럼 프로그램 개발 도구이다. 다른 프로그래밍 시스템들이 코드를 생성하기 위하여 텍스트 기반의 언어를 사용하는 데 반하여 LabVIEW는 여러 가지 문법적인 사항들을 없애고 블록 다이어그램이라 불리는 흐름도를 사용하여 프로그램을 생성하는데, 우리는 이 언어를 그래피컬 프로그래밍이라고 부르며 간단히 G 언어라고 한다[2].
2.2 Machine Learning
기계학습(Machine Learning)은 경험적 데이터를 통하여 학습하고 이를 바탕으로 예측을 탐구하여 스스로 성능을 발전시키는 시스템과 이를 위한 알고리즘을 연구하고 구축하는 기술이다[3][4][5].
기계학습은 미리 학습된 알고리즘에 측정 데이터(Input)를 입력하였을 때 입력 데이터의 실제 목표 값(Target)과 출력 데이터(Output) 간의 오차를 최소화하는 것이 매우 중요하다. 이를 위해서는 사전 학습 과정을 통하여 출력 데이터를 계산하는데 적용되는 최적의 가중치 데이터(Weight)를 추출하는 것이 매우 중요하다. 현재까지 최적의 가중치 데이터 값을 얻기 위한 많은 기계학습 알고리즘들이 제시되어 왔으며 이에 대한 연구가 계속 진행 중이다.
본 논문에서는 과일의 당도 추정을 위하여 기계학습 알고리즘 중 하나인 DNN(Deep Neural Network)을 사용하였다. 실험을 통하여 약 81%의 과일이 10% 이내의 오차 범위, 17%의 과일이 20% 이내의 오차 범위, 그리고 2%의 과일이 20% 이상의 오차 범위를 가지고 결과를 얻었다. 아래에서 DNN(Deep Neural Network)에 대하여 소개하도록 하겠다.
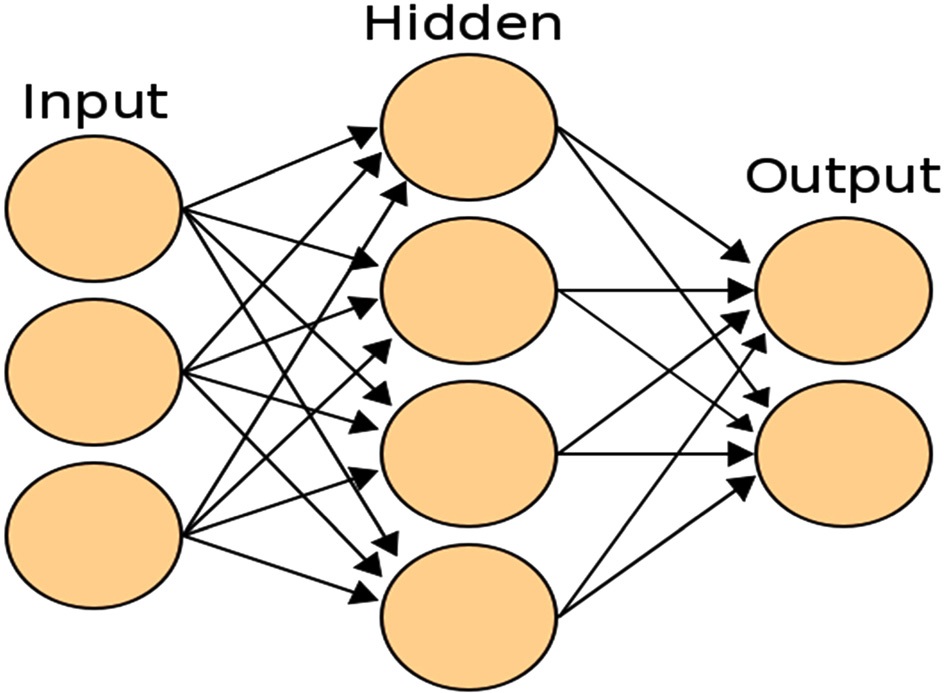
신경망은 인간이 뇌를 통해 문제를 처리하는 방법과 비슷하게 문제를 해결하기 위해 채택한 구조이다. 인간의 뇌에서 구조조직인 뉴런(neuron)과 뉴런이 연결되어 일을 처리하는 것처럼, 수학적 모델로의 뉴런이 상호 연결되어 네트워크를 형성할 때 이를 신경망이라 한다. 이를 생물학적인 신경망과 구별하여 인공 신경망(Artificial Neural Network)이라고도 한다. 신경망에서는 각 뉴런이 독립적으로 동작하는 처리기의 역할을 하기 때문에 병렬성(Parallelism)이 뛰어나고, 많은 연결선에 정보가 분산되어 있다. 따라서 몇몇 뉴런에 문제가 발생하더라도 전체 시스템에 큰 영향을 주지 않는 결함 허용(fault tolerance) 능력이 있으며, 주어진 환경에 대한 학습 능력이 있다. 이러한 특성은 인공 지능에 이용되고 있으며, 문자 인식, 화상 처리, 자연 언어처리, 그리고 음성 인식 등 여러 분야에서 이용되고 있다[6].
Fig. 1은 인공 신경망(Artificial Neural Network, 이하 ANN)을 보여주고 있다. 앞에서 기계학습은 입력 데이터가 들어왔을 때 입력 데이터의 실제 목표 값과 출력 데이터 간의 오차 범위를 최소화할 수 있도록 가중치 데이터 최적의 값을 구하는 것이 궁극적인 목표라고 하였다. Fig. 1을 보면 Input이 입력 데이터로 주어질 때 중간 레이어(Layer)인 Hidden은 그 입력 데이터에 대한 출력 데이터가 된다. 그리고 다시 Hidden은 입력 데이터가 되고 Output은 최종 출력 데이터가 된다. 이때 최종 출력 데이터인 Output과 실제 목표 값의 차를 최소화하기 위하여는 기계학습을 통하여 최적의 가중치 데이터를 구하는 것이 필요하다. Fig. 1에서 가중치 데이터는 각각의 층을 연결하는 선으로서 각 층의 노드에 얼마만큼의 비중을 두는지를 결정하게 된다. 이 연산관계는 아래와 같은 합성함수를 생각하면 이해하기 쉽다. 합성함수란 두 함수를 합성하여 얻은 함수[7]로서 아래의 수식으로 표현될 수 있다.
| (1) |
| (2) |
| (3) |
여기서 X는 Input, H는 Hidden, Y는 Output을 나타낸다. Fig. 1의 연산관계를 수식으로 표현하면 아래의 관계로 표현된다.
| (4) |
| (5) |
W는 Weight, b는 Bias로서 신경망이 편향된 정도를 나타내고 있다. 그리고 k는 Input의 k 번째 순서 노드를 나타내고, j는 Hidden의 j 번째 순서 노드를 나타내며, i는 Output의 i 번째 순서 노드는 나타낸다. Input은 N 개의 노드로 구성되며, Hidden은 M 개의 노드로 구성된다.
수식을 간단하게 풀이하면 모든 Input 노드 층과 가중치 데이터가 곱해진 값을 전부 합친 다음 그 결과값에 편향 정도를 나타내는 Bias 값을 더해준다. 해당 과정을 통하여 Hidden의 모든 노드 층에 대하여 값이 결정되면 다시 Input에서 진행하였던 절차를 진행하여 Output를 구하면 된다.
Fig. 1은 Hidden 레이어가 하나만 있는 ANN을 나타낸다. 그러나 더 많은 Hidden 레이어를 사용함으로써 더욱 높은 정확도를 얻을 수 있는데 이를 DNN(Deep Neural Network)이라고 한다. 하지만 DNN(Deep Neural Network)의 경우 ANN보다 많은 양의 연산양을 필요로 하기 때문에 더 많은 메모리와 시간을 필요로 한다는 단점이 있다. 또한 레이어가 많아진다고 해서 정확도가 항상 더 높게 나온다는 것을 기대하기 어려운 점도 있다. 이는 레이어가 많아지는 것(깊어짐)에 따라 가중치 데이터의 효과가 희미해질 수 있고 결국에는 값이 소멸되는 현상(Vanishing Gradient)이 일어나게 되어 학습이 이루어지지 않은 결과를 초래할 수 있다. 따라서 DNN(Deep Neural Network)을 적용할 때에는 학습이 잘 이루어지는 최적의 레이어 개수를 추출할 필요가 있고 본 논문에서는 3 레이어를 사용하였다. 여기서 레이어는 Hidden와 첫 입력층의 개수이다.
Fig. 2는 본 논문에서 사용된 DNN(Deep Neural Network)을 보여준다.
기계학습은 입력 데이터를 인가하여 얻어진 출력 데이터와 입력 데이터의 실제 목표 값 간의 오차를 최소화하는 최적의 가중치 데이터를 확보하는 과정이다. 이때 학습을 진행하면서 가중치 데이터는 계속해서 갱신되고 이에 따라 오차는 점점 작아지는데 이때 오차를 계산하는 방법 중의 하나가 평균제곱오차(Mean Square Error, 이하 MSE)이다.
MSE를 간단하게 설명하면 측정값 또는 예측 값과 목표 값 간의 차의 제곱을 계산할 때 이들의 평균값[8]을 의미한다.
MSE를 이용하여 출력 데이터와 목표 값의 오차를 구하는 수식은 아래와 같다.
| (6) |
Target는 목표 값을 나타내고 Y는 Output을 나타낸다. 모든 노드에 대해서 Target과 Y의 차의 제곱 값들을 구한 뒤 이들의 평균 값이 비용함수(Cost)이며, 가중치 데이터 갱신을 위해 필요한 값이다.
가중치 데이터의 갱신을 위해서는 아래의 수식이 사용된다.
| (7) |
갱신하려는 새로운 가중치 데이터는 이전의 가중치 데이터에서의 비용함수를 이전 가중치 데이터로 미분한 값을 학습 속도(Learning Rate)와 곱한 뒤 이를 이전의 가중치 데이터로부터 빼는 것으로 표현된다. 한편 최적의 학습 상태에서는 갱신된 가중치 데이터와 이전의 가중치 데이터가 거의 같은 값을 보인다. 이는 수식 (7)에서 미분 값이 0이 되는 것을 의미한다. 비용함수는 (Target – Y)의 제곱으로 구해지는데 Y는 가중치 데이터와 입력 데이터를 곱하여 나온 결과이므로 Y의 제곱 과정에서 가중치 데이터가 제곱이 된다. 이로부터 비용함수는 가중치 데이터에 대한 이차함수로 주어진 다는 것을 알 수 있다. 따라서 비용함수를 가중치 데이터로 미분한 값을 0으로 만드는 가중치 데이터가 최적의 가중치 데이터가 되며 이 값에서 비용함수 즉 오차 범위가 최소가 된다. 수식 (7)에서는 미분 값이 0이 되는 위치까지 얼마만큼 빠르게 도달하는 가를 결정하며, 값이 클수록 빠르게 도달하지만 최솟값 지점의 정확성에 영향을 미친다.
3. 실험 방법
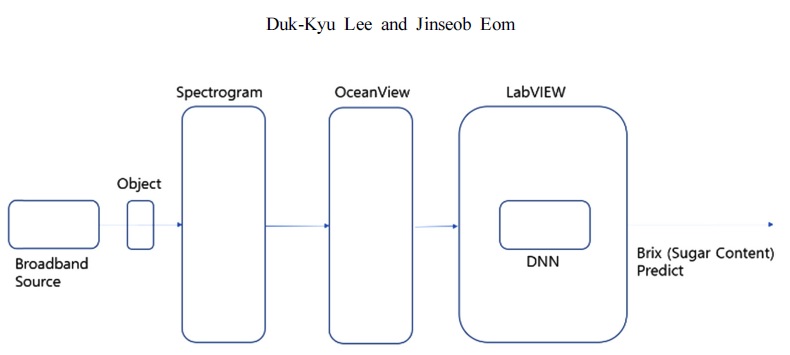
본 논문에서 구현된 비파괴 지능형 당도 자동 측정 시스템의 구성도를 Fig. 3에 보였다. 먼저 넓은 파장 대역을 가지고 있는 광원(Broadband Source)으로부터 출력된 광이 피사체(Object)에 입사되고 피사체를 투과한 광이 분광기(Spectrometer)에 입력된다. 다음으로 분광기의 출력 스펙트럼 데이터를 저장하고 있는 OceanView 프로그램으로부터 LabVIEW 프로그램으로 피사체의 투과 스펙트럼 데이터가 전달된다. LabVIEW 프로그램에서는 전달된 투과 스펙트럼 데이터에 대하여 DNN(Deep Neural Network)을 적용하고 예측된 피사체의 당도를 모니터에 보여준다.
실험에서 당도 측정 대상 과일로서는 상대적으로 구하기가 쉽고 광의 투과성이 좋은 방울토마토를 선택하였다. 일반적으로 방울토마토의 투과 대역은 400~1100 nm의 영역이다. 광원으로는 700~2500 nm의 넓은 근적외선 대역을 가지는 할로겐 램프를 사용하였으며 광섬유를 통하여 출력된 광을 방울토마토에 조사했다. 따라서 방울토마토를 투과한 광의 파장 대역은 대략700~1100 nm이며 이는 다시 분광계에 입사된다. 분광기는 400~1100 nm 구간의 스펙트럼을 보이도록 설정되었으며 측정된 스펙트럼의 한 예를 Fig. 4에 보였다(Fig. 4는 Ocean Insight 분광기와 함께 사용되는 디스플레이 프로그램인 OceanView를 통하여 보인 스펙트럼이다. 400~700 nm의 값은 주변의 환경 요인에 의한 것이다).
일반적으로 방울토마토의 당도가 높으면 입사된 근적외선 광의 대부분은 내부에서 흡수되고 소량의 광 만이 투과된다. 반대로 당도가 낮을 때에는 많은 양의 근적외선이 투과된다. 근적외선 광을 과일에 조사하면 과일 속에 포함하고 있는 당도 성분과 반응하게 되는데, 이때 당도와 관련된 근적외선 파장이 흡수되는 양이 많을 경우 당도가 높다고 할 수 있고, 적으면 당도가 낮다고 할 수 있기 때문이다(흡수되는 양이 많다는 것은 투과되는 양이 적다는 뜻이다). 따라서 당도가 높을 때는 스펙트럼의 높이가 낮아지고 당도가 낮을 때는 스펙트럼의 높이가 커진다. 즉 스펙트럼의 높낮이는 광도의 변화를 나타내며, 스펙트럼의 전체적인 분포는 변하지 않는다.
Fig. 4에서 보인 스펙트럼의 x축은 파장을 나타내고, y 축은 광의 세기를 나타낸다. 본 논문에서는 x축 구간인 400~1100 nm의 700 nm 파장 대역을 2048개의 포인트로 세분화하여 각각에 해당하는 y축 값을 기계학습을 위한 학습 데이터로 사용하였다.
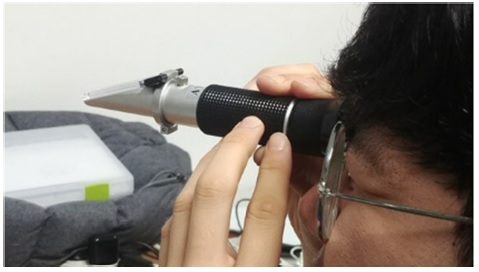
학습을 진행하기에 앞서 학습 데이터에 대한 목표 값(Target)이 필요하기 때문에 굴절 당도계를 사용하여 방울토마토의 당도를 측정(파괴 당도 측정) 하였고 이를 목표 값으로 선정하였다(측정된 방울토마토의 당도는 약 5~7 Brix 이었다.) 굴절 당도계를 사용한 당도 측정 과정을 Fig. 5에 나타냈다.
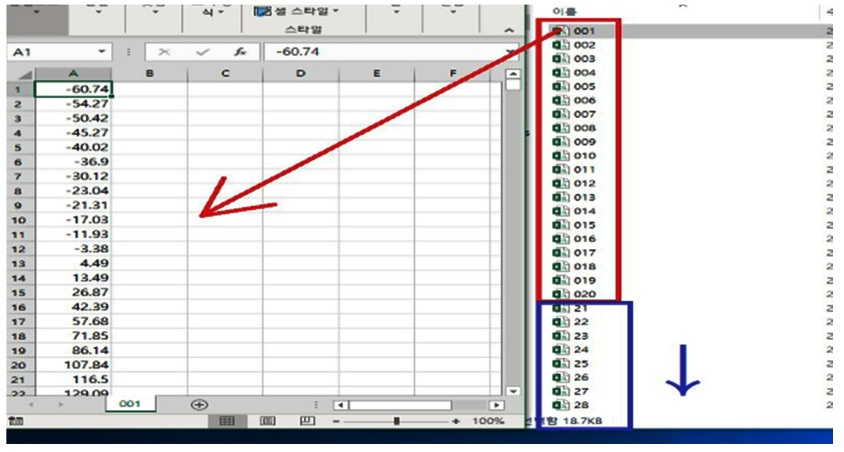
이제 학습을 시작하는 과정에서 부딪힌 문제점은 과일의 경우 과육 내부 상태가 균일하지 않기 때문에 광의 입사 방향에 따라 당도가 조금씩 달라진다는 점이다. 이를 해결하기 위해 실험에서는 분광기 앞에 놓인 방울토마토를 1초 동안 일정한 패턴으로 지그재그 회전시키면서 20개 부위의 투과 스펙트럼을 얻었다. 그리고 LabVIEW 프로그램에서 이들의 평균 스펙트럼을 구하여 학습용 및 테스트용 입력 데이터로 사용하였다. 이를 통하여 방울토마토의 부위별 당도 차이 가능성 문제점을 최소화 할 수 있었다. LabVIEW 프로그램에서 평균 스펙트럼을 구하는 과정을 Fig. 6에 보였다. 빨간색으로 표시된 우측 박스 내부를 보면 csv 파일이 1번부터 20번까지 모여 있는 것을 확인할 수 있고 각 csv 파일은 2048개의 광의 세기 값으로 구성된다. 주어진 방울토마토에 대한 20개의 스펙트럼 측정이 완료되면 파란색으로 표시된 우측 박스에서 보인 것처럼 다음 순서의 방울토마토에 대한 20개의 csv 파일이 21번부터 40번까지 쌓이는 순서로 진행된다. 이 과정에서 방울토마토의 꼭지 부위에서는 상이한 스펙트럼이 측정되며 이는 평균을 구하는 과정에서 큰 오차를 야기할 수 있으므로 이 스펙트럼을 제거하는 것이 필요하다. 이를 위하여 20개 스펙트럼의 평균을 구한 뒤 각각의 스펙트럼과 평균 스펙트럼 간의 차를 계산하여 임계 값 이상을 보이는 스펙트럼은 재 평균 계산 과정에서 제외했다.
DNN(Deep Neural Network)은 입력에 2048개의 입력 노드, 첫 번째 Hidden 레이어에 20개 노드, 두 번째 Hidden 레이어에 10개 노드, 그리고 출력은 1개 노드로 구성된다. 각 Hidden 레이어 노드 20개와 10개의 노드에 입력되는 값은 이전 노드에서 가중치와 계산되어 출력된 값 들이다.
2048개의 입력 노드 값으로 평균 스펙트럼의 2048개 값이 사용된다. Bias 값은 0, 얻어진 Weight 값은 [2048 × 20], [20 × 10], [10 × 1]의 크기로 각각 실수 값을 가진다. Learning Rate ρ의 값은 각각의 레이어에서 모두 10-9의 값을 사용하였다.
Fig. 7은 구현된 비파괴 지능형 당도 측정 시스템의 전체적인 하드웨어를 보여준다. 방울토마토가 컨베이어 벨트를 통하여 광원과 분광기의 중간 위치에 놓이게 되면 회전판을 통하여 방울토마토는 회전된다. 이 동안에 방울토마토를 투과한 광은 분광기로 입사되어 스펙트럼 데이터를 형성한다. LabVIEW 프로그램에서는 20개의 스펙트럼에 대한 평균 스펙트럼 데이터를 계산하고 이를 DNN(Deep Neural Network)을 위한 입력 데이터로 사용하여 해당 과일의 당도를 예측할 수 있다.
4. 실험 결과
4.1 데이터셋 준비
Fig. 6에서 보인 것처럼 데이터 셋으로서 한 개의 방울토마토에 대하여 20개의 부위별 스펙트럼 csv를 만들었다. 그리고 이들의 스펙트럼 평균을 구하여 부위별 당도 차이 가능성으로 인한 판정 오류를 최소화하였다. 특히 꼭지 부위 투과 시에 얻어질 수 있는 상이한 스펙트럼을 제외한 후에 다시 평균을 구하여 학습 데이터로 사용하였다. 학습을 진행하기 위하여 500개의 방울토마토로부터 500개의 학습 데이터를 마련하였고 학습된 결과를 테스트하기 위하여 방울토마토 286개의 데이터를 테스트 데이터로 사용하였다. 학습 횟수는 약 5천만 회로서, 학습 횟수 1회는 학습 데이터 500개를 모두 사용하여 학습하였음을 의미한다. 학습 데이터용과 테스트 데이터용을 위한 총 786개의 방울 토마토에 대한 목표 값을 설정했고 위에서 설명했듯이 그중 500개의 데이터는 학습 데이터로 사용하였다.
4.2 학습 결과 검증
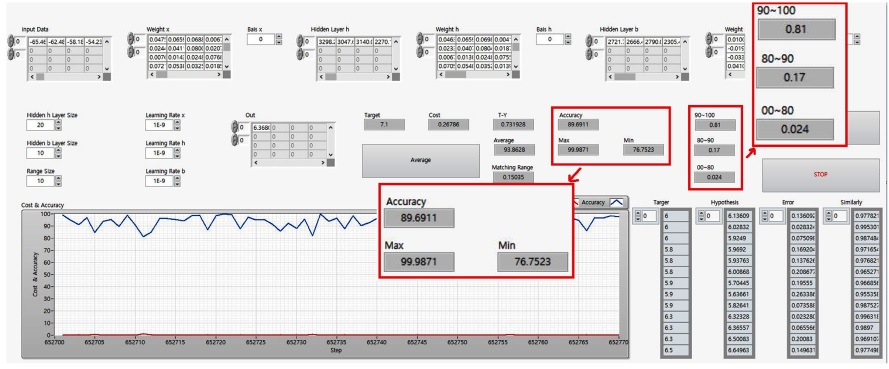
500개의 학습 데이터를 사용하여 확보된 학습 모델(즉 Weight)에 286개의 테스트 데이터를 적용한 결과를 Fig. 8에 보였다. Fig. 8의 하단에서 보인 Cost & Accuracy 그래프에서 빨간 곡선은 Cost(비용), 파란 곡선은 Accuracy(정확도)를 나타낸다. 비용은 테스트 데이터에 대한 목표 값과 출력 값의 차를 제곱한 값이고 정확도는 목표 값과 출력 값의 근사 정도를 나타내는 수치이다. 예를 들어 테스트 데이터의 목표 값이 6.0 Brix이고 출력 값이 5.4 Brix이라면 비용은 6.0-5.4의 제곱인 0.36이며 정확도는 5.4/6.0인 90%라고 할 수 있다. Fig. 8에서 비용은 0에 근접하고 있으며 정확도는 100에 근접하고 있는 것을 확인할 수 있다. 286개의 방울토마토 중에서 가장 높은 정확도는 약 99.987%이고 가장 낮은 정확도는 약 76.752%이었으며 전체 평균 정확도는 약 93.86%이었다.
Table 1은 286개의 테스트 데이터를 사용하여 학습이 잘 되었는지를 검증한 뒤 정확도를 구간별로 나누어 정리한 것이다. 즉 90~100%의 정확도를 가지는 방울토마토의 수량은 232개이며 이는 전체의 약 81%에 해당한다.
4.3 당도 예측 실험 및 추후 개선점
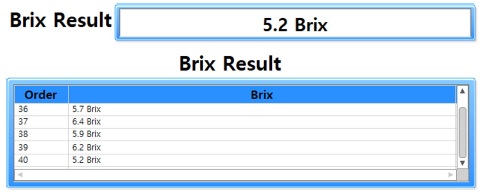
Fig. 9는 학습과 테스트 과정에서 사용되지 않은 새로운 방울토마토에 대한 당도 예측 결과를 보여준다. 좌측의 순번은 방울 토마토의 순서를 나타내며 우측의 Brix 값은 예측된 당도 수치를 나타낸다. Fig. 9에서는 현재 40번째 방울토마토까지 당도 예측이 진행되었고 해당 방울토마토의 당도 예측 값은 5.2 Brix임을 보여준다.
실험을 통하여 해당 과일의 평균 스펙트럼 데이터가 얻어지고 DNN(Deep Neural Network)에서 연산 처리된 후 당도 예측까지 걸리는 시간은 약 5초 이내였다. 이로부터 제안된 시스템의 실용화도 충분히 가능한 것으로 사료된다.
학습된 DNN(Deep Neural Network)에 대한 테스트 결과 당도 예측에서 80% 이상의 정확도를 보이고 있는 방울토마토의 개수는 280개로서 전체의 약 98%에 해당하는 높은 수치를 보이고 있다. 그러나 본 논문에서 사용된 굴절 당도계의 오차율이 0.1%인 점을 고려하면 당도 예측에서 더 높은 정확도가 요구된다. 앞으로 더욱 정확도를 높이기 위해서는 더욱 많은 학습 데이터가 준비되어야 할 것이다. 그리고 방울토마토를 회전시킬때 야기되는 광원과의 거리 변화에 따른 분광 스펙트럼의 오프셋 변동을 최소화하는 것이 필요할 것이다. 또한 장시간에 걸친학습 데이터 셋 준비 시에 주변 환경(주광, 형광등, 온도 등)의 변화를 충분히 차단하여야 하는 점도 고려되어야 한다.
5. 결 론
본 논문에서는 광대역 근적외선 광원을 이용하여 방울토마토의 투과 스펙트럼을 획득하고 이를 LabVIEW로 구현된 DNN(Deep Neural Network)의 입력 데이터로 사용하여 방울토마토의 당도를 예측하는 비파괴 지능형 시스템을 구현하였다. 그러나 동일한 과일임에도 불구하고 광의 입사 부위에 따라 투과 스펙트럼이 다를 수 있기 때문에 이를 해결하는 것이 필요하였다. 이를 위하여 분광기 앞에서 방울토마토를 1초 동안 회전시키면서 20개 부위에 해당하는 투과 스펙트럼을 얻고 이의 평균 스펙트럼을 구하여 DNN(Deep Neural Network)의 입력 데이터로 사용하였다. 또한 평균 스펙트럼을 구하는 과정에서 꼭지 부위에 해당하는 상이한 스펙트럼은 제거하였다.
평균 스펙트럼 데이터가 DNN(Deep Neural Network)에 입력된 후부터 당도를 예측하기까지 걸리는 시간은 약 5초 이내였다. 그리고 500개의 학습 데이터를 사용하여 학습된 DNN(Deep Neural Network)에 286개의 테스트 데이터를 적용한 결과 약98%의 방울토마토가 80~100%의 정확도를 보이고 있는 것으로 확인되었다. 이로부터 과일의 품질을 유지하면서 전문 인력 없이 당도를 측정할 수 있는 비파괴 지능형 당도 자동 측정 시스템의 실용화도 가능할 것으로 사료된다.
References
- https://www.nongmin.com/news/NEWS/POL/GOV/297778 /view?site_preference=normal (retrieved on Sep. 5, 2018).
- S. J. Choi, Introduction of Graphical Programming Lab-VIEW, dongil publisher, Seoul, pp. 14, 1998.
-
B. G. Lee, J. T. Lim, and J. S. You, “Utilization of Social Media Analysis using Big Data”, J. Korea Contents Assoc., Vol. 13, No. 2, pp. 211-219, 2013.
[https://doi.org/10.5392/JKCA.2013.13.02.211]

-
D. K. Choi and J. O. Park, “The Application Method of Machine Learning for Analyzing User Transaction Tendency in Big Data environments”, J. Korea Inst. Inf. Commun. Eng., Vol. 19, No. 10, pp. 2232-2240, 2015.
[https://doi.org/10.6109/jkiice.2015.19.10.2232]

- https://en.wikipedia.org/wiki/Machine_learning/(retrieved on Oct. 2018).
- https://terms.naver.com/entry.nhn?docId=830577&cid=423 44&categoryId=42344 (retrieved on Sep. 17, 2020).
- https://ko.dict.naver.com/#/entry/koko/c1cac885760f4530- ba1528eb2b4b1339 (retrieved on Sep. 17, 2020).
- https://terms.naver.com/entry.nhn?docId=5826803&cid=64 656&categoryId=64656 (retrieved on Sep. 17, 2020).