
IMU 기반 자세 추정 칼만필터에서 공분산 모델링이 추정 정확도에 미치는 영향
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A well-known difficulty in attitude estimation based on inertial measurement unit (IMU) signals is the occurrence of external acceleration under dynamic motion conditions, as the acceleration significantly degrades the estimation accuracy. Lee et al. (2012) designed a Kalman filter (KF) that could effectively deal with the acceleration issue. Ahmed and Tahir (2017) modified this method by adjusting the acceleration-related covariance matrix because they considered covariance modeling as a pivotal factor in the estimation accuracy. This study investigates the effects of covariance modeling on estimation accuracy in an IMU-based attitude estimation KF. The method proposed by Ahmed and Tahir can be divided into two: one uses the covariance including only diagonal components and the other uses the covariance including both diagonal and off-diagonal components. This paper compares these three methods with respect to the motion condition and the window size, which is required for the methods by Ahmed and Tahir. Experimental results showed that the method proposed by Lee et al. performed the best among the three methods under relatively slow motion conditions, whereas the modified method using the diagonal covariance with a high window size performed the best under relatively fast motion conditions.
Keywords:
Covariance, Attitude estimation, IMU, Kalman filter, External acceleration, Human motion tracking1. 서 론
제한된 공간에서 인체의 움직임을 측정하는 광학기반 모션캡처시스템과 달리, 관성 측정 장치(inertial measurement unit, 이하 IMU)는 공간의 제약을 받지 않는다는 특징을 지닌다. 따라서, 이동 중에 계측이 요구되는 인체 역학[1-5], 재활[6-8], 스포츠[9-11] 등 많은 분야에서 IMU의 적용이 각광을 받고 있다. 신체의 분절에 IMU를 부착하여 인체의 동작을 추정하는 관성 모션 캡처 시스템에 있어서, 신체 분절의 자세 추정은 인체의 움직임을 구성하기 위한 필수적인 절차이다.
칼만 필터(Kalman filter)는 IMU를 사용하여 자세를 추정하기 위해 가장 널리 사용되는 센서 신호 융합 알고리즘 중 하나이다. 지난 30년간 자세 추정을 위한 다양한 칼만 필터가 제안되었지만 근본적인 신호의 융합 방식은 동일하다[12-18]. 즉, 자이로스코프 신호를 적분하여 자세를 예측하지만, 예측된 자세값은 자이로스코프 신호에 섞여있는 잡음도 같이 적분되어 표류오차가 발생한다. 표류 오차를 억제하기 위해 가속도계 신호에 포함되는 중력 가속도를 이용하여 예측된 자세값을 보정하는 원리이다[12].
가속도계 신호와 관련하여 자세 추정 정확도를 저해시키는 주요 문제 중 하나는, 동적 조건에서 가속도계 신호는 중력 가속도뿐 아니라 외부 가속도를 포함하며 이 둘은 구분되지 않는다는 점이다[19]. 움직임이 빠른 경우, 가속도계 신호에서 중력가속도가 외부가속도에 비해 지배적이지 못하므로 가속도계 신호를 통한 보정 성능이 크게 저하된다.
가속도계 신호의 외부 가속도 문제를 효과적으로 처리하므로써 보다 높은 정확도의 자세를 추정하기 위해, 2012년 Lee 등[16]은 외부 가속도 보상 메커니즘을 갖는 칼만필터를 제안하였다. 여기서 외부 가속도는 마르코프 체인모델을 경유하여 칼만필터의 측정 공분산에 반영되므로써 보상되도록 설계되었다. 2017년 Ahmed and Tahir[17]는 앞서 언급된[16]의 방법에서 가속도 관련 측정 공분산을 변경하므로써 자세 추정 정확도를 향상시킬 수 있다고 발표하였다.
[16]의 방법과 [17]의 방법 간의 차이점은 가속도 관련 공분산의 모델링에 있다. [16]의 방법에서 가속도 공분산은 외부 가속도의 벡터 놈(norm)에 비례하되 외부 가속도의 방향별 크기에는 무관하게 분포하도록 모델링되었다. 반면 [17]의 방법에서는 외부 가속도의 방향별 크기에 따라 공분산의 해당 성분이 달라지도록 모델링되었다. 이 과정에서 공분산 행렬의 대각 성분만 취한 경우와 비대각성분까지 포함한 경우를 나누어 제안하였다. 또한, [16]의 방법에서 가속도 공분산은 직전 시간스텝(time step)의 외부가속도 정보만을 이용하여 도출하는 반면, [17]의 방법에서는 창 크기(window size)를 설정하여 다수개의 이전 시간스텝의 외부가속도들을 이용하여 계산하고 있다.
본 논문은 IMU기반 자세 추정 칼만필터에서 공분산 모델링이 추정 정확도에 미치는 영향을 고찰하고자 한다. 이를 위해,[16]의 방법과 [17]의 두가지 방법을 다양한 가속 조건 실험결과에서 비교분석하고자 한다. 특히, [17]의 방법의 차별적 특징이라고 할 수 있는 외부 가속도의 방향별 크기를 반영하는 공분산 모델링이 자세 추정 정확도 향상에 얼마나 기여를 하는지가 분석의 초점이라 할 수 있다.
2장에서는 동일한 칼만필터 구조 내에서 각 모델링의 차이점을 설명하고, 3장에서는 다양한 가속도 조건에서의 실험에 대해기술하고 있으며, 4장에서는 각 조건에서 방법별 추정 정확도 결과를 고찰한다.
2. 방 법
2.1 센서 모델링
참고문헌 [16]에서 가속도계 신호 yA와 자이로스코프 신호 yG는 다음과 같이 모델링 된다.
| (1) |
| (2) |
좌측 위첨자 S는 해당 벡터가 센서 좌표계에서 표시되었음을 의미한다. 위 식에서 sg는 센서의 중력 가속도, sa는 센서의 외부 가속도, 그리고 sω는 센서의 각속도이다. 또한, nG와 nA는 각각 자이로스코프와 가속도계의 신호 잡음이며, 이들은 서로 독립적이며 평균이 0인 화이트 가우시안 분포 잡음 (white Gaussian noise)이라 가정한다.
외부 가속도 sa는 다음과 같이 1차 프로세스로 모델링 된다.
| (3) |
여기서, ca는 0과 1사이의 모델 파라미터이며 εt는 시변(timevarying) 오차이다. 본 연구에서 ca는 비교 논문들과 같은 0.1로 설정하였다.
2.2 가속도 관련 공분산 모델링
본 논문의 목적은 앞서 소개한 참고문헌 [16]와 [17]이 제안하는 칼만 필터에 포함된 가속도 관련 공분산의 차이점이 자세 추정 정확도에 미치는 영향을 알아보기 위함이다. 가속도 관련 공분산에 대한 상세는 다음과 같다.
자세 벡터를 상태변수로 하는 자세 추정 칼만필터에 있어, 측정 모델은 다음과 같이 프로세스 모델로부터 예측된 가속도 의 오차항 을 사용 한다.
| (4) |
여기서, 우측 위첨자 −는 예측 (a priori)값을 의미하며 이후 식에 나오는 우측 위첨자 +는 수정 단계를 거친 보정 (a posteriori)값을 나타낸다.
가속도계 신호 모델과 외부 가속도 모델을 이용하여 위의 식(4)를 다음과 같이 표현할 수 있다.
| (5) |
여기서, 는 관성 좌표계의 Z축 단위벡터를 센서 좌표계에서 관측한 자세 벡터로서 관성 좌표계 {I}에서 바라본 센서 좌표계 {S}의 자세행렬 의 마지막 행벡터의 전치벡터로 롤과 피치 정보를 포함하고 있다.
위의 측정 모델을 통해 측정 모델의 화이트 가우시안 측정 잡음 성분 vt와 공분산 행렬 Mt은 다음과 같이 표현된다.
| (6) |
| (7) |
여기서 와 nA는 서로 독립적이므로 Mt 항은 ΣA와 Σacc항으로 나누어 표현할 수 있다. 첫째, ΣA는 가속도계 신호 잡음 성분 nA의 공분산 행렬이며 로 나타내고 그 값은 정의된다. 여기서 가속도계 신호 잡음 분산이 각 축에 대해 같다고 가정하였을 때 얻을 수 있다. 두번째로, Σacc은 가속도 모델 오차항의 공분산 행렬 로 표현된다. 본 논문에서는 이 행렬을 가속도 관련 공분산이라 칭하며, 가속도 관련 공분산은 본 논문의 주된 연구대상이다.
Σacc는 시변항이며 분석적으로 얻을 수 없기 때문에 Σacc의 값을 선정해야 한다. [16]에서는 와 가 관련되어 있지 않다고 가정하였으므로 이 적용되었다. 또한, 일반적으로 외부 가속도의 기대값은 0으로 가정되므로, 이 적용되었다. 따라서 Σacc는 다음과 같이 정의된다.
| (8) |
참고문헌 [16]에서는 아래 식과 같이, 식 (8)의 Σacc을 각 성분이 벡터 의 크기(norm)를 고르게 나누어 갖는 대각 행렬로 모델링하였다
| (9) |
식 (9)에서 보여지듯, 참고문헌 [16]에서는 가속도 관련 공분산이 외부 가속도의 방향별 크기에 무관하게 3축 모두에 동일하게 설정되고 있다.
참고문헌 [17]에서는 이 점에 주목하였다. 임의의 외부 가속도는 특정 축에 집중되어 발생될 수 있으며, 이러한 경우 [16]와 같은 설정은 추정 정확도의 저하를 유발할 수 있다고 주장하였다. 이를 보완하고자, [17]에서는 각 축이 외부 가속도의 크기에 따라 다른 가중치의 공분산 값을 갖도록 다음과 같이 제안하였다.
| (10) |
여기서, M1은 공분산을 대체하는 이동 평균 계산에 사용되는 창 크기 (window size)이다. M1이 클수록 긴 시간 동안의 속도 평균을 사용할 수 있지만, 계산량이 많아지므로 칼만필터의 연산 효율에 저하가 발생한다. 반면, M1이 작을수록 필터의 효율을 보장할 수 있지만 변동성을 갖는 조건에서는 좋은 자세 추정 성능을 보장할 수 없다 [17]. 제안된 Σacc은 특정 축의 가속도 값이 증가함에 따라 그 축에 연관된 공분산 행렬의 성분이 비례적으로 증가하게 된다. 이로 인해 칼만 이득 (Kalman gain)을 축 방향별로 상이하게 다룰 수 있다.
식 (10)의 Σacc은 각 축의 외부 가속도 성분이 서로 연관되어 있지 않다는 가정하에 대각 행렬로 구성되었다. 하지만 각 축성분이 서로 연관되어 있다고 가정할 경우 Σacc은 대각 성분과 비대각 성분을 모두 포함하도록 다음과 같이 변경된다.
| (11) |
본 논문은 앞서 소개한 세 가지의 가속도 측정 공분산, 식(9)~ (11)로 칼만필터를 구성하여, 가속도 관련 공분산이 자세 추정 정확도에 미치는 영향을 고찰하고자 한다.
2.2 가속도 관련 공분산 모델링
선형 칼만필터는 다음과 같이 각각 진행 모델과 측정 모델로 구성된다.
| (12) |
| (13) |
여기서 xt는 상태 벡터, Φt−1는 상태 전이행렬, zt는 측정 벡터, 그리고 H는 관측행렬이다. 또한, wt−1와 vt는 각각 진행 모델과 측정 모델의 백색 가우시안 잡음 성분들이며, 각각 공분산 행렬 Qt−1와 Mt을 갖는다. 본 논문에서 다루는 칼만필터에서 상태 벡터 xt는 롤과 피치 정보를 포함하고 있는 SZt로 설정되며, H는 식 (5)에 따라 gI3로 표현된다.
각각의 가속도 관련 공분산에서 스트랩다운 적분 차수가 자세 추정 정확도에 미치는 영향을 알아보기 위해, SZt는 참고문헌 [18]에서 소개된 1차와 2차 스트랩다운 적분을 사용하여 다음과 같이 구성한다.
| (14-1) |
| (14-2) |
여기서 At-1는 에 해당하며, Δt는 샘플링 시간, 그리고 는 각속도 벡터 Sω의 외적을 나타내는 의대칭(skewsymmetric) 행렬이다. 위 식에 센서 모델링 식 (2)을 대입하여 정리하면, 1차와 2차 적분식에 해당하는 Φt−1는 각각 다음과 같이 정리할 수 있다.
| (15-1) |
| (15-2) |
마찬가지 방법으로 1차와 2차 적분식에 해당하는 wt−1는 다음과 같다.
| (16-1) |
| (16-2) |
식 (13)에서 측정 모델 잡음 vt에 해당하는 공분산 행렬 Mt은 2.2절에서 설명한 세 가지의 경우로 나누어 분석을 진행한다. 칼만 필터를 구성하는 상세 내용은 [16]을 참조한다.
3. 실 험
비교 논문에서 제안된 세 가지 가속도 관련 공분산에 따른 자세 추정 정확도를 분석하기 위한 실험을 실시하였다. 실험을 위해 3축 가속도계와 3축 자이로스코프를 포함하는 IMU인 MTw(Xsens Technologies B. V., Netherlands)를 사용하였다. 실험을 통해 얻은 추정값의 정확도를 비교하기 위하여 자세 참조값은 광학식 모션 캡처 시스템인 Opitrack Flex13 (Natural Point, USA)을 사용하여 얻었다.
세 가지 서로 다른 가속도 관련 공분산을 사용한 방법들 간의 자세 추정 정확도를 비교하였다. 여기서, 식 (9), (10), 그리고 (11)을 사용한 방법을 각각 Method 1, Method 2, 그리고 Method 3라 칭한다. 추정 정확도 비교를 위해 롤과 피치의 RMSE (root mean squared error) 평균이 사용되었다.
실험은 손으로 MTw를 잡고 임의로 자세를 변화시키며 진행되었으며, 동시에 MTw에 부착된 Flex13의 마커들을 통해 자세행렬 참조값 이 구해졌다 (Fig. 1 참조). MTw 와 Flex13 모두 100 Hz로 샘플링하여 데이터를 추출하였다. 가속 조건에 따라 3가지의 경우(Cases 1~3)로 나누었으며, 각 경우 별로 3번의 실험이 진행되었다. Case 1, 2, 그리고 3의 평균 가속도는 각각 0.45 m/s2, 1.93 m/s2, 그리고 4.08 m/s2이었으며, 평균 실험 시간은 각각 40초, 2분, 그리고 2분이었다.
가속도 관련 공분산이 자세 추정 정확도에 미치는 영향을 다양한 조건에서 확인하기 위하여, 세 가지 인자를 고려하였다: (i)가속도 조건, (ii) 스트랩다운 적분 차수, 그리고 (iii) (Method 2와 3에 한하여) 창크기 M1.
4. 결과 및 고찰
Table 1은 세 가지 가속 조건과 두 가지 스트랩다운 적분 차수별로 각 방법들의 추정 RMSE를 보여준다. 여기서 RMSE는 각 경우별로 3번씩 진행한 실험에 대한 롤과 피치의 평균 RMSE이며, Method 2와 3의 경우 M1은 15를 기준으로 하였다.
첫째, 스트랩다운 적분 차수로 인한 각 방법들의 RMSE 변화량을 살펴본다. 저속 조건인 Case 1은 RMSE의 변화량이 0으로, 적분 차수에 따른 자세 추정 정확도의 개선을 보여주지 못하였다. Case 2와 Case 3에서는 각각 평균 0.29°와 1.20°의 RMSE개선 효과를 보였다. Case 2와 Case 3의 평균 자이로스코프 각 속도는 2.7 rad/s로 같지만 RMSE 개선량의 차이가 나는 것으로 보아 평균 가속도가 높아짐에 따라 적분 차수에 따른 RMSE의 개선량이 높아짐을 알 수 있었다. 또한 Method 1, Method 2 그리고 Method 3 순으로 RMSE의 개선효과 좋아졌다. 하지만 Method 3는 가장 좋은 RMSE 개선 효과에도 불구하고 대부분의 결과에서 세가지 방법 중 가장 좋지 않은 성능을 보였다. 둘째, 적분 차수를 기준으로 가속도 조건별 각 방법들의 RMSE를 비교한다. 1차 스트랩다운 적분 차수일 때, Case 1의 외부 가속도 크기는 0.45 m/s2으로 매우 작기 때문에 세 방법 모두 좋은 추정 성능을 보였다. Case 2의 경우 Method 2의 성능이 가장 좋았으며, Case 3에서는 Method 1의 추정 성능이 가장 좋았다. 2차 스트랩다운 적분일 때, Case 1에서는 1차 적분 차수일 때와 같이 세 방법 모 두 성능의 차이를 보이지 않았다. Case 2와 Case 3에서는 각각Method 2, Method 1의 추정 성능이 가장 좋았다. Method 3는 1차와 2차 모든 적분 차수에서, 가속도가 증가할수록 다른 두 방법들보다 현저하게 추정 성능이 저하되었다.
Fig. 2은 각 가속도 조건 (3 가지)별로 진행한 3번의 실험에서 (총 9회), 각 가속도 조건 중 하나의 대표적인 실험을 선정하여 M1의 크기에 따른 자세 추정 RMSE를 보여준다. 따라서, 모든 실험 결과의 평균을 사용한 Table 1과 결과가 상이할 수 있다. Method 1의 가속도 관련 공분산은 M1와 상관없기 때문에 동일한 RMSE를 갖는다. Method 2와 Method 3는 세 가지의 가속도 조건에서 모두 M1의 크기에 따라 비슷한 경향을 보인다. 첫째, 저속 조건인 Case 1 에서, Method 1이 세 방법 중 가장 좋은 자세 추정 성능을 보여줬다. Method 2와 Method 3는 M1이 높아짐에 따라 초반에는 RMSE가 증가하는 경향을 보였고 그 이후부터는 M1에 따른 어떤 경향성을 띄지 않았다. 둘째, Case 2에서 Method 2와 Method 3는 M1이 10~20까지 증가할 때 확실한 RMSE의 감소를 보였으며 Method 2가 가장 좋은 성능을 보여주었다. 그 이후부터는 M1의 증가에 따른 성능의 뚜렷한 변화가 보이지 않았다. 셋째, 가장 높은 평균 가속도를 갖는Case 3에서는 M1을 100까지 증가시킬 때까지 Method 2와 Method 3는 꾸준한 RMSE의 감소를 보였다. M1의 크기가 작을 때에는 Method 1의 성능이 가장 좋았지만, M1의 크기가 45보다 커질 때부터 Method 2의 성능이 가장 좋았다. 반면, Method 3는 대부분의 구간에서 가장 좋지 않은 성능을 보이었다.
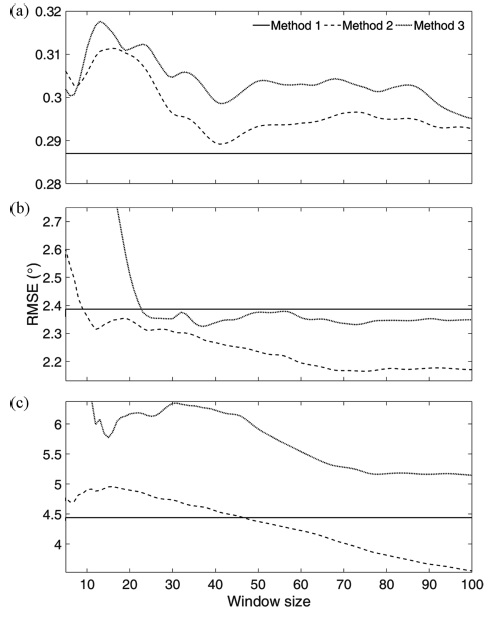
Sample of RMSE results (unit: °) of attitude estimation with respect to the window size from (a) Case 1, (b) Case 2, and (c) Case 3.
가속도가 낮은 Case 1에서는 M1의 변화가 자세 추정 성능에 큰 영향을 끼치지 않았지만, 가속도가 높아질수록 M1의 변화에따른 추정 성능의 변화가 컸으며, 대체로 M1이 증가함에 따라 추정 성능이 향상되는 경향을 보였다. 외부 가속도와 M1의 크기가 증가할수록, Method 2 가 현저한 성능의 향상을 보이며 세 방법 중 가장 좋은 정확도를 보였다.
Fig. 3는 M1=15일 때 추정 오차에 대한 예로서, 일정 시간 (10초~20초) 동안의 오차 결과를 보여준다. 세 방법 모두 같은 구조의 칼만필터에서 가속도 관련 공분산만 다르게 설정하였기 때문에 비슷한 형상의 오차 그래프를 보여주었다.
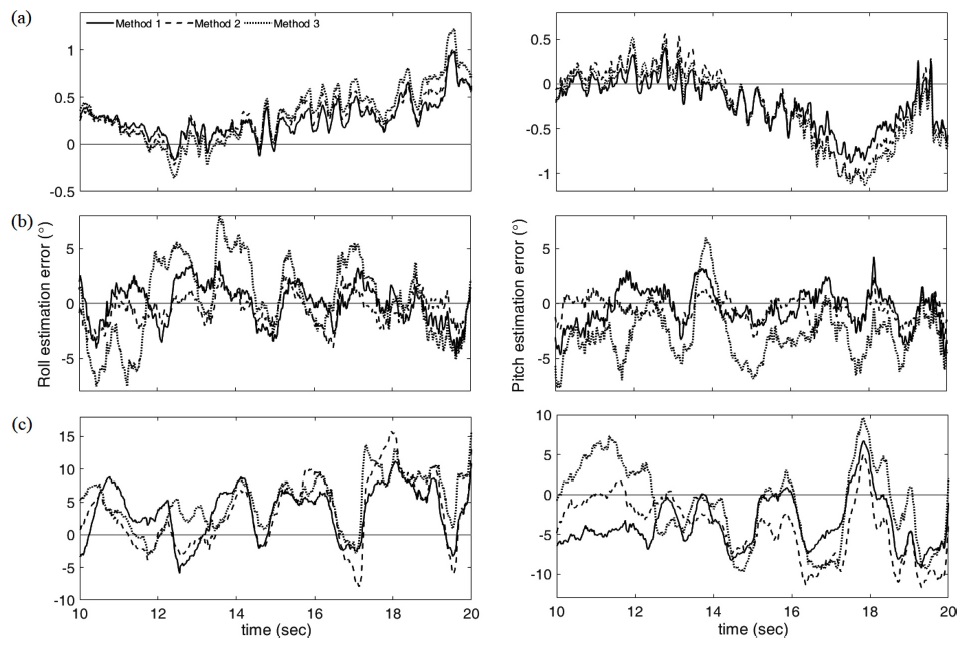
Samples of the roll (left) and pitch (right) estimation errors when M1 = 5 : (a) Case1, (b) Case2 and (c) Case 3.
Method 2와 Method 3 모두 특정 축의 가속도 값이 증가함에 따라 그 축에 연관된 공분산 행렬의 성분이 비례적으로 증가한다는 개념으로 가속도 관련 공분산을 다룬다. 하지만 각 축의 가속도 성분이 연관되어 있다고 가정하여, 비대각 성분이 포함된 공분산 행렬을 사용하는 Method 3는 대부분의 실험에서 가장 좋지 않은 결과를 보여주었다. 즉, 본 연구의 결과에 있어서는, 가속도 관련 공분산 행렬에 포함된 비대각 성분들은 칼만필터의 자세 추정 성능을 저하시켰다.
5. 결 론
본 논문은 참고문헌 [16]와 [17]에서 제안한 칼만 필터를 비교함으로 가속도 관련 공분산의 모델링 차이가 IMU 기반 자세 추정 정확도에 미치는 영향을 분석하였다.
[16]에서 제안한 가속도 모델 보상 메커니즘을 기반으로 한 선형 칼만 필터는 대각 성분만을 포함하는 가속도 관련 공분산 행렬을 사용하며 공분산의 각 성분은 같은 값을 갖는다. 하지만 [17]은 [16]에서 제안한 방법을 수정하여 가속도 관련 공분산을 조정하여 외부 가속도의 각 축에 따라 공분산 행렬의 성분이 다른 값을 갖도록 모델링하였다. [17]이 제안한 두 가지의 방법 중 하나는 대각 성분만을 포함한 공분산 행렬을 사용하고, 다른 하나는 비대각 성분과 대각 성분을 모두 포함한 공분산을 사용한다. 또한 [17]의 두 방법은 창크기 M1에 따라 자세 추정 성능이변동된다.
세 방법 (즉, [16] 제안 방법과 [17] 제안 방법 두가지)에 대한 비교결과, 상대적으로 느린 동적 조건에서는 [16]에서 제안한 Method 1이 세가지 방법 중 가장 좋은 결과를 보였다. 가속도와 평균 연산자의 크기가 증가함에 따라, [17]에서 제안한 방법 중 대각 공분산 행렬을 사용하는 Method 2가 가장 좋은 결과를 보였다. 반면에 [17]에서 제안한 방법 중 비대각 성분과 대각 성분을 모두 포함한 공분산을 사용하는 방법인 Method 3은 대부분의 실험에서 가장 좋지 않은 결과를 보였다.
적분 차수에 따른 추정 성능 개선 효과에 대해서는, 세가지 방법 모두 가속도가 올라감에 따라 추정 정확도 향상이 확인되었으며, 특히 Method 3에서 개선 효과가 두드러졌다.
결론적으로, 가속도 관련 공분산을 모델링함에 있어, 가속도의 방향별 크기의 차이를 반영하는 공분산 모델링은 제한적으로 효과가 있음을 확인하였다. 또한, 가속도 관련 공분산에서 비대각 요소는 성능에 좋지 않은 영향을 미치는 것을 확인하였다. Method 2는 적절한 창 크기 M1을 선정해야 한다는 점에서 불편함이 있으나, 매우 빠른 운동 조건에서는 Method 1 보다 정확한 추정을 기대할 수 있다는 점에서 고려할 만하다. 따라서, IMU기반 자세 추정시, 운동 조건 등을 고려한 최적의 칼만필터를 선정할 필요가 있다.
Acknowledgments
본 연구는 2018년도 정부(교육부)의 재원으로 한국연구재단 기초연구사업 (No. 2018R1D1A1B07042791)의 지원을 받아 수행됨.
References
-
H. Zhou, H. Hu, and Y. Tao, “Inertial measurements of upper limb motion”, Med. Biol. Eng. Comput., Vol. 44, No. 6, pp. 479-487, 2006.
[https://doi.org/10.1007/s11517-006-0063-z]

-
H. Zhou, T. Stone, H. Hu, and N. Harris, “Use of multiple wearable inertial sensors in upper limb motion tracking”, Med. Eng. Phys., Vol 30, No. 1, pp. 123-133, 2008.
[https://doi.org/10.1016/j.medengphy.2006.11.010]

- W. C. Jung and J. K. Lee, “Comparison of drift reduction methods for pedestrian dead reckoning based on a shoemounted IMU”, J. Sens. Sci. Technol., Vol. 28, No. 6, pp. 345-354, 2019.
-
A. Atrsaei, H. Salarieh, A. Alasty, and M. Abediny, “Human arm motion tracking by inertial/magnetic sensors using unscented Kalman filter and relative motion constraint”, J. Intell. Robot. Syst., Vol. 90, No. 1-2, pp. 161–170, 2018.
[https://doi.org/10.1007/s10846-017-0645-z]

-
B. Fasel, J. Spörri, J. Chardonnens, J. Kröll, E. Müller, and K. Aminian, “Joint inertial sensor orientation drift reduction for highly dynamic movements”, IEEE J. Biomed. Health Inform., Vol. 22, No. 1, pp. 77-86, 2018.
[https://doi.org/10.1109/JBHI.2017.2659758]

-
Y. L. Hsu, P. C. Chung, W.H. Wang, M. C. Pai, C. Y. Wang, C. W. Lin, H. L. Wu, and J. S. Wang, “Gait and balance analysis for patients with Alzheimer's disease using an inertial-sensor-based wearable instrument”, IEEE J. Biomed. Health Inform., Vol. 18, No. 6, pp. 1822-1830, 2014.
[https://doi.org/10.1109/JBHI.2014.2325413]

-
J. K. Lee, “Determination of fall direction before impact using support vector machine”, J. Sens. Sci. Technol., Vol. 24, No. 1, pp. 47-53, 2015.
[https://doi.org/10.5369/JSST.2015.24.1.47]

-
G. Cooper, I. Sheret, L. McMillian, K. Siliverdis, N. Sha, D. Hodgins, L. Kenney, and D. Howard, “Inertial sensor-based knee flexion/extension angle estimation”, J. Biomech., Vol. 42, No. 16, pp. 2678-2685, 2009.
[https://doi.org/10.1016/j.jbiomech.2009.08.004]

-
J. B. Lee, R. B. Mellifont, and B. J. Burkett, “The use of a single inertial sensor to identify stride, step, and stance durations of running gait”, J. Sci. Med. Sport, Vol. 13, No. 2, pp. 270-273, 2010.
[https://doi.org/10.1016/j.jsams.2009.01.005]

-
C. N. K. Nam, H. J. Kang, and Y. S. Suh, “Golf swing motion tracking using inertial sensors and a stereo camera”, IEEE Trans. Instrum. Meas., Vol. 63, No. 4, pp. 943-952, 2013.
[https://doi.org/10.1109/TIM.2013.2283548]

-
M. Supej, “3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system”, J. Sports Sci., Vol. 28, No. 7, pp. 759-769, 2010.
[https://doi.org/10.1080/02640411003716934]

-
A. M. Sabatini, “Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing”, IEEE Trans. Biomed. Eng., Vol. 53, No. 7, pp. 1346-1356, 2006.
[https://doi.org/10.1109/TBME.2006.875664]

-
G. Ligorio and A. M. Sabatini, “A novel Kalman filter for human motion tracking with an inertial-based dynamic inclinometer”, IEEE Trans. Biomed. Eng., Vol. 62, No. 8, pp. 2033-2043, 2015.
[https://doi.org/10.1109/TBME.2015.2411431]

-
D. S. Yun and H. S. Yu, “Extended Kalman filter design for autonomous navigation with GPS and INS sensor system fusion”, J. Sens. Sci. Technol., Vol. 16, No. 4, pp. 294-300, 2007.
[https://doi.org/10.5369/JSST.2007.16.4.294]

-
J. K. Lee and M. J. Choi, “Robust inertial measurement unit-based attitude determination Kalman filter for kinematically constrained links”, Sensors, Vol. 19, No. 4, pp. 768, 2019.
[https://doi.org/10.3390/s19040768]

-
J. K. Lee, E. J. Park, and S. N. Robinovitch, “Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions”, IEEE Trans. Instrum. Meas., Vol. 61, No. 8, pp. 2262-2273, 2012.
[https://doi.org/10.1109/TIM.2012.2187245]

-
H. Ahmed and M. Tahir, “Improving the accuracy of human body orientation estimation with wearable IMU sensors”, IEEE Trans. Instrum. Meas., Vol. 66, No. 3, pp. 535-542, 2017.
[https://doi.org/10.1109/TIM.2016.2642658]

-
J. K. Lee and M. J. Choi, “Effect of strapdown integration order and sampling rate on IMU-based attitude estimation accuracy”, Sensors, Vol. 18, No. 9, pp. 2775, 2018.
[https://doi.org/10.3390/s18092775]

-
J. K. Lee, “Kalman filter for estimation of sensor acceleration using six-axis inertial sensor”, Trans. Korean Soc. Mech. Eng. A, Vol. 39, No. 2, pp. 179-185, 2015.
[https://doi.org/10.3795/KSME-A.2015.39.2.179]


