[ Article ]

JOURNAL OF SENSOR SCIENCE AND TECHNOLOGY - Vol. 34, No. 2, pp.130-137

ISSN: 1225-5475 (Print) 2093-7563 (Online)

Print publication date 31 Mar 2025

Received 06 Mar 2025 Revised 07 Mar 2025 Accepted 11 Mar 2025

DOI: https://doi.org/10.46670/JSST.2025.34.2.130

Comparative Study on the Robustness against Gyroscope Bias of Rule-based and Machine-Learning-based Attitude Estimation Approaches

Ji Hoon Park¹

; Chang June Lee²

; Jung Keun Lee¹^{, +}

1School of ICT, Robotics and Mechanical Engineering, Hankyong National University, 327 Jungang–ro, Anseong, Gyeonggi 456-749, Korea
2Department of Integrated Systems Engineering, Hankyong National University, 327 Jungang–ro, Anseong, Gyeonggi 456-749, Korea

Correspondence to: ⁺ jklee@hknu.ac.kr

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Attitude estimation based on a six-axis inertial measurement unit (IMU) consisting of an accelerometer and a gyroscope is a fundamental technology utilized in various applications. Accordingly, IMU-based attitude estimation methods have been widely studied using rule-based algorithms and machine learning (ML) techniques. Among the factors contributing to estimation errors, the bias inherent in the gyroscope signals is particularly significant. Although numerous studies have focused on bias compensation methods, studies on the robustness of attitude estimation methods against gyroscope biases of various magnitudes are scarce. Therefore, this study aimed to compare and analyze the robustness of rule-based and ML-based attitude estimation methods against different magnitudes of gyroscopic bias. In this study, higher robustness was defined as lower performance degradation. The bias compensation mechanism exhibited outstanding performance in compensating for constant biases, leading to a substantial difference in the estimation performance of rule-based algorithms depending on the presence of bias compensation. In addition, bias augmentation did not enhance the robustness of ML-based methods. Finally, rule-based algorithms incorporating bias compensation mechanisms exhibited superior robustness against biases compared with ML-based methods.

Keywords:

Attitude estimation, Gyroscope bias, Rule-based algorithm, Machine learning, Robustness

1. INTRODUCTION

Accurate attitude estimation is crucial for a wide range of autonomous systems, including unmanned aerial vehicles, robots, and handheld devices [1-9]. In these systems, inertial measurement units (IMUs), specifically gyroscopes, play a fundamental role in measuring angular rates, which are then integrated to estimate the orientation over time. Despite their importance, gyroscopes are subject to various sources of error, among which gyroscopic bias is one of the most significant. The gyroscope bias refers to a nonzero sensor output when there is no actual rotation, leading to a cumulative drift in the estimated orientation.

Traditionally, rule-based methods, such as the Kalman filter (KF) or complementary filter (CF), have been widely adopted to fuse IMU data for attitude estimation [3-7,9-14]. Rulebased algorithms process data based on explicitly defined mathematical models and logic. These algorithms estimate attitudes using sensor data and system dynamics based on predefined rules. In the context of attitude estimation, rulebased approaches generally interpret IMU data using physical models and signal processing techniques. Rule-based algorithms often apply bias compensation mechanisms to address the errors caused by gyroscopic bias.

However, in recent years, machine learning (ML) approaches have attracted attention as alternative or complementary methods for attitude estimation [15-21]. These methods often leverage large datasets to learn complex sensor-to-attitude mappings, potentially capturing nonlinearities and sensor-specific nuances more effectively than the traditional filtering approaches. An ML-based method can apply bias augmentation during the training process to mitigate the effects of gyroscopic bias.

Despite the widespread popularity of rule-based approaches and the considerable potential of ML-based approaches, comparative studies focusing on the robustness of these methods to gyroscopic bias are scarce. Although numerous studies have demonstrated how rule-based and ML-based approaches perform under typical conditions, few studies have investigated the reliability of each method when the gyroscope bias is systematically varied or under real-world conditions where the sensor offset can be significant. Understanding this robustness is vital because an unaccounted bias can lead to substantial orientation errors when integrated over time, which may compromise navigation, control, and safety in autonomous operations.

This study compared and analyzed the robustness of rulebased and ML-based methods against gyroscopic bias, where robustness was evaluated by comparing the performance at different bias levels. In this context, a greater performance degradation owing to gyroscope bias indicates lower robustness. The objective of this study was to assess which attitude estimation method is more robust to bias based on the analysis results.

The remainder of this paper is organized as follows: Section 2 introduces the estimation methods of both rule-based and ML-based approaches along with a review of related studies. Section 3 presents the validation methodology for robustness, the types of validation data, and the process of generating validation bias. In Section 4, the performance of each method in attitude estimation using validation data is analyzed, and the performance and robustness of the rulebased and ML-based methods are compared. Additionally, the results are discussed, highlighting the key insights into the robustness of each method against gyroscopic bias. Finally, Section 5 presents the conclusions and outlines possible directions for future studies.

2. LITERATURE REVIEW

2.1 Rule-based Method

The rule-based method is based on the strapdown integration of the gyroscope signal and the vertical reference vector of the accelerometer. First, the gyroscope signal is modeled as follows:

y G = S ω + b G + n G

(1)

Here, ^Sω is the actual angular velocity, b_G is the bias, n_G is the noise, and the left superscript S indicates that the vector was observed at the sensor coordinate system {S}. Using the gyroscope signal, the sensor orientation of the sensor coordinate system {S} with respect to the inertial coordinate system {I} at discrete time t was computed through strapdown integration as follows:

S I R t = S I R t - 1 e x p ⁡ S y G, t - 1 × Δ t

(2)

where Δt is the sampling time, and [^Sy_G,t−1×] is the cross-product matrix of ^Sy_G,t−1, which is represented as follows:

s y G, t - 1 × = 0 - y G, z y G, y y G, z 0 - y G, x - y G, y y G, x 0

(3)

However, strapdown integration has a drift error problem owing to the accumulation of sensor errors during integration, and several studies have employed rule-based sensor fusion algorithms [4,5,7,10-14], such as the KF and CF, which fuse the gyroscope and accelerometer signals to compensate for the drift error. These rule-based algorithms determine the optimal attitude by determining the fusion weights based on sensor noise covariance or model parameters. As these algorithms update the state information recursively, they are effective for real-time attitude estimation.

Lee et al. [10] proposed a KF to estimate the vertical reference vector, where the external acceleration was modeled as a Markov chain process. However, this method does not incorporate a gyroscopic bias compensation mechanism. Roetenberg et al. [11] proposed an error-state KF to estimate and compensate for various factors. The KF determines and compensates for the orientation error, gyroscope bias, and disturbance. Laidig et al. [12] proposed an algorithm for attitude quaternion estimation and employed a KF to estimate and compensate for gyroscope bias in both static and dynamic states.

2.2 ML-based Method

ML-based methods employ ML models, such as recurrent neural networks (RNNs), for attitude estimation. An RNN is an ML model suitable for time-series processing, and long short-term memory and gated recurrent units (GRU) are derived from the basic RNN to solve the long-term dependency problem. Recent studies have combined ML- and rule-based filter algorithms or developed end-to-end RNNtype models to estimate attitudes based on IMU signals [15,16,18,21]. This study focused on an end-to-end RNN model for attitude estimation.

Weber et al. [15] proposed an end-to-end GRU model developed to solve the long-term dependency problem for estimating attitude quaternions using accelerometer signals, gyroscope signals, and sampling time as model inputs. Choi et al. [16] developed a parallel model consisting of two separate GRU models for estimating the attitude and heading. The former model receives accelerometer and gyroscope signals and outputs a vertical reference vector. These studies applied data augmentation to datasets of various dynamic scenarios and used them for model training to improve the learning performance of the model [15,16,22-29]. In both studies, data augmentation was implemented by adding a sensor bias or noise to the signal of the original dataset or by applying rotation. Furthermore, a follow-up study of [16] investigated the effects of data augmentation on the attitude estimation performance [22].

3. METHODOLOGY

This study aimed to compare the robustness of rule-based and ML-based methods against gyroscopic bias. In this study, three methods (M1–M3) were selected as rule-based methods and three methods (M4–M6) were selected as ML-based methods.

For rule-based methods, M1 is the KF proposed in [10] for estimating the vertical reference vector and M2 is an error-state KF available in MATLAB, which is an extension of the KF proposed in [12]. M3 is the quaternion-estimation algorithm proposed in [12]. Among these, M1 was selected as the method without bias compensation, whereas M2 and M3 were selected as the methods incorporating a bias compensation mechanism.

Among the ML methods, M4 and M5 are the GRU models proposed in [16] for estimating the vertical reference vector, and M6 is the GRU model proposed in [15] for quaternion estimation. To investigate the effect of bias augmentation on the robustness against gyroscopic bias, we compared models without bias augmentation (M4) and with bias augmentation (M5 and M6). To compare the robustness against gyroscope bias owing to data augmentation, bias augmentation was not applied to M4 (which had the same model structure and training data size as M5), whereas it was applied to M5 and M6.

The evaluation dataset was obtained from a validation dataset used in [16]. The dataset consists of 9-axis IMU signals from the MTw (Xsens Technologies B.V., Enschede, The Netherlands) and the truth reference of the attitude measured using an optical motion capture system, OptiTrack Flex 13 (NaturalPoint, Inc., Corvallis, OR, USA). The data from both systems were recorded at a sampling rate of 100 Hz. All the experimental data included a rest period of approximately 20 s at the beginning and end of the experiment. Furthermore, as this study required validation data containing static states for accurate gyroscope bias estimation and removal, only 112 datasets obtained by attaching the IMU to a rigid body rather than a human body segment were used for validation.

In this study, to assume situations where it is easy and difficult to remove bias, the performance was compared for the following two cases: Case 1, where static intervals were included, and Case 2, where static intervals were removed. Cases 1 and 2 enable a comparison of the bias compensation effects depending on the presence or absence of static intervals.

The performance of the selected comparison group was analyzed according to different validation bias magnitudes to evaluate robustness. The original bias in the dataset must be removed to ensure accurate evaluation under predefined bias magnitudes. Thus, we eliminated bias using the gyroscope signals during the rest intervals of each dataset and then applied predefined validation bias vectors to the gyroscope signals for validation. As bias can occur in different directions for each of the three axes, validation bias vectors were generated and applied using the following procedure: (i) A random seed was set for each bias magnitude to generate bias vectors with random directions. (ii) The random function in MATLAB was used to generate normally distributed random numbers, creating 112 three-dimensional vectors corresponding to the number of validation dataset samples. Each vector was normalized to obtain a unit vector in a random direction. (iii) The predefined bias magnitudes were multiplied by the unit vectors to generate 112 validation bias vectors with fixed magnitudes and random directions. The generated constant-bias vectors were applied to the corresponding validation datasets.

The validation biases were set to realistic magnitudes. Measurements of MEMS-based IMU biases in our laboratory indicated that the bias magnitudes were within 2.5°/s. Therefore, this value was chosen as the maximum realistic bias magnitude. To examine the performance variations at different bias levels, the validation bias magnitudes were set to 0, 0.5, 1, 1.5, 2, and 2.5°/s.

4. RESULTS AND DISCUSSIONS

4.1 Results

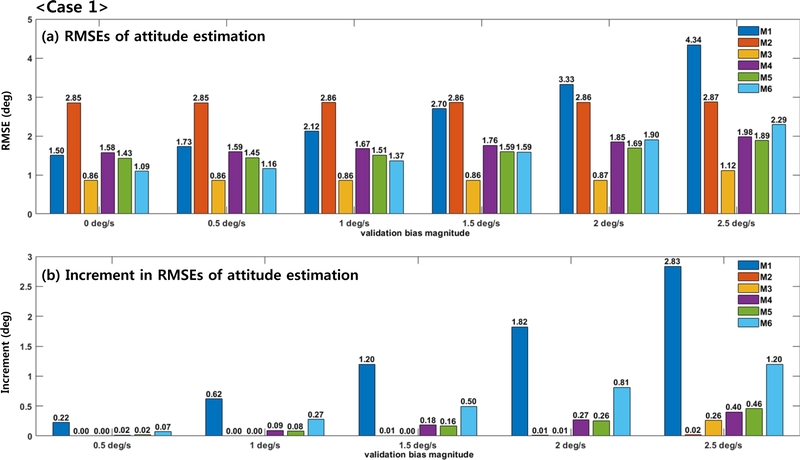
Robustness against bias can be evaluated based on the degradation in the estimation performance owing to bias. Therefore, in this study, as an evaluation metric, the robustness to validation gyroscope bias was evaluated using the increment of the root mean square errors (RMSEs) of the roll and pitch angles. The RMSE increment was derived by comparing it with the baseline condition in which the bias was 0°/s (i.e., the bias-free condition). Fig. 1 shows the attitude RMSE and its increment for the six comparison methods in Case 1, including static intervals. As shown in Fig. 1, M3 and M6 exhibited superior estimation performances in the baseline condition, with the RMSEs of 0.86° and 1.09°, respectively, whereas M2 showed the worst estimation performance with an RMSE of 2.85°. The remaining methods (M1, M4, and M5) exhibited moderate performances, with RMSEs ranging from 1.43° to 1.58°. In terms of the RMSE increment, the RMSE of M1 increased by 2.83° as the bias increased from 0 to 2.5°/s, which was the largest among the six methods. M6 showed an RMSE increment of 1.20° as the bias increased by 2.5°/s, whereas M2–M5 showed an RMSE increment of less than 0.5° as the bias increased. The RMSE increment of M2 was 0.02°, which was highly insignificant, whereas that of M3 remained at 0.01° until the bias reached 2°/s, but sharply increased to 0.26° at 2.5°/s.

Fig. 1.

(a) RMSE and (b) increment in RMSE compared with when the bias was 0°/s for Case 1 (unit: °)

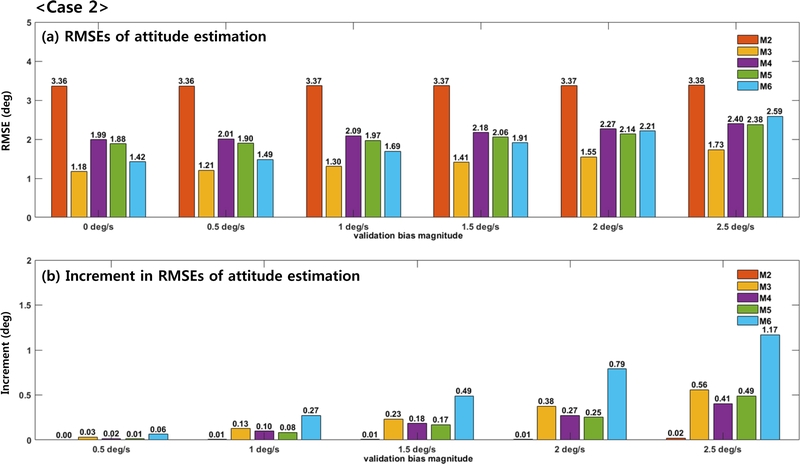
Fig. 2 shows the attitude RMSE and its increase in Case 2 after removing the static intervals. In this case, M1 cannot obtain an accurate initial reference vector, which leads to an inaccurate attitude estimation. Accordingly, M1 was excluded from the results of Case 2 because it was difficult to analyze the robustness of the bias owing to the significant errors caused by the absence of the initial static intervals. Fig. 2 indicates that all the methods exhibited a higher RMSE in Case 2 than in Case 1 because static intervals were not included. Similar to Case 1, M3 showed the best performance with an RMSE of 1.18°, whereas M2 showed the worst performance with an RMSE of 3.36°. In the baseline, M6 (1.42°), M5 (1.88°), and M4 (1.99°) showed superior performances in that order, but as the bias increased to 2.5°/s, the error of M6 (2.59°) exceeded that of M4 and M5 (≤ 2.4°). Although M3 exhibited no performance degradation for Case 1 up to a certain bias magnitude, its RMSE gradually increased with increasing bias magnitude for Case 2. Additionally, the remaining four methods, except M3, exhibited similar RMSE increments in Cases 1 and 2.

Fig. 2.

(a) RMSE and (b) increment in RMSE compared with when the bias was 0°/s for Case 2 (unit: °)

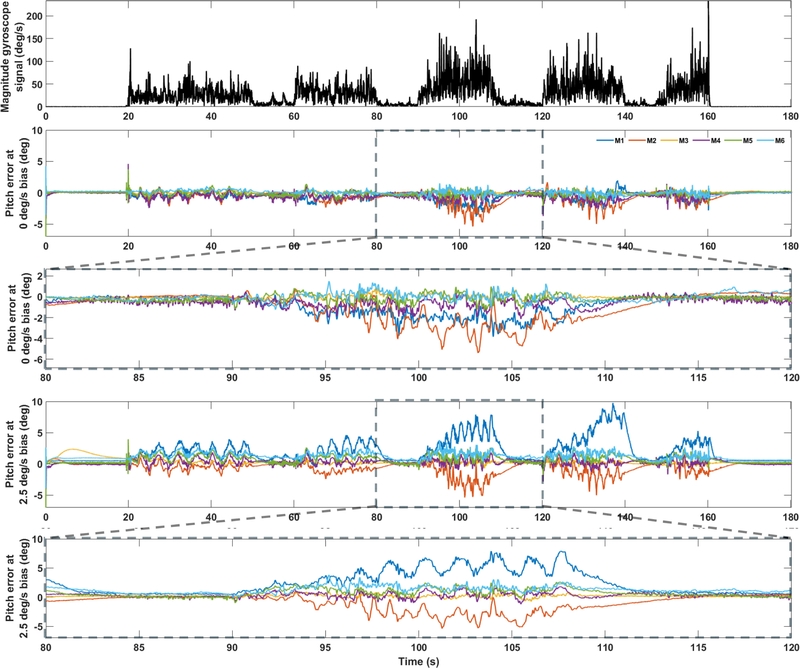
Fig. 3 shows the magnitude of the gyroscope signal and pitch error for the validation biases of 0°/s (baseline) and 2.5°/ s. Comparing the results, M1, which lacks a bias compensation mechanism, showed a drift during dynamic periods when subjected to a bias of 2.5°/s.

Fig. 3.

Pitch errors and magnitudes of the gyroscope signals of the data

4.2 Discussions

M1 estimates the vertical reference vector by applying a Markov-chain-based external acceleration model to compensate for dynamic disturbances. However, as M1 lacks a bias compensation mechanism, the estimation performance deteriorated significantly as the validation bias magnitude increased, despite its ability to correct for external acceleration. These results highlight the importance of gyroscopic bias compensation.

M2 employs a KF to estimate the gyroscope bias and external acceleration. The baseline RMSEs for Cases 1 and 2 were 2.85° and 3.36°, respectively, which were higher than the RMSE from the other methods under a validation bias of 2.5°/s. However, M2 maintained a maximum RMSE increment of only 0.02° for both Cases 1 and 2, indicating no performance degradation with increasing validation bias. Thus, M2 is robust to bias, but exhibits weak inherent estimation performance.

M3 demonstrated the best estimation performance among all the methods for both Cases 1 and 2. It maintained an RMSE increment of only 0.01° for Case 1 up to a validation bias of 2°/s, with an increment of 0.26° at 2.5°/s. This suggests that the bias compensation mechanism of M3 is designed to handle biases up to 2°/s. However, unlike in Case 1, the RMSE of M3 in Case 2 gradually increased with increasing bias magnitude. Specifically, when the bias was 2.5°/s in Case 1, the RMSE increase was 0.26°, whereas that in Case 2 was approximately doubled at 0.56°. This can be attributed to the bias compensation mechanism that estimates the bias by distinguishing between static and dynamic states, which results in a degraded compensation performance when the data are limited to static intervals. Additionally, the RMSE increment of M3 in Case 2 was comparable to or slightly larger than those of M4 and M5.

M4 and M5 had the same model structure but differed in the presence or absence of bias augmentation, and the performance improvement owing to the application of bias augmentation was not significant. However, both methods exhibited similar RMSE increments across all the validation bias magnitudes, indicating that, although bias augmentation improved the inherent estimation performance by approximately 0.15°, it did not enhance the robustness against bias.

M6 exhibited the best baseline estimation performance among the ML-based methods for Cases 1 and 2. However, the RMSE increments with increasing bias magnitude were larger than those of M4 and M5, with the maximum RMSE values of 2.29° for Case 1 and 2.59° for Case 2, indicating a weaker robustness against bias. Thus, although M6 achieves an excellent inherent estimation performance, it is less robust to bias.

By comparing rule-based algorithms with and without bias compensation mechanisms, significant performance degradation was observed in the absence of compensation, confirming that existing bias compensation mechanisms provide an effective correction for constant biases. Among the ML-based methods, M5 and M6 applied bias augmentation instead of preprocessing steps for immediate compensation to improve robustness. However, the results indicate that bias augmentation does not enhance robustness. Furthermore, given that the RMSE increase of M6 was greater than that of M4, it is suspected that bias augmentation may degrade robustness. This suggests that, while bias augmentation improves the inherent estimation performance, it does not contribute to robustness. One reason for this is presumed to be that models with bias augmentation, which are trained with biases within a specific range, may experience further degradation in actual estimation performance when subjected to validation biases larger than the training range. Additionally, further analysis is required on factors, such as the bias magnitude used for augmentation, the ratio of augmented data to original data, and other training parameters, to understand the difference in robustness between M5 and M6.

All ML-based methods directly utilize gyroscope signals with bias as the input data, without any explicit bias compensation. Nevertheless, compared with M1, a rule-based algorithm without a bias compensation mechanism, the ML-based methods exhibited significantly higher robustness. This can be attributed to the fundamental differences in the estimation approaches. While rule-based algorithms rely on strapdown integration, which is susceptible to drift owing to accumulated errors, ML-based methods estimate attitudes using parameters learned from temporal patterns in time-series data. Consequently, it can be inferred that the ML-based methods inherently exhibit greater robustness.

Overall, ML-based methods demonstrated greater robustness than rule-based methods without a bias compensation mechanism. However, when a bias compensation mechanism is applied to a rule-based method, it exhibits higher robustness than ML-based methods.

Rule-based methods explicitly estimate the bias and compensate for it (i.e., estimate and remove it from gyroscope signals). For example, M3 applies a bias estimation KF, where the KF directly uses gyroscope signals as bias measurements under static conditions and estimates the bias using the rotation matrix and accelerometer signals under dynamic conditions. In contrast, ML-based methods apply gyroscope signals with bias as input data during the training process. This exposes the model to bias, enabling it to learn and adjust accordingly while selecting parameters that produce the optimal attitude. Thus, in ML-based methods, bias robustness is reinforced in the model through an implicit approach. For the time-constant bias addressed in this study, rule-based methods explicitly applying bias compensation mechanisms demonstrated superior performance compared with ML-based methods utilizing the implicit compensation approach. However, additional comparisons are required for the time-varying biases.

A detailed analysis of rule-based algorithms reveals that M2 exhibits superior robustness across all data types, but a poor estimation performance under bias-free conditions. By contrast, M3 demonstrated better estimation performance under bias-free conditions and superior robustness in Case 1. However, its robustness for Case 2 was comparable to or slightly lower than that of M4 and M5. This suggests that, in Case 2, ML-based methods may contribute more to the robustness than bias compensation mechanisms, as in M3. Therefore, further studies on bias compensation and attitude estimation using ML-based methods are required. Additionally, as this study focused solely on constant-bias validation, further validation is required for time-varying gyroscope bias components, such as in-run bias or temperature-induced bias variations.

5. CONCLUSIONS

This study compared and analyzed the robustness of ruleand ML-based attitude estimation methods against gyroscopic bias. The validation results showed that the robustness of the rule-based algorithms improved significantly owing to the bias compensation mechanism. In contrast, for the ML-based approaches, bias augmentation slightly improved the estimation performance, but resulted in similar or worse robustness. Rule-based algorithms without a bias compensation mechanism exhibited lower robustness than ML-based algorithms. However, once a bias compensation mechanism was applied, rule-based algorithms demonstrated superior robustness compared with ML-based methods.

However, the best-performing rule-based algorithm (M3) was less robust in Case 2 than in Case 1. Specifically, when the bias was 2.5°/s, the RMSE increment in Case 2 was approximately twice that in Case 1. This suggests that the bias compensation mechanism significantly contributes to the robustness against constant bias in data that include static intervals (Case 1); however, its contribution is somewhat lower in data without static intervals (Case 2). Therefore, rule-based methods with bias compensation mechanisms are suitable for general fields that require attitude estimation technologies. However, even effective bias compensation mechanisms may exhibit reduced compensation performance under prolonged dynamic conditions, as in Case 2. Thus, it may be worth considering the use of ML-based methods for applications, such as aircraft or ships, exposed to dynamic conditions during longterm operations. These findings provide insight into the performance stability and reliability of attitude estimation methods when processing data affected by biases.

As the findings of this follow-up study are limited to the validation of constant bias, additional studies are required to evaluate the robustness of attitude estimation methods against time-varying bias components. In ML-based methods, bias augmentation contributes less to robustness than the bias compensation mechanism in rule-based algorithms. Accordingly, to achieve a higher estimation performance, ML-based methods may also need to explore alternative approaches to compensate for gyroscopic bias.

Acknowledgments

This study was supported by the Korea Research Institute for Defense Technology Planning and Advancement (KRIT) grant funded by the Korean government (DAPA (Defense Acquisition Program Administration)) (No.20-302-H00-002(KRITCT-22- 070), Development of Next-Generation Non-Laser-Based MILES, 2022).

References

C.V. Angelino, V.R. Baraniello, L. Cicala, UAV position and attitude estimation using IMU, GNSS and camera, Proceedings of 2012 15th International Conference on Information Fusion, Singapore, 2012, pp. 735–742.
S.R. Bassolillo, E. D’Amato, I. Notaro, G. Ariante, G. Del Core, M. Mattei, Enhanced attitude and altitude estimation for indoor autonomous UAVs, Drones 6 (2022) 18. [https://doi.org/10.3390/drones6010018]
C. Eling, L. Klingbeil, H. Kuhlmann, Real-time singlefrequency GPS/MEMS-IMU attitude determination of lightweight UAVs, Sensors 15 (2015) 26212–26235. [https://doi.org/10.3390/s151026212]
H. Ahmed, M. Tahir, Accurate attitude estimation of a moving land vehicle using low-cost MEMS IMU sensors, IEEE Trans. Intell. Transp. Syst. 18 (2016) 1723–1739. [https://doi.org/10.1109/TITS.2016.2627536]
H.G. de Marina, F. Espinosa, C. Santos, Adaptive UAV attitude estimation employing unscented Kalman filter, FOAM and low-cost MEMS sensors, Sensors 12 (2012) 9566–9585. [https://doi.org/10.3390/s120709566]
Á. Odry, R. Fullér, I.J. Rudas, P. Odry, Kalman filter for mobile-robot attitude estimation: Novel optimized and adaptive solutions, Mech. Syst. Signal Process. 110 (2018) 569–589. [https://doi.org/10.1016/j.ymssp.2018.03.053]
H. Ren, P. Kazanzides, Investigation of attitude tracking using an integrated inertial and magnetic navigation system for hand-held surgical instruments, IEEE/ASME Trans. Mechatron. 17 (2010) 210–217. [https://doi.org/10.1109/TMECH.2010.2095504]
N. Antigny, M. Servières, V. Renaudin, Pedestrian track estimation with handheld monocular camera and inertialmagnetic sensor for urban augmented reality, Proceedings of 2017 International Conference on IPIN, Sapporo, Japan, 2017, pp. 1–8. [https://doi.org/10.1109/IPIN.2017.8115934]
Z. Wu, D. Yuan, F. Zhang, M. Yao, Low-cost attitude estimation using GPS/IMU fusion aided by land vehicle model constraints and gravity-based angles, IEEE Trans. Intell. Transp. Syst. 23 (2021) 13386–13402. [https://doi.org/10.1109/TITS.2021.3124060]
J.K. Lee, E.J. Park, S.N. Robinovitch, Estimation of attitude and external acceleration, IEEE Trans. Instrum. Meas. 61 (2012) 2262–2273. [https://doi.org/10.1109/TIM.2012.2187245]
D. Roetenberg, H.J. Luinge, C.T. Baten, P.H. Veltink, Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation, IEEE Trans. Neural Syst. Rehabil. Eng. 13 (2005) 395–405. [https://doi.org/10.1109/TNSRE.2005.847353]
D. Laidig, T. Seel, VQF: Highly accurate IMU orientation estimation with bias estimation and magnetic disturbance rejection, Inf. Fusion 91 (2023) 187–204. [https://doi.org/10.1016/j.inffus.2022.10.014]
F. Edrisi, V.J. Majd, Attitude estimation of an accelerated rigid body with sensor fusion based-on switching extended Kalman filter, Proceedings of 2015 AI and Robotics IRANOPEN 2015–5th Conference on Artificial Intelligence and Robotics, Qazvin, Iran, 2015, pp. 1–6. [https://doi.org/10.1109/RIOS.2015.7270737]
A. Jouybari, H. Amiri, A.A. Ardalan, N.K. Zahraee, Methods comparison for attitude determination of a lightweight buoy by raw data of IMU, Measurement 135 (2019) 348–354. [https://doi.org/10.1016/j.measurement.2018.11.061]
D. Weber, C. Gühmann, T. Seel, RIANN—A robust neural network outperforms attitude estimation filters, AI 2 (2021) 444–463. [https://doi.org/10.3390/ai2030028]
J.S. Choi, C.J. Lee, J.K. Lee, A parallel recurrent neural network for robust inertial and magnetic sensor-based 3D orientation estimation, IEEE Access, 11 (2023) 89685– 89693. [https://doi.org/10.1109/ACCESS.2023.3305990]
J.Y. Huang, Z.Y. Huang, K.H. Chen, Combining low-cost inertial measurement unit (IMU) and deep learning algorithm for predicting vehicle attitude, Proceedings of 2017 IEEE Conference on Dependable and Secure Computing, Taipei, Taiwan, 2017, pp. 237–239. [https://doi.org/10.1109/DESEC.2017.8073847]
P. Narkhede, R. Walambe, S. Poddar, K. Kotecha, Incremental learning of LSTM framework for sensor fusion in attitude estimation, PeerJ Comput. Sci. 7 (2021) e662. [https://doi.org/10.7717/peerj-cs.662]
A.E. Mahdi, A. Azouz, A.E. Abdalla, A. Abosekeen, A machine learning approach for an improved inertial navigation system solution, Sensors 22 (2022) 1687. [https://doi.org/10.3390/s22041687]
M.L. Hoang, A. Pietrosanto, New artificial intelligence approach to inclination measurement based on MEMS accelerometer, IEEE Trans. Artif. Intell. 3 (2021) 67–77. [https://doi.org/10.1109/TAI.2021.3105494]
A.A. Golroudbari, M.H. Sabour, End-to-end deep learning framework for real-time inertial attitude estimation using 6DOF IMU, arXiv, https://arxiv.org/abs/2302.06037, (2023).
J.S. Choi, J.K. Lee, Effects of Data Augmentation on the Nine-Axis IMU-Based Orientation Estimation Accuracy of a Recurrent Neural Network, Sensors 23 (2023) 7458. [https://doi.org/10.3390/s23177458]
L. Perez, J. Wang, The effectiveness of data augmentation in image classification using deep learning, arXiv, https://arxiv.org/abs/1712.04621, (2017).
C. Shorten, T.M. Khoshgoftaar, A survey on image data augmentation for deep learning, J. Big Data 6 (2019) 1–48. [https://doi.org/10.1186/s40537-019-0197-0]
S. Y. Feng, V. Gangal, J. Wei, S. Chandar, S. Vosoughi, T. Mitamura, et al., A survey of data augmentation approaches for NLP, arXiv, https://arxiv.org/abs/2105.03075, (2021) [https://doi.org/10.18653/v1/2021.findings-acl.84]
J. Wei, K. Zou, Eda: Easy data augmentation techniques for boosting performance on text classification tasks, arXiv, https://arxiv.org/abs/1901.11196, (2019). [https://doi.org/10.18653/v1/D19-1670]
L. Tran, D. Choi, Data augmentation for inertial sensorbased gait deep neural network, IEEE Access 8 (2020) 12364–12378. [https://doi.org/10.1109/ACCESS.2020.2966142]
C. Li, K.K. Tokgoz, M. Fukawa, J. Bartels, T. Ohashi, K.- I. Takeda, et al., Data augmentation for inertial sensor data in CNNs for cattle behavior classification, IEEE Sens. Lett. 5 (2021) 1–4. [https://doi.org/10.1109/LSENS.2021.3119056]
A. Jaafer, G. Nilsson, G. Como, Data augmentation of IMU signals and evaluation via a semi-supervised classification of driving behavior, Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 2020, pp. 1–6. [https://doi.org/10.1109/ITSC45102.2020.9294496]