GMR센서 배열을 이용한 자석팁의 2D 위치 추정

1. 서 론

불투명한 물체나 공간 속에 금속 조각이 놓여 있을 때 바깥에서 이것을 확인하기 위해 사용하는 방식으로 X선, 자기장, 초음파 등이 있다. 특히 사람 몸속에 가이드와이어나 카테터와 같은 물체를 넣어 시술을 할 경우 카테터의 위치를 확인하기 위해 X 선이 가장 널리 이용되고 있다. 하지만 이는 해당 시술을 반복적으로 진행하는 환자와 시술자의 건강에 피해를 줄 염려가 있으므로 초음파, 자기장 등을 이용하여 대체할 수 있는 방법을 찾고자 하는 노력이 시도되어 왔다[1,2]. 초음파는 뼈와 같은 장애물이 중간에 있으면 초음파가 제대로 전달되지 않아 금속 조각을 검출할 수 없지만 자기장은 방해받지 않고 검출할 수 있다. 이러한 장점 때문에 비접촉식 위치 감지가 필요한 분야 – 제스쳐를 사용한 인터페이스, 3D 마우스 등 - 에 자성체를 넣어 적용되고 있다[3-5].

본 연구에서는 카테터를 이용한 의료시술시 자기 센서인 GMR (Giant magneto resistance) 센서를 이용하여 자석팁이 부착된 가이드와이어나 카테터를 인체에 삽입하여 시술할 때 끝단의 위치를 추정하는 방법을 제시하고자하였다. GMR 센서는 빠른 응답성과 높은 감도를 가지고 있어 하드디스크 드라이브, 바이오센서 등의 여러 산업 분야에 사용되고 있다[6-8]. 실험을 통해 GMR 센서의 출력전압과 거리 관계식을 구하고, 2차원 XY평면으로 확장하여 전압과 거리를 등고선으로 표현하였다. 이를 근거로 해서 XY평면에 놓인 자석팁의 위치를 추정하는 알고리즘을 개발하고 성능실험을 통해 시스템의 유효성을 확인하였다.

2. GMR 센서를 이용한 자기장 검출

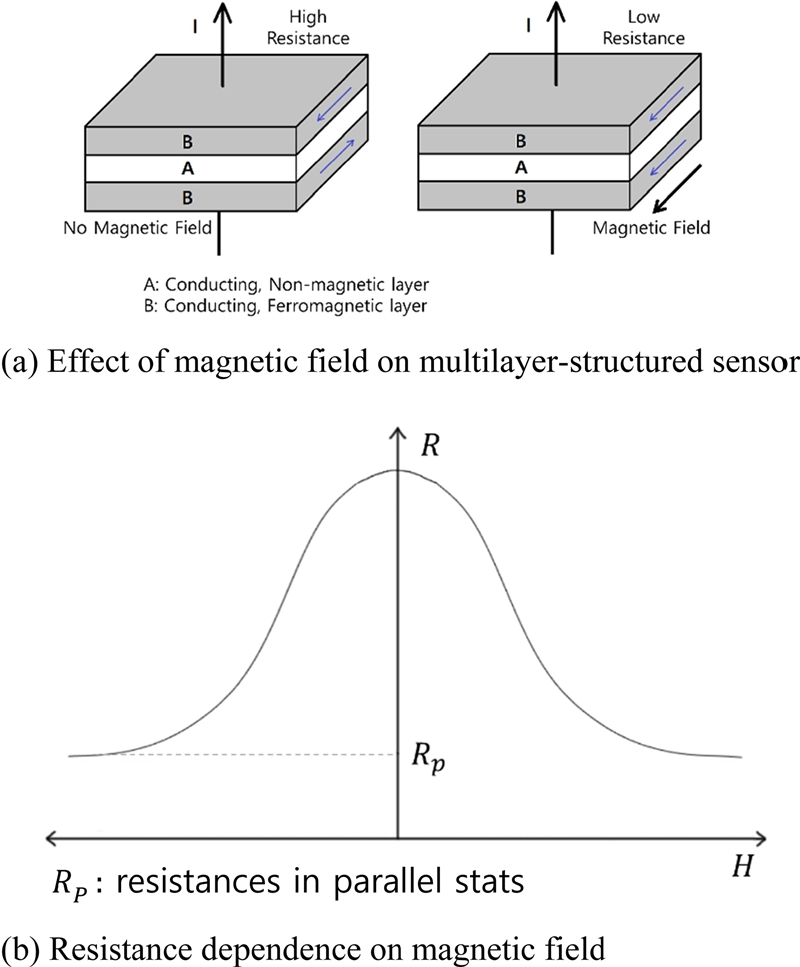
2.1 GMR 센서

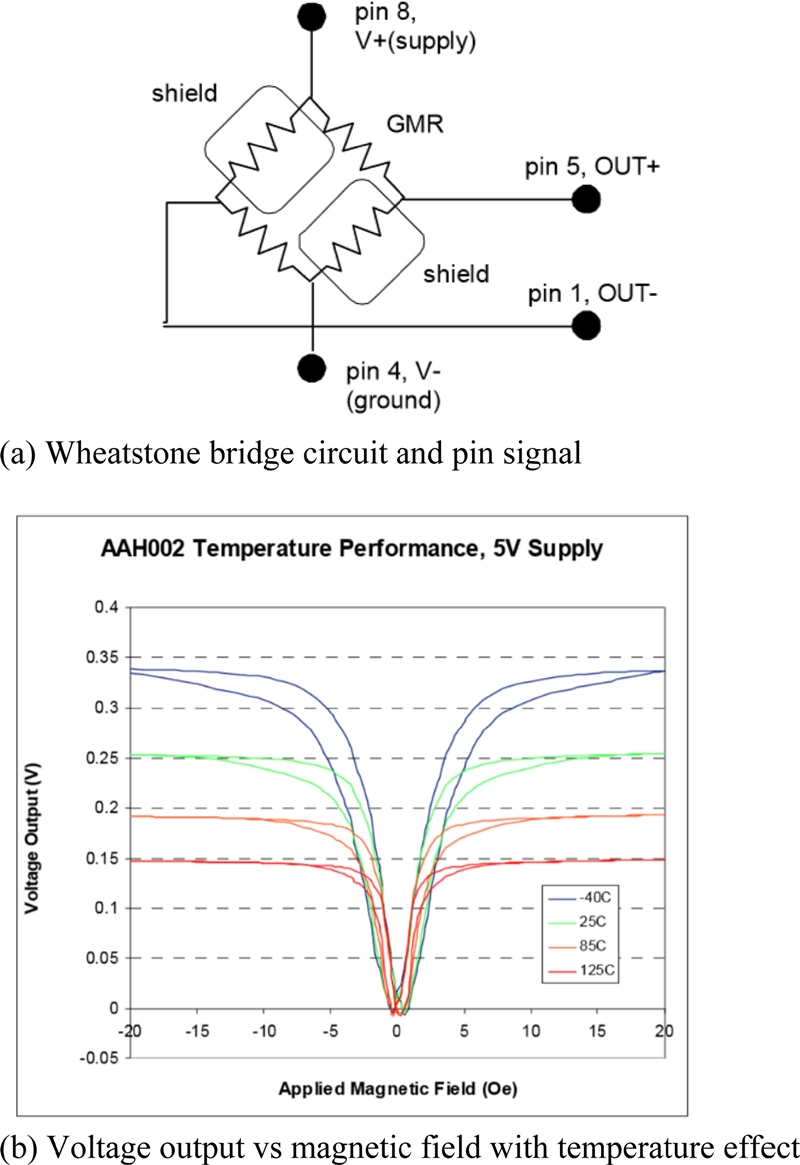
GMR센서는 Fig. 1(a) 처럼 강자성체와 비자성체의 다층평면으로 이루어진 구조로서 자기장의 유무와 크기에 따라 Fig. 1(b)와 같이 자성체의 자기극성 모멘트 소자(magnetic dipole moments)가 정렬을 달리함으로써 저항 변화를 일어키는 현상을 이용하는 센서이다[9]. 본 연구에서 사용한 GMR센서(AAH-002(NVE사))는 Fig. 2(a)의 휘트스톤 브리지 구조로 되어 있어, 자기장에 의하여 생긴 센서의 저항 변화가 출력단 핀1, 5의 전압으로 출력된다. 자기장에 따른 출력전압은 Fig. 2(b)와 같이 포화되기 전의 선형구간에서 사용할 수 있는데 환경 온도가 높을수록 출력이 줄어들어 측정정밀도가 떨어진다. Table 1은 이 센서의 성능특성을 나타낸다.

Fig. 1.

Structure and working principle of GMR sensor

Fig. 2.

Technical data of a GMR sensor (AAH002-02)

Table 1.

Performance characteristics of GMR sensor (AAH002-02)

2.2 자석에서 거리에 따른 자기장 세기와 GMR 센서 출력전압

자석 주변에 생성되는 자기장의 세기는 거리와 방향에 의해 Biot-Savart 식으로 표현된다. 크기가 작은 자석의 중심에서 r위치에 있는 점에서 자기장 세기를 Biot-Savart식으로 표현 하면 식(1)과 같다[10].

$\[ \overrightarrow{\mathrm{B}}\left(\overrightarrow{\mathrm{m}},\overrightarrow{\mathrm{r}}\right)=\frac{{\mathrm{\mu }}_0}{4\mathrm{\pi }}\frac{{\mathrm{r}}^2\overrightarrow{\mathrm{m}}-3\overrightarrow{\mathrm{r}}\left(\overrightarrow{\mathrm{r}}\times \overrightarrow{\mathrm{m}}\right)}{{\mathrm{r}}^5}+{\overrightarrow{\mathrm{B}}}_{\mathrm{E}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{h}} \]$

(1)

2.2.1 자석 축과 센서 축이 일직선인 경우

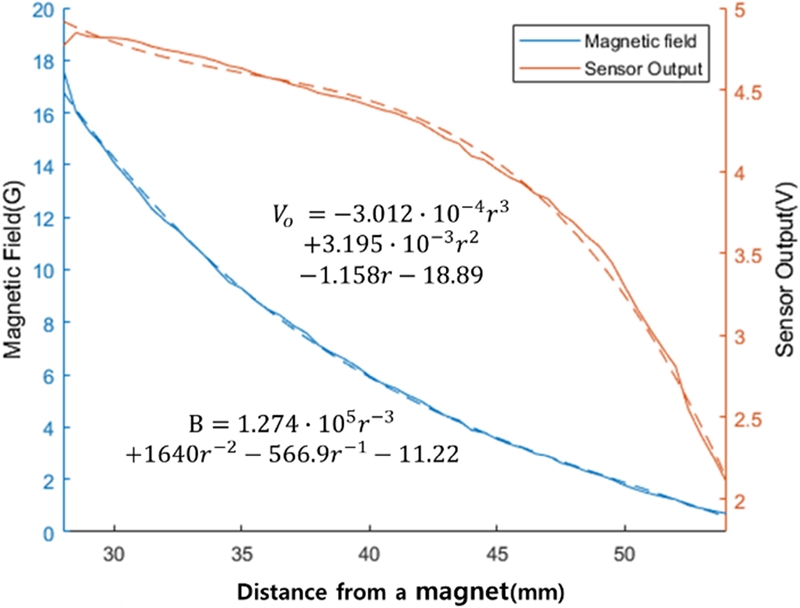
자석을 원통(지름 8.3 mm, 높이 3.2 mm, 표면 자석세기 900 Oe) 형 페라이트 자석으로 하고, 자석과 측정기 축을 일치시켜 축의 영향은 없애고, 자기측정기와 GMR 센서를 이용해 자기장 세기와 GMR 센서의 출력전압이 거리에 따라 어떻게 변하는지 조사하였다. Fig. 4는 거리 변화에 따른 자기장 세기와 출력전압을 나타낸다. 최대 감지 거리는 55 mm 정도이고, 자기장 세기는 거리가 증가함에 따라 지수함수적으로 감소하지만 출력전압은 그 반대 형태로 감소한다. 이것은 GMR 센서 출력이 Fig. 2(b)의 성능곡선에 따라 자기장 세기가 클 때 변화율이 작아지는 성질에 기인한 것이다. 이들을 근사식으로 표현하면 각각 식(2), 식(3)과 같이 거리의 3차 다항식으로 된다. Fig. 3은 자기장B, 거리벡터r, 자기쌍극자모멘트m의 관계를 나타냈다.

$\[ \mathrm{B}=1.274\cdot {10}^5{r}^{-3}+1640r^{-2}-566.9r^{-1}-11.22 \]$

(2)

$\[ V_o=-3.012\cdot {10}^{-4}{r}^3+3.195\cdot {10}^{-3}{r}^2-1.158r-18.89 \]$

(3)

Fig. 3.

Magnetic field B due to distance r and dipole m

Fig. 4.

Magnetic field and sensor output according to distance from a magnet

2.2.2 자석 축과 센서 축이 직각인 경우

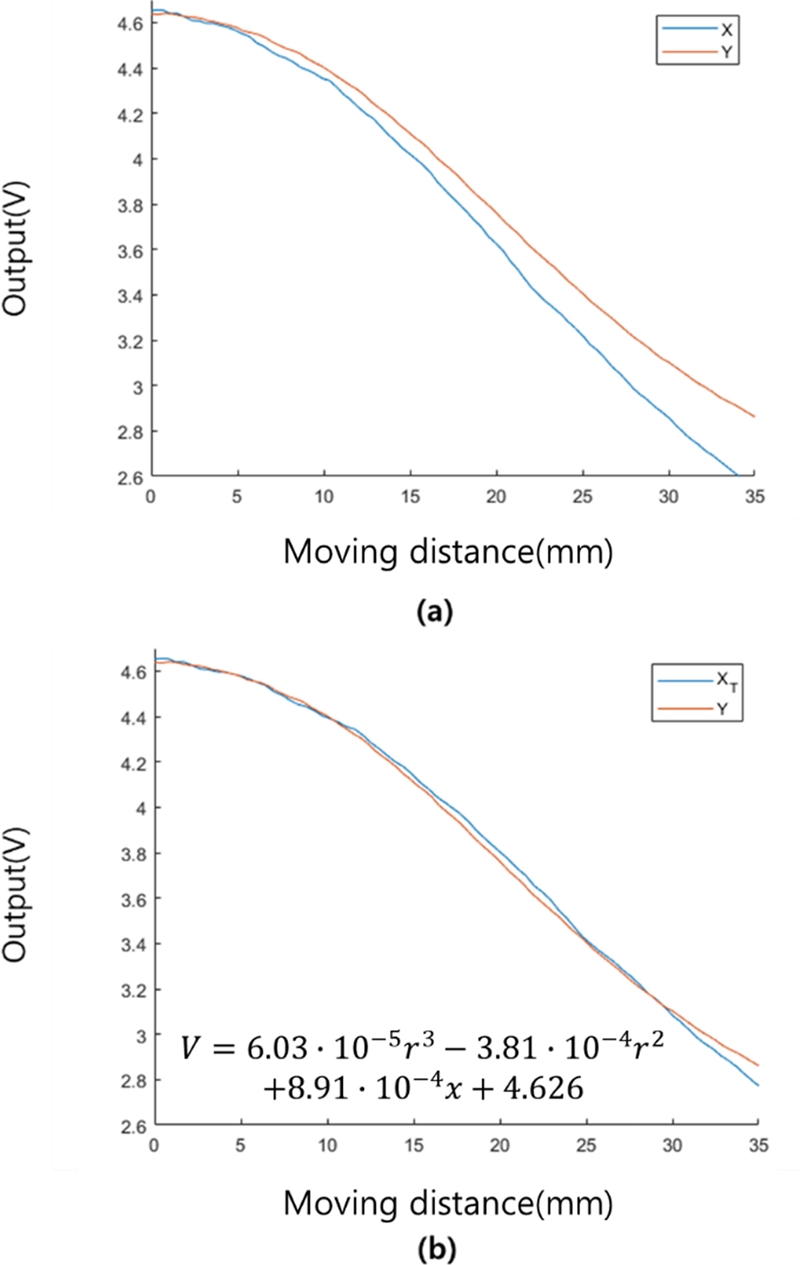
자석 축과 센서 축이 직각인 경우 자석팁이 센서와 수직 거리 30 mm떨어진 평면에서 X 축, Y축으로 각각 이동하면서 GMR 센서 출력전압을 측정하였다. 그 결과는 Fig. 5(a)에 보이는 것처럼 약간 다르게 나타났는데 이것은 방향의 영향으로 생각된다. 최대 감지거리는 X축 방향으로 33 mm, Y축 방향으로는 38 mm였다. 같은 출력이더라도 축에 따라 추정 거리가 달라지는 문제점을 해결하기 위하여 아래와 같은 알고리즘으로 좌표 정규화를 시행하였다[11].

Fig. 5.

Normalization of output difference due to moving direction - X, Y : (a) XY plane, (b) XTY plane

Y축을 기준으로 X의 변환축을 XT축이라 X와 X_T의 관계는 다음 식과 같고, Fig. 5(a)는 Fig. 5(b)처럼 변환된다.

$\[ \mathrm{X}=0.89\cdot X_r \]$

(4)

변환 후 Fig. 5(b)의 곡선을 전압-거리 근사식으로 표현하면 각각 식(5)와 같이 거리의 3차 다항식으로 된다.

$\[ V=6.03\cdot {10}^{-5}{r}^3-3.81\cdot {10}^4{r}^2+8.91\cdot {10}^{-4}r+4.626 \]$

(5)

3. 행렬 센서를 이용한 자석팁의 2차원 위치 추정

3.1 2x2행렬센서와 자석팁의 구성

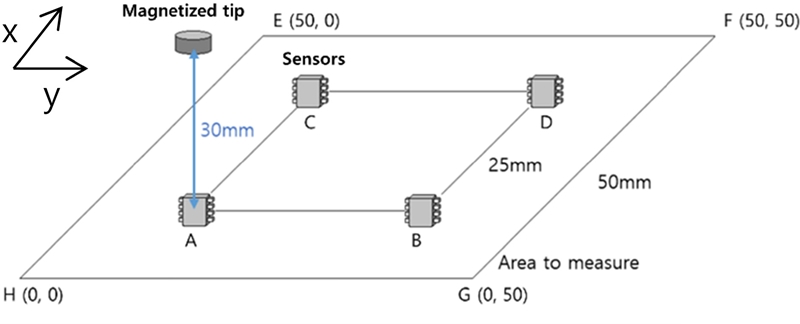
식(5)를 이용하면 GMR 센서의 출력전압으로 자석팁까지의 거리를 추정할 수 있다. 본 연구에서는 센서를 XY 평면 위 각축에 두 개씩 행렬(2x2)로 배치하여 4개 센서의 출력전압을 이용해 행렬 내의 자석팁 위치를 추정하고자 한다[12]. 측정 범위를 고려하여 센서를 25 mm 간격으로 하여 Fig. 6처럼 행렬센서와 자석팁의 배치하였다. 센서가 놓이는 위치 A, B, C, D는 Table 2와 같고, 검출할 수 있는 자석팁의 이동공간은 EFGH이다. 자석팁은 센서가 배열된 평면으로부터 평행하게 30 mm 떨어진 평면 위에서 이동한다.

Fig. 6.

Configuration of 2x2 array sensors and a magnet tip

Table 2.

Coordinates of each sensor position

3.2 2차원 이동 실험장치

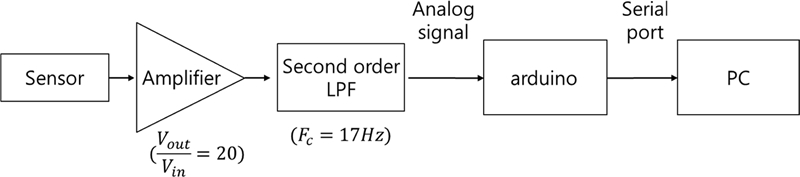
Fig. 7에 보이는 것처럼 제작된 2×2행렬 센서는 Z축 방향을 향하도록 고정되어 있다. 자석은 행렬 센서 평면에서 30 mm떨어진 위치에 있는 스텝 모터 구동 XY 스테이지에 얹혀 X 또는 Y축으로 이동된다. 자석의 방향은 N극을 띄는 면이 센서 평면 방향을 바라보도록 하였다.

Fig. 7.

Experimental setup comprised of 2x2 array sensor, magnet tip and XY stage

3.3 신호처리 장치 구성

Fig. 8은 GMR 센서 신호를 PC에서 받아들이는 신호처리과정을 나타낸다. 각 센서의 출력전압은 증폭과 필터 과정을 거쳐서 아두이노를 통해 측정하고, 수집된 데이터는 시리얼 데이터통신을 PC에 전송된다. 전송된 4개의 센서 데이터를 이용해서 최종 좌표를 추정한다.

Fig. 8.

Signal processing for acquisition of each GMR sensor output

4. 위치 추정 시스템의 성능 평가

4.1 자석팁의 위치에 따른 센서출력

자석팁을 XY 스테이지로 각 축으로 이동하면서 375 μm 간격마다 출력전압을 측정하였다. Fig. 9은 한 개의 센서가 자석팁의 XY위치에 따라 취득한 출력전압(V)을 Z축 높이로 나타낸 것이다. 센서에 자석이 가까울수록 출력이 높고, 멀어질수록 작아지는 종 모양을 확인할 수 있다. 이처럼 출력한 그래프를 각 센서마다 XY 평면에서 등고선으로 표시한 것이 Fig. 10이다. 각 센서 위치에 자석팁이 있으면 출력전압이 가장 크고, 등고선의 중심에 해당한다.

Fig. 9.

Bell-shaped sensor output versus XY position of a magnet tip

Fig. 10.

Contour map representation of each sensor output with different colors corresponding to outputs; (a) sensor 1, (b) sensor 2, (c) sensor 3, (d) sensor 4

4.2 센서 출력을 이용한 자석팁의 거리 추정

Fig. 11은 미리 교정해 둔 센서 출력과 거리의 관계식을 나타내는데, 이런 데이터베이스를 기반으로 센서의 출력에 따라 거리를 추정할 수 있다. 이는 거리에 따른 출력 전압인 식(5)의 역함수이다.

Fig. 11.

Calibrated relationship between distance and sensor output

4.3 등고선 교점을 이용한 자석팁의 위치 추정

1개 센서의 출력으로는 거리를 추정할 수 있으므로 등고선의 한 개 원주상에 자석팁이 있다고 보고, 4개 센서의 출력으로 해당 등고선들의 교점을 구하면 최종 위치를 추정할 수 있다. 측정값이 이론에 따라 정확하게 구해진다면 Fig. 12(a)와 같이 모든 등고선은 한점을 지날 것이다. 그러나 실제는 오차가 포함되므로 Fig. 12(b) 와 같이 한점에서 만나지 않는다. 본 연구에서는 이를 고려하여 최적화된 교점을 이용한 위치 추정 알고리즘을 제시하였다.

Fig. 12.

Intersection points of contour circles with each estimated distance for location estimation; (a) Ideal, (b) With measurement errors, (c) Enlarged dotted area

각 센서출력으로 자석팁까지의 거리를 추정한 뒤, 각 센서를 중심으로 4개의 원형 등고선을 그리고 이들의 교점을 계산한다. 센서 n의 추정거리를 R_n 이라 하면 자석팁은 센서좌표(x_n, y_n)를 중심으로 하고 반지름이 R_n 인 원주상에 한 점(x,y)이라고 볼 수 있으므로 식 (6)처럼 나타낼 수 있다.

$\[ {\left(x-x_n\right)}^2+{\left(y-y_n\right)}^2=R_n^2 \]$

(6)

자석팁이 4개 행렬 센서로 이루어진 4각형 내부에 있다고 하면 Fig. 12(c)에 보이듯이 센서1과 센서 2, 센서2과 센서 3의 교점P12(x₁, y₁), P23(x₂, y₂)과 센서5와 센서 2, 센서 4과 센서 3의 교점P24(x₃, y₃), P34(x₄, y₄)이 자석팁의 추정 위치인데 이들을 평균한 좌표점이 통계적으로 가장 확률이 높은 자석팁의 위치가 되므로 최종 추정 좌표값은 식 7과 같다.

$\[ \mathrm{p}=\left(\frac{x_1+x_2+x_3+x_4}{4},\frac{y_1+y_2+y_3+y_4}{4}\right) \]$

(7)

4.4 자석팁 위치별 추정실험 결과

Table 3은 측정 범위 내 다양한 위치에서의 위치 추정을 실시하였을 때 각 좌표마다 가지는 추정위치와 오차를 정리하였다. 위치 추정을 진행하였을 때 일반적으로 1 mm내외의 직선오차를 가진다. 이는 위치 추정을 통하여 실제위치의 확인 가능하다고 보여진다. 가까울 수 록 출력이 센서의 포화 출력에 근접하여 중앙에 비하여 큰 오차를 가진다. 이는 자석팁이 적절한 자기장을 갖는 거리에 있을 때 높은 신용도의 결과를 내는 것을 확인 할 수 있다. 추가적인 센서의 배치로 추정 거리 오차가 교정될 수 있으며 더 넓은 범위의 위치 추정도 가능하다.

Table 3.

Error of location estimation experiment

5. 결 론

본 논문에서는 2×2 배열 GMR 센서를 사용하여 평면에서 이동하는 자석팁의 위치를 추정하는 시스템을 설계하여 성능을 분석하였다. 이를 통해 얻은 결론은 다음과 같다.

(1) Biot-Savart 식이 보이는 것처럼 자기장의 세기는 자석팁까지 거리의 -3차 다항식으로 표현되고, GMR센서의 출력전압은 거리의 3차 다항식으로 나타났다.

(2) 표면 자석세기 900 Oe인 자석 축에 일직선 운동일 때 GMR 센서의 최대 감지거리는 55 mm 이고, 30 mm 떨어진 수직운동일 때 최대 감지거리는 X축 ±33 mm, Y축 ±38 mm 이다.

(3) 4개 배열 센서의 등고선 교점으로 추정한 위치좌표는 실제위치와 최대 1.5 mm 오차내에 근접하였다.

Acknowledgments

본 연구는 부산산업과학혁신원의 지역특화 기술개발·확산 개방형연구실 운영사업의 일환으로 수행된 결과입니다.

References

• M. H. Kang “An Ultrasonic Positioning System Using Zynq SoC”, The Transactions of the Korean Institute of Electrical Engineers., Vol. 66, No. 8, pp. 1250-1256, 2017.
• T. B. Lee and H. S. Kang, “Material Estimation Method Using Dual-Energy X-Ray Image for Cargo Inspection System”, Journal of the Korea Industrial Information Systems Research., Vol. 23, No. 1, pp. 1 - 12, 2018.
• D. Hong and W. Woo, “Recent research trend of gesture-based user interfaces”, Telecommun. Rev., Vol. 18, No. 3, pp. 403-413, 2008.
• C. D. Natali, M. Beccani, and P. Valdastri, “Real-Time Pose Detection for Magnetic Medical Devices”, IEEE Transac. Magn., Vol. 49, No. 7, pp. 3524 - 3527, 2013. [https://doi.org/10.1109/TMAG.2013.2240899]
• J. Daughton, J. Brown, E. Chen, R. Beech, A. Pohm, and W. Kude, “Magnetic field sensors using GMR multilayer”, IEEE Transac. Magn., Vol. 30, No. 6, pp. 4608-4610, 1994. [https://doi.org/10.1109/20.334164]
• J. M. Daughton, “GMR applications”, J. Magn. Magn. Mater., Vol. 192, No. 2, pp. 334-342, 1999. [https://doi.org/10.1016/S0304-8853(98)00376-X]
• S. C. Mukhopadhyay, K. Chomsuwan, C. P. Gooneratne, and S. Yamada, “A Novel Needle-Type SV-GMR Sensor for Biomedical Applications”, IEEE Sens. J., Vol. 7, No. 3, pp. xx-yy, 2007. [https://doi.org/10.1109/JSEN.2007.891929]
• J. Lenz and A. S. Edelstein, “Magnetic Sensors and Their Applications”, IEEE Sens. J., Vol. 6, No. 3, pp. 631-649, 2006. [https://doi.org/10.1109/JSEN.2006.874493]
• A. Anguelouch, D. H. Reich, C. L. Chien, and M. Tondra, “Detection of ferromagnetic nanowires using GMR sensors”, IEEE Transac. Magn., Vol. 40, No. 4, pp. 2997-2999, 2004. [https://doi.org/10.1109/TMAG.2004.829316]
• V. Schlagetera, P.-A. Bessea, R. S. Popovica, and P. Kucerab, “Tracking system with five degrees of freedom using a 2D-array of Hall sensors and a permanent magnet”, Sens. Actuators A, Vol. 92, No. 1-3, pp. 37-42, 2001. [https://doi.org/10.1016/S0924-4247(01)00537-4]
• P.-H. Tichit, S. N. Burokur, and A. de Lustrac, “Waveguide taper engineering using coordinate transformation technology”, Opt. Express, Vol. 18, No. 2, pp. 767-772, 2010. [https://doi.org/10.1364/OE.18.000767]
• S. K. Kwon and D. M. Lee, “Performance Analysis of Compensation Algorithm for Localization using Equivalent Distance Rate”, J. Korea Acad. Ind. Coop. Soc., Vol. 11, No. 4, pp. 1248-1253, 2010. [https://doi.org/10.5762/KAIS.2010.11.4.1248]