유속 및 각도 측정을 위한 인공 옆줄 센서 개발

1. 서 론

연어는 산란기가 되면 태어난 곳으로 돌아가는데, 모천 회귀하는 연어의 이동 패턴을 살펴보면, 강물이 흐르는 방향으로 움직이기 보다는 비스듬하게 강물을 거슬러 이동하는 것을 알 수 있다. 이는 유체의 저항을 정면이 아닌 비스듬한 방향으로 받아 최소한의 힘으로 역류를 극복하기 위한 것이다.

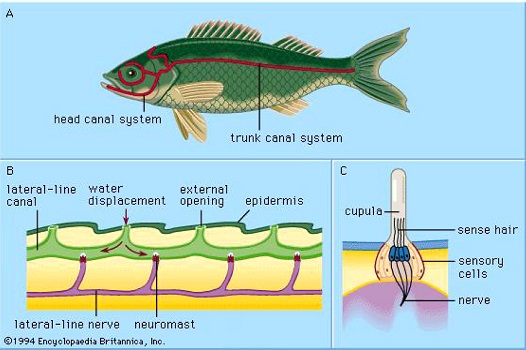
연어와 같은 물고기가 이와 같은 방식으로 이동할 수 있는 이유는 아가미와 옆줄에 있는 미세한 감각기관의 역할 때문이라는 주장이 있다. 이러한 미세감각기관은 유체의 흐름 속도와 온도를 감지하여 강물의 상류와 하류의 방향을 알 수 있으며, 특히 물고기의 옆줄은 강물의 속도를 파악하고 균형을 유지할 수 있게 해주며, 접근하는 물체를 감지하는 역할을 한다[1].

Fig. 1에서, 물고기 옆줄은 머리부터 몸통까지 구성되어 있으며 원리는 외부 구멍(external opening)의 압력 차이로 인해 운하 시스템(canal system)에 유체의 흐름이 발생하게 되고, 원형돌기(cupula)를 자극해서 측정 세포(sensory cells)에서 전기적 신호가 발생하여 유체의 흐름을 파악한다.

Fig. 1.

Structure of lateral line[2].

이러한 물고기 옆줄 원리를 모방한 여러 연구들이 진행되었다. 2002년 Zhifang Fan은 Strain Sensor를 이용하여 물고기의 Cupula 역할을 하는 센서를 개발하여, 물의 흐름이나 진동을 감지하는 연구 결과를 발표하였다[3]. 2016년 Wei Wang은 물고기 형상의 로봇 옆면에 9개의 압력센서를 배치하여 분산된 압력과 각속도를 통해 로봇의 속도를 추정하는 비선형 예측 모델을 제안하였다[4]. 2011년 Vicente I. Fernandez은 물고기가 주위 물체를 감지하는 방법에 대해 연구하였는데, 물고기의 옆줄을 모방하여 압력센서의 배열을 통해 시간에 따른 압력 데이터를 받아 주위의 움직이는 물체의 위치를 추적하였다[5].

본 논문에서는 물고기의 옆줄을 모방하여 표면의 압력 분포를 통해 흐르는 유체의 유속과 방향을 예측하는 방법에 대해서 제안하였다. 2장에서는 이론 및 시뮬레이션에 대해서, 3장에서는 실험장치 구성, 4장에서는 수류의 유속 측정, 5장에서는 수류의 방향 측정에 대해 논하고 마지막으로 결론 순으로 글을 기술하였다.

2. 이론 및 시뮬레이션

이번 장에서는 Bernoulli 방정식과 Navier-Stokes 방정식을 서술하였다. Bernoulli 방정식을 통해 속도와 압력의 관계에 대해 알 수 있으며, Navier-Stokes 방정식을 통해 형상의 압력 분포를 측정하였다. Navier-Stokes 방정식은 해석적인 해를 구할 수 없기 때문에 수치적으로 해를 구하는 CFD를 통해 압력 분포를 알아보았다.

2.3 전산유체역학(CFD)

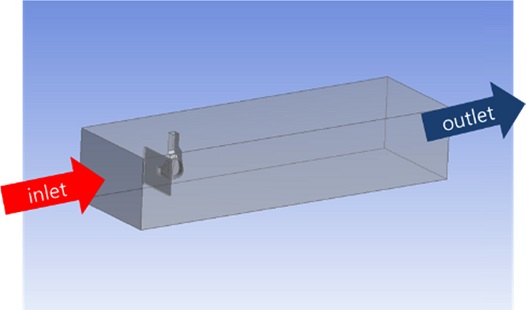
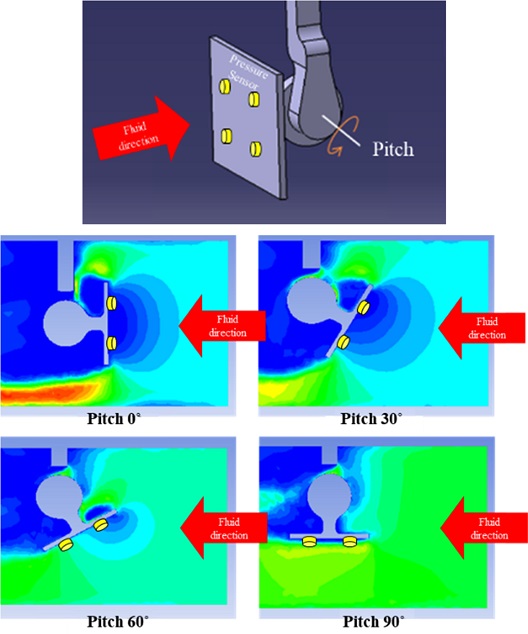
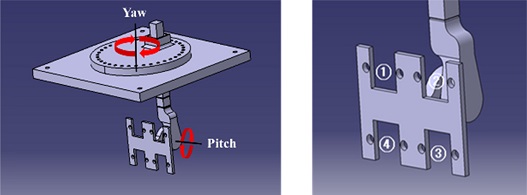
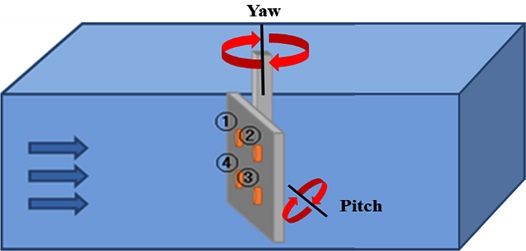
앞서 설명한 Navier-Stokes 방정식의 해를 해석적으로 구하지 못하기 때문에 CFD를 통해 근사값을 구하였다. CFD 해석 툴인 Ansys Fluent 15.0을 사용하였으며, Fig. 2와 같이 형상을 설계하여 형상의 피치(Pitch) 값을 변경하면서 총 4가지 경우에 대해 해석해 보았다.

Fig. 2.

CFD Geometric.

메쉬(mesh) 모양은 사면체(tetrahedron), 형상 주위에 인플레이션(inflation)을 주어 형상 근처의 해석을 주되게 하였으며, Table 1과 같은 경계조건을 주어 해석하였다.

Table 1.

CFD boundary condition

해석 결과 평판에서의 압력 분포는 Fig. 3와 같이 유체 방향과 수직으로 압력 분포가 형성하는 것을 알 수 있다. Pitch의 각도가 증가할수록 압력 분포의 간격이 더 크게 나타나며, 평판에 수직(피치 각도 값 0^o) 또는 수평(피치 각도 값 90^o)하게 유속이 존재할 때에는 압력 분포는 위치에 따라 압력 차이가 크지 않다는 것을 알 수 있다.

Fig. 3.

Pressure distribution according to pitch value.

3. 실험장치 구성

이번 장에서는 실험장치를 구성하는 방법에 대해 서술하였다. 본 논문에서 사용된 장치들은 크게 측정 시스템과 실험 장치로 구성되어 있다.

3.1 측정 시스템

본 논문에서 사용한 압력센서는 MS5803-01BA이다. 이는 절대값 방식 압력 센서이며, 방수를 하여 수중에 사용 가능하게 하였다. 또한 여러 센서의 데이터를 얻기 위해 Fig. 4와 같은 측정 시스템을 제작하여 실험하였다.

Fig. 4.

Measurement system diagram.

3.2 실험 장치

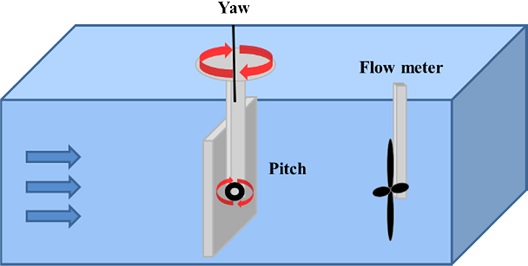
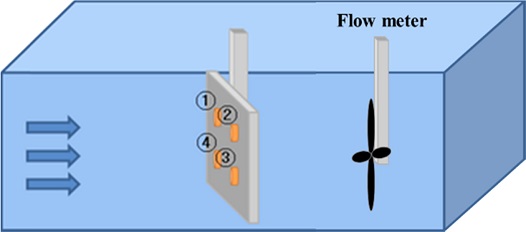
흐르는 유체의 방향과 크기를 모두 측정할 수 있도록 실험 장치는 Fig. 5와 같이 구성하였다. 유속 측정은 FLO-BTA를 사용하여 측정하였다.

Fig. 5.

Model of experimental equipment.

피치 각도 는 360^o를 10^o 마다, 요(yaw) 각도는 0^o, 30^o, 60^o, 90^o 각도를 바꿀 수 있는 실험 장치를 Fig. 6와 같이 설계 후 3D 프린터를 사용하여 제작하였다. 이 때 압력센서 사이의 간격은 가로, 세로 6 cm로 배치하였다.

Fig. 6.

Position and shape of the sensors.

3.3 실험 환경

회류 수조에서 실험을 하였으며, 실험 섹션(test section)의 크기는 0.1 × 0.15 × 1.0(m)이고 최대 유속은 약 1.2 m/s이다.

Fig. 7.

Recirculating water tank and experimental photograph.

4. 수류의 유속 측정

4.1 실험 방법

흐르는 유체의 유속을 측정하는 실험을 하기 위해, 회류 수조에 Fig. 8와 같이 4개의 압력센서를 부착시킨 평판을 달아 유속에 따라 압력센서들의 데이터 값을 측정하였다.

Fig. 8.

Experimental diagram for flow velocity measurement.

4.2 실험 결과

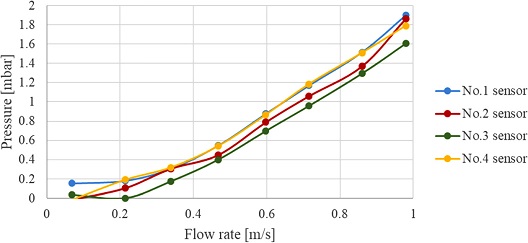
회류 수조 속 유체의 유속에 따라 평판에 부착된 4개의 압력센서의 값을 측정한 후, 운동에너지에 영향을 끼치는 압력을 구한 결과 Fig. 9와 같은 결과를 얻었다.

Fig. 9.

Data according to sensor flow rate.

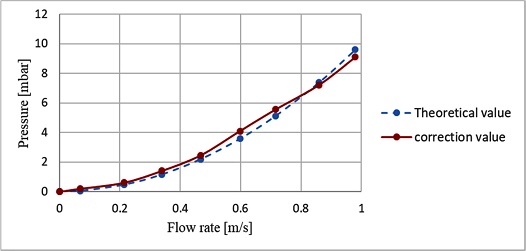
Bernoulli 방정식을 통해 유속에 따른 운동에너지와 앞서 구한 센서들의 압력을 평균하여 비교분석 하였다. 압력 값들의 측정함에 있어 손실 수두, 압력 센서 자체의 오차 및 환경적인 요소로 인한 오차가 발생하기 때문에 보정 계수를 구하여 보정한 결과 Fig. 10와 같은 데이터를 얻게 되었다.

Fig. 10.

Experimental and theoretical pressure graphs.

실험을 통해 유속에 따른 실험값이 이론 값을 잘 따라가는 것을 확인할 수 있었으며, 평판에서 4개의 절대값 방식 압력센서를 통해 흐르는 유체의 유속을 측정 가능하다는 것을 알 수 있다.

5. 수류의 방향 측정

5.1 실험 방법

Fig. 11의 그림과 같이 0.715 m/s의 일정한 유속에서 피치 각도 (0^o, 30^o, 60^o, 90°)와 요 각도 (0°, 30°, 60°, 90°) 2축의 각도를 변화시켜 총 16가지의 압력 데이터 값을 측정하였다.

Fig. 11.

Experimental diagram for measuring the direction of water flow.

5.2 실험 결과

5.2.1 평판 압력 분포 양상

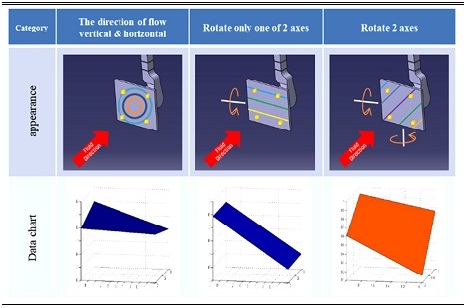
16가지의 압력 데이터 값을 분석한 결과, 다음 Table 2. Pressure distribution appearance와 같이 압력 분포 양상을 크게 3가지로 분류할 수 있다.

Table 2.

Pressure distribution appearance

(1) 유체의 방향과 수직 또는 수평인 평면

시뮬레이션에서 흐르는 유체의 방향과 수직 또는 수평인 평면은 압력 센서의 위치에서 데이터 차이가 미미한 양상을 띠고 있다. 실험에서 또한 이러한 평면에서는 압력 센서들의 데이터 차이가 작은 것을 알 수 있었다.

(2) 2축 중 한 축만 회전한 평면

한 축만 회전한 평면의 압력 분포를 보게 되면, 흐르는 유체의 방향에 수직으로 압력 분포 양상을 띠고 있다.

(3) 2축 모두 회전한 평면

두 축이 회전한 평면의 압력 분포를 보게 되면, 각 축의 회전한 각도에 따라 평면에서 형성되는 압력 분포 각도가 변하는 것을 알 수 있다.

5.2.2 방향 측정 방법

압력센서를 통해 데이터를 얻게 되면, 압력 데이터의 최댓값과 최소값의 위치에 따라 다음과 같이 3가지의 방법으로 유체의 방향을 측정한다.

(1) 압력센서 데이터의 최댓값과 최소값이 나란히 배치되어 있을 경우

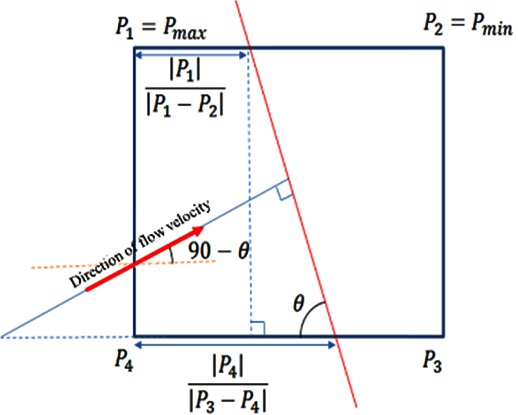
압력 센서의 극소, 극대 값이 나란히 배치되어 있으면, Table 2. Pressure distribution appearance에서 2축 중 한 축만 회전한 경우이다. 이러한 경우 와 식 (4)를 통해 유체의 방향을 측정할 수 있다.

$\[ \mathrm{\theta }={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{1}{\frac{\left|P_4\right|}{\left|P_3-P_4\right|}-\frac{\left|P_1\right|}{\left|P_1-P_2\right|}}\right] \]$

(4)

Fig. 12.

Direction of fluid measurement (1).

(2) 압력센서 데이터의 최댓값과 최소값이 마주보고 배치되어 있을 경우

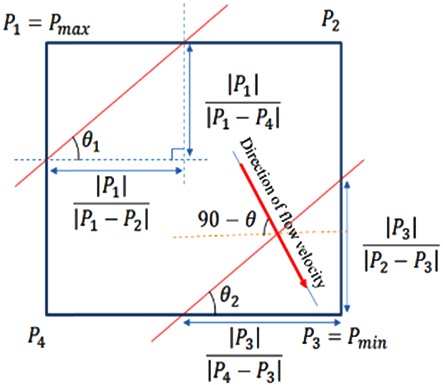
압력 센서의 극소, 극대 값이 나란히 배치되어 있으면, Table 2. Pressure distribution appearance에서 2축 모두 회전한 경우이다. 이러한 경우 Fig. 13와 식(5)를 통해 유체의 방향을 측정할 수 있다.

$\[ \begin{array}{c}{\mathrm{\theta }}_1={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{\left|P_1-P_2\right|}{\left|P_1-P_4\right|}\right],{\mathrm{\theta }}_2={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{\left|P_4-P_3\right|}{\left|P_2-P_3\right|}\right] \\ \mathrm{\theta }=\frac{{\mathrm{\theta }}_1+{\mathrm{\theta }}_2}{2}=\frac{{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{\left|P_1-P_2\right|}{\left|P_1-P_4\right|}\right]+{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{\left|P_4-P_3\right|}{\left|P_2-P_3\right|}\right]}{2}\end{array} \]$

(5)

Fig. 13.

Direction of fluid measurement (2).

(3) 임계점(Critical Point)

유체의 흐름 방향과 수직 또는 수평인 평면에서 압력 데이터를 보게 되면, 뚜렷한 경향을 보이지 않는다. 압력 데이터들의 값 차이가 유체의 방향과 수직, 수평일 때는 미미한 값을 갖게 되는 임계점을 갖게 된다. 이러한 임계점에서는 압력센서의 데이터 값이 일정한 양상을 나타내지 못하여 방향 측정에 있어 어려움이 있다.

5.2.3 각도에 따른 방향 측정 결과

앞서 각도에 따른 압력 분포 양상을 파악하였다. 유체의 방향과 수직 또는 수평인 평면의 데이터는 임계점의 위치로 데이터 양상이 뚜렷하게 보이지 않는다.

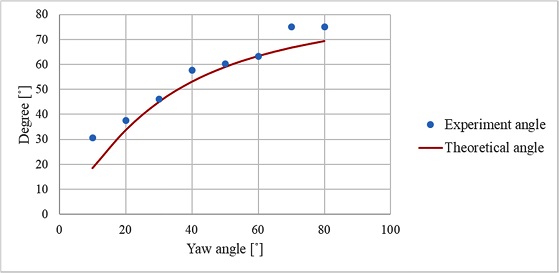
실제로 조류에서 형상들이 움직일 때에는 2축 모두 회전한 경우가 많다. 따라서 피치 각도 가 30°일 때, 요 각도를 10°단위로 증가하면서 실험해 보았다. 실험 결과는 Fig. 14과 같다.

Fig. 14.

Experimental data with increasing Yaw.

요 각도가 증가함에 따라 수류의 방향 각도가 삼각함수로 증가하는 경향을 보인다. 실험 각도가 이론 각도를 잘 따라 간다는 실험 결과를 통해 절대값 방식 압력 센서로 수류의 방향 측정이 가능하다는 것을 확인할 수 있다.

6. 결 론

본 논문에서는 절대값 방식 압력센서를 통해 흐르는 유체의 유속 및 방향을 측정하였다. 운동에너지에 영향을 끼치는 압력을 통해 유속을 측정할 수 있었으며, 평판의 압력 분포 양상을 통해 2D 방향을 측정할 수 있었다. 임계 값에서는 방향 측정에 있어 어려움 이 존재하지만, 향후 하나의 평판이 아닌 여러 평판의 배치를 통해 압력센서들의 데이터를 추출하여 2D 방향에서 3D로 흐르는 유체의 방향을 측정할 수 있을 것으로 판단된다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2019R1F1A1061706).

REFERENCES

• G. Liu, A. Wang, X. Wang, and P. Liu, “A Review of Artificial Lateral Line in Sensor Fabrication and Bionic Applications for Robot Fish”, Appl. Bionics Biomech. Vol. 2016, pp. 1-15, 2016. [https://doi.org/10.1155/2016/4732703]
• https://www.britannica.com/science/lateral-line-system, (retrieved on Jan. 28, 2021).
• Z. Fan, J. Chen, J. Zou, D. Bullen, C. Liu, and F. Delcomyn, “Design and fabrication of artificial lateral line flow sensors”, J. Micromech. Microeng, Vol. 12, No. 5, pp. 655-661, 2002. [https://doi.org/10.1088/0960-1317/12/5/322]
• W. Wang, Yuan Li, X. Zhang, Chen Wang, S. Chen and G. Xie, “Speed evaluation of a freely swimming robotic fish with an artificial lateral line”, Proc. of IEEE Int. Conf. Robot Autom., pp. 4737-4742, Stockholm, Sweden, 2016. [https://doi.org/10.1109/ICRA.2016.7487675]
• V. I. Fernandez, “Performance analysis for lateral-line-inspired sensor arrays”, Ph.D. thesis., MIT, MA, 2011. [https://doi.org/10.1575/1912/4773]
• F. White, Fluid Mechanics 8th ed., McGraw-Hill, pp. 3-58, 2016.