비분산 적외선 가스 센서 온도 보상법: 적외선 흡수도
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The motivation of this paper is to easily analyze the properties of nondispersive infrared gas sensor that has more than two different optical path length and to suggest the criterion and definition of infrared light absorbance in order to minimize the measurement errors. With the output voltage ratios and the normalized derivatives of infrared ray (IR) absorbance, when the normalized derivatives of IR absorbance decreases from 0.28 to 0.10, the lower and higher limits of errors were decreased from -5.62% and 2.39% to -4.27% and 2.78%. When the normalized derivatives of IR absorbance were 0.10, the output voltage could be partitioned into two regions with one exponential equation and the temperature compensation error was less than 5%.
Keywords:
nondispersive infrared gas sensor, IR absorbance, CO2 gas sensor, normalized derivative of IR absorbance, temperature compensation1. 서 론
국내에서 비분산 적외선 가스 센서가 실생활에 적용된 지 20여년이 흐르면서 관련된 제품의 기술은 날로 발전하고 있고, 센서를 구성하는 부품의 소형화와 첨단화에 따라 비분산 적외선 센서 또한 경박단소화 하고 있는 상태이다[1]. 적외선 램프 혹은 MEMS (Microelectromechnical Systems) 기술을 이용한 광원과 써모파일/초전형 적외선 센서는 이산화탄소 가스의 흡수 파장의 적외선을 방출하는 발광 다이오드(Light emitting diode, LED)와 적외선 광 센서(infrared photosensor)로 바뀌어졌다. 이에 따라 전체 제품의 크기가 획기적으로 축소되고, 소모 전력도 낮아져 IoT (Internet of Things) 시대에 적합한 구조를 갖게 되었다[2].
한편 비분산 적외선 가스 센서는 기본적으로 광원, 적외선 센서와 광 도파관(optical waveguide) 세 가지 구성요소로 이루어진다. 광 도파관의 형상에 따라, 혹은 측정 대상 가스와 농도에 따라, 가스가 존재하지 않는 상태에서 센서의 출력 특성은 서로 다른 함수적 특성을 보인다[3,4]. 또한 광 도파관 내에서 광 경로는 무수히 많으나, 저자를 포함하여 이들을 표준화한 두 개의 광 경로로 근사화 하여 가스의 농도에 따른 출력전압을 분석하였다. 이런 접근 방법은 가스 농도의 예측 알고리즘 작성과 적용에 오차를 제공하는 한 요인으로 작용하고 있음을 연구 결과의 사례에서 보여주고 있다[4-6].
따라서 본 논문에서는 두 개 이상의 광 경로로 표현 해석되는 비분산 적외선 가스 센서 온도 보상 방법의 새로운 기준을 제시하고자 한다. 즉, 광 흡수도의 정의와 광 흡수도의 선택 기준과 이에 따른 측정 결과의 분석을 통해 측정 오차를 줄일 수 있는 방법에 대해 제시하고자 한다.
2. 연구 방법
2.1 이론적 고찰
비분산 적외선 가스 센서는 Beer-Lambert 식에 의존한 특성을 갖으며, 이산화탄소 가스 센서의 경우, 아래에 주어진 식 (1)에 의한 가스 반응 특성을 갖고 있음이 제시되었다[7,8].
| (1) |
즉 센서의 출력 특성은 오프셋(offset)전압으로 작용하는 적외선 센서의 입력단의 광학적 필터의 특성(VBPF[V]), 대상 가스의 흡수 특성을 반영한 오프셋 전압(V4.26 μm[V]), 가스의 광학적 흡수 계수 (α[ppm-1m-1])와 광 경로(L[m])의 조합에 의해 표현된다.
그러나 광 경로가 긴 경우, 단일 광 경로에 의한 가스 반응 결과에 따른 출력 특성이 나타나는 것이 아니라, 두 개 이상의 경로와 이에 따른 출력 특성인 식 (2)로 나타낼 수 있음이 확인되었다[5-7].
| (2) |
여기서 β1, β2는 각 광 경로와 대상 가스의 흡수 계수의 곱을 의미하고, V0는 식 1)의 광학 필터에 의한 오프셋 전압, α1, α2는 각 경로상의 가스 흡수 특성을 반영한 오프셋 전압을 의미한다.
비록 식 (2)에 의해 가스 농도 (x)에 따른 출력 전압의 관계를 분석할 수 있으나, 출력 전압으로부터 미지의 가스 농도를 도출하기 위해 식(2)를 통해 산출하고, 이를 마이크로 컨트롤러(MCU)에 프로그램을 구현하는 것은 어렵기 때문에 차선의 방법이 요구되는 상태이다.
한편 Beer-Lambert 식은 입사광의 세기와 센서에 전달되는 광의 세기의 가스 흡수계수와 광 경로 의존성을 보여준다. 즉, 식 (3)과 같이 가스의 존재 유무에 따라 흡수되는 광 에너지의 관계를 나타낼 수 있는데, 이는 가스의 흡수계수와 밀접한 관계를 갖는다.
| (3) |
식 (3)에서 I는 적외선 센서에 도달하는 광 에너지, Io는 입사광 에너지, β는 가스 흡수 계수와 광 경로의 곱으로 정해지는 함수, x는 가스 농도를 의미한다.
따라서 광 경로 상에서 흡수되는 광 에너지는 식 (3)으로 표현할 수 있으며, 실제 가스 센서의 출력에서 살펴보면 식 (4)와 같고[9], Jun et al.[10]이 제시한 개념보다 더 정확하게 광 에너지 흡수에 따른 센서의 거동을 표현하고 있는 것으로 판단할 수 있다.
| (4) |
식 (4)로 정의된 광 흡수도, Fa에서 Vr은 기준 센서(reference sensor)의 출력전압, Vo는 이산화탄소 가스 센서의 출력전압, Z는 0 ppm에서 이산화탄소 가스 센서와 기준 센서의 전압 비를 의미한다. 식(4)에서 기준 센서의 전압이 가스 농도의 변화에 무관한 경우, 식 (5)와 같이 정리되므로, (3) 식에서 제시한 개념과 동일한 결과로 정리된다.
| (5) |
따라서 본 논문에서는 식 (5)로 광 흡수도를 정의하고, 온도에 따른 센서의 출력 보상과 농도 산출에 적용하였다.
2.2 센서의 제작 및 실험
본 연구 과정을 통해 제작된 비분산 적외선 가스센서의 사진을 제시하면 Fig. 1과 같다. 본 실험에 적용된 비분산 적외선 이산화탄소 가스 센서는 아날로그와 디지털 전원으로 분리되어 각 회로부에 인가되었고, 가스 센서들의 출력전압은 연산증폭기를 통해 1차 증폭되었다. 또한 이들 신호는 차동증폭기를 통해 2차 증폭되었으며, 각각의 증폭 신호들이 ADC (Analog-to-Digital converter)를 통해 센서의 출력전압으로 변환되었다. 디지털 신호로 변환된 출력 전압들은 MCU (microcontroller unit)에 저장된 프로그램을 통해 농도 산출에 응용되었고, 모든 신호들은 실험과정에서 센서의 특성을 종합적으로 판단하기 위해 DAC (Digital-to-Analog converter)와 RS485 통신 포트를 통해 외부의 컴퓨터에 연결되어 저장할 수 있게 하였다. 센서의 제작과 부품에 대한 정보는 이미 발표된 논문을 통하여 자세하게 확인할 수 있다[9].
Photo of fabricated NDIR CO2 gas sensor.
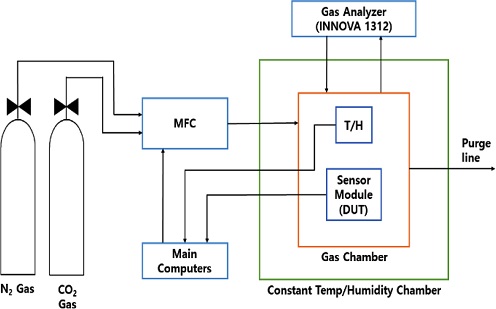
연구 개발된 센서 모듈에 대한 실험과 평가에 대한 기본적 사항은 기존 발표된 논문[9]에서 살필 수 있으며, 본 논문에서는 실험 과정에 대해서 제시하고자 한다. Fig. 2는 센서 모듈의 실험을 위한 장치의 개략도를 제시한 것이다.
Schematics of the experimental setup.
가스 챔버의 기준 상태(CO2 가스와 기타 가스가 없는 상태)를 확보하기 위해 고순도 질소가스를 약 10 분간 흘려줌으로써 챔버 내의 잔류가스를 제거하였다. 온도 변화에 따른 센서의 초기 출력전압을 확인하기 위해 항온·항습도 챔버에 센서 모듈을 넣고, 분위기 온도를 257 K, 267 K, 277 K, 300 K, 314 K, 324 K로 설정하여 0 ppm 상태에서의 출력전압을 확보하였다.
챔버 내부의 센서 모듈이 열적 평형 상태에 도달시키기 위해 온도 설정 후 7시간 이상 대기하였고, 온도 센서(Pt-100)의 출력 값이 이전 실험값의 ±0.3 oC 이내일 때, 각 센서에서 출력되는 값을 컴퓨터에 자동으로 저장시켰다. 또한 센서 모듈 내부의 잔류 가스를 고순도 질소 가스(99.99%)를 이용해 전부 배출시켜 내부의 이산화탄소 농도를 0 ppm에 가까운 상태로 만들어 준 후, 순차적으로 100, 200, 500, 1000, 1500, 3000, 5000 ppm의 가스를 400 초 동안 주입하여 온도와 이산화탄소 농도에 따른 센서의 출력을 확인하였다. 이때 압축 가스 상태에서 가스 챔버로 유입되는 가스의 온도 영향을 배제하기 위해 가스는 항온 항습조 내부의 약 3 m 길이의 배관을 거친 후, 가스 챔버에 유입되도록 챔버를 구성하였다.
한편 센서 모듈 내부의 가스 농도는 다중 가스 분석기 (INNOVA-1312)를 통해 ppm단위로 정확하게 측정함으로써 유입가스의 정확성을 확보하였다.
3. 결과 및 고찰
Fig. 3은 0 ppm 상태에서 온도의 변화에 따른 적외선 CO2 센서와 기준 센서의 출력전압을 나타낸 것이다.
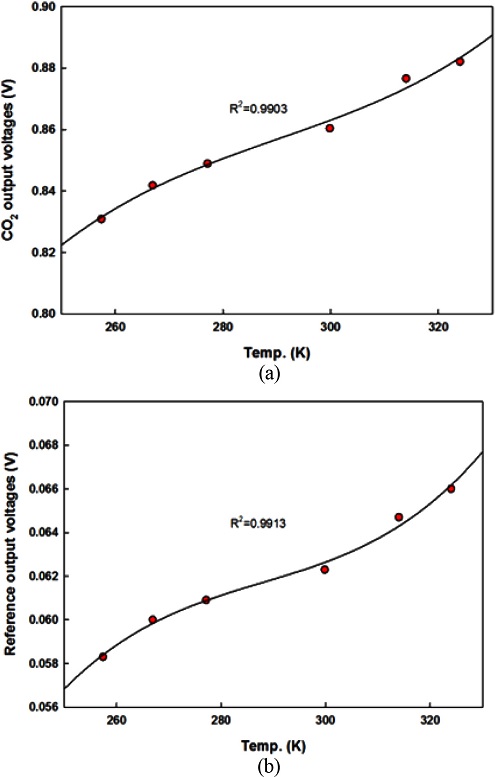
Initial output voltages of IR sensors as a function of temperatures: (a) CO2 sensor, (b) reference sensor [11].
이산화탄소 센서와 기준 적외선 센서의 초기 전압은 온도에 따른 3차 함수 형태로 분석되었으며, 온도가 증가함에 따라 기준 센서나 이산화탄소 센서 모두 출력 전압은 증가하는 것으로 나타났다. 이런 현상은 인가 전력이 일정할 때, 온도가 증가함에 따라 흑체인 적외선 광원의 표면온도가 증가하고, 이로 인한 입사 에너지 증가에 기인한다는 기존 연구결과와 잘 일치되는 것을 알 수 있다[11].
제작된 센서 모듈의 이산화탄소 가스 농도 의존성을 살펴본 결과를 제시하면 Fig. 4와 같다. Fig. 4(a)는 이산화탄소 센서와 기준 센서의 출력을 차동 증폭한 결과이고, Fig. 4(b)는 개별적으로 증폭된 출력 전압의 비를 구한 것이다. Fig. 4에 제시된 것과 같이 동일한 농도구간에서 출력전압의 변화폭이 차동 증폭된 결과보다 4 배 이상 큰 값을 갖고 있어, 신호처리 과정에서 분해능을 향상시킬 수 있을 것으로 판단된다. 따라서 본 연구에서는 증폭된 전압비를 농도 측정에 적용하고자 하였다.
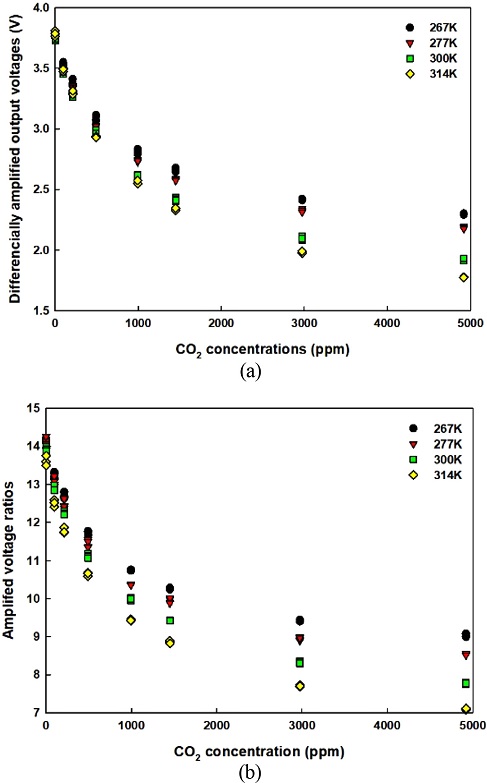
Amplified output voltages of infrared sensors as a function of CO gas concentrations: (a) differentially amplified output voltages, (b) voltage ratios.
측정 분위기 온도에서 적외선 센서에 조사되는 에너지를 식 (5)를 통해 광 흡수도를 살펴보고, 각각의 농도에서 광 흡수도의 기울기를 구하여 이를 정규화한 결과를 제시하면 Fig. 5와 같다.
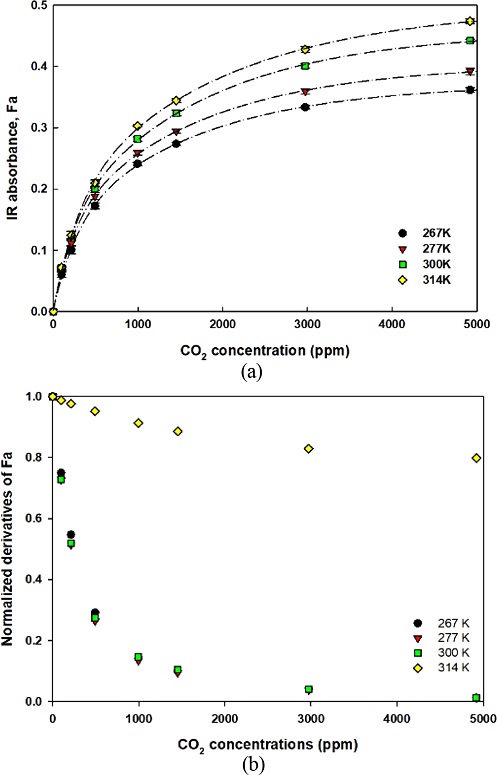
Absorbance of IR as a function of CO2 gas concentrations: (a) IR absorbance [11], (b) normalized derivatives of IR absorbance.
가스의 농도가 증가할수록, 또한 주변 온도가 상승함에 따라 광 흡수도는 증가하는 것을 Fig. 5(a)를 통해 알 수 있다. 따라서 광 흡수도가 온도의 함수로 정의됨을 본 연구결과를 통해 명확하게 확인할 수 있었으며, 이는 기존 연구결과와 부합됨을 알 수 있다[11,12].
한편 광 흡수도를 가스 농도 분석 알고리즘에 적용하기 위한 기준을 확보하고자 광 흡수도의 분위기 온도와 가스 농도와의 상관성을 살폈다. 광 흡수도를 각 온도와 농도에서 1차 미분한 후, 이들을 0 ppm에서의 값을 기준으로 정규화한 결과가 Fig. 5(b)이다. Fig. 5(b)에서 300 K 이하에서 정규화된 기울기는 모든 측정 온도에서 유사한 값을 갖고 있었으나, 314 K에서의 결과는 상이한 특징을 나타내고 있음을 볼 수 있다. 또한 정규화한 기울기는 가스 농도 500~1500 ppm에서 급격하게 변화되어 3000 ppm 이상의 가스농도에서 거의 0에 가까운 값을 갖게 됨을 볼 수 있었다.
따라서 본 연구에서는 500 ppm, 1000 ppm, 1500 ppm에서 광흡수도의 온도에 따른 함수를 구하고, 이들 농도를 기준으로 출력 특성을 구분한 후, 출력 전압을 통한 가스 농도 산출을 시도하였다. 가스 농도 1000 ppm (정규화한 광 흡수도의 미분값은0.14)을 기준으로 출력 특성을 구분하여 제시하면 Fig. 6과 같다.
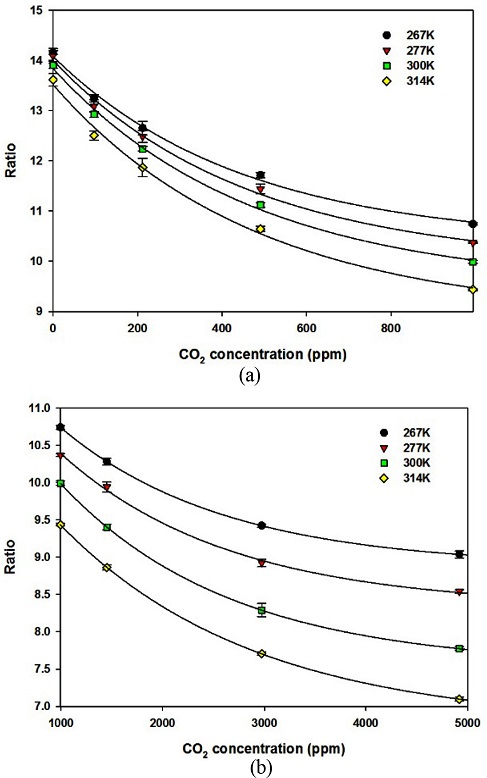
Partitioned amplified voltage ratios as a function of CO2 gas concentrations: (a) 0 to 1000 ppm, (b) 1000 to 5000 ppm.
Fig. 6은 식 (2)에서 제시한 수식이 아닌 세 개의 파라미터를 갖는 지수함수[8,9]로 출력전압을 추정한 곡선을 포함한 결과를 제시한 것으로, 측정된 전압을 정확하게 표현하고 있음을 확인 할 수 있었다. 따라서 광 흡수도를 구하고, 이를 통해 출력전압을 구간 분할하며, 세 개의 파라미터를 갖는 지수함수를 통해 추정농도를 구하는 관계식을 도출함으로써 식 (2)가 주는 어려움을 극복할 수 있을 것으로 판단할 수 있었다. 그러나 기준점을 결정하기 위해 기울기의 변화가 큰 세 점을 기준으로 추정 농도에 대한 오차를 살펴본 결과를 제시하면 Table 1과 같다.
Limits of errors according to the normalized derivatives of absorbance, Fa.
Table 1에 제시된 광 흡수도의 미분을 정규화한 값에 따라 오차의 하한 값과 상한 값은 정규화된 미분 값이 감소함에 따라 오차의 하한과 상한이 감소함을 알 수 있다. 또한 괄호 안에 제시된 차동 증폭된 출력을 통한 오차와 비교하였을 때, 출력 전압비를 통한 농도 추정의 오차가 상대적으로 큰 것을 알 수 있었다. 비록 Fig. 4에 표현된 바와 같이 전압비가 차동 증폭 값에 비해 큰 전압 변동을 나타내고, 이로 인해 분해능이 향상될 것으로 기대하였지만, 추정 농도 오차는 차동 증폭 값을 이용한 결과에 비해 증가하는 것으로 나타났다.
Fig. 6과 Table 1의 분석결과를 바탕으로 프로그램을 수정하여 MCU에 입력한 후, 임의 온도에서 측정된 전압과 전압 비를 통해 측정 농도를 도출한 결과를 나타내면 Fig. 7과 같다. 정규화된 광 흡수도의 미분 값이 0.10인 지점 (광 흡수도의 초기 기울기가 90%로 감소하는 지점)을 기준으로 가스 농도측정 알고리즘을 구분하는 프로그램을 실장하여 임의의 온도에서 가스 농도를 측정한 결과인 Fig. 7을 통해 전체 온도구간에서 최대 5% (3000 ppm에서) 미만의 측정오차를 나타내었다.
Measured CO2 concentrations vs. standard CO2 concentrations.
본 연구과정을 통해 둘 이상의 광 경로로 표현되는 출력 특성을 광 흡수도의 정의와 이의 기울기 변화의 정규화를 통해 표준 가스의 농도를 최대 5% 이내에서 정확하게 측정할 수 있는 알고리즘을 설정할 수 있었다. 또한 1차 증폭된 출력 전압의 비를 이용한 농도 측정은 분해능을 향상시킬 수 있었으나, 열잡음에 의한 영향을 배제할 수 없음으로 인해 농도 측정에서의 오차는 차동 증폭한 결과에 비해 취약한 특성을 갖고 있음을 비교 검토를 통해 확인할 수 있었다.
4. 결 론
본 논문에서는 두 개 이상의 광 경로와 이에 따른 지수 함수적 특성을 갖는 비분산 적외선 가스 센서의 농도 측정 알고리즘의 개선을 위해 광 흡수도를 정의하고, 이의 기준을 통해 농도 측정의 오차 분석을 진행하였다. 광 흡수도의 정의와 적용을 통해 광 흡수도의 미분 값을 정규화하고, 출력 특성을 구분함으로써, 두 개의 지수함수로 표현되는 출력 특성을 하나의 지수함수로 표현할 수 있었다. 또한 광 흡수도 변화의 기울기가 초기값의 90%로 감소하는 지점을 기준으로 출력 특성을 구분하고, 각 영역의 특성을 알고리즘으로 반영한 농도 산출법이 표준 가스 농도를 최대 5 % 이내에서 정확하게 측정함을 확인하였다. 따라서 광학적 구조물에 따른 출력 특성의 분석과 광 흡수도 정의를 통해 보다 정확하게 가스 농도를 측정하고, 온도 보상할 수 있음을 본 연구를 통해 알 수 있었다.
Acknowledgments
This research was supported by R&D center for Green Patrol Technologies through the R&D for Global Top Environmental Technologies funded by Ministry of Environment, Republic of Korea.
REFERENCES
- https://www.sensirion.com/kr/environmental-sensors/carbon-dioxide-sensors/carbon-dioxide-sensors-co2/, (retrieved Dec. 29, 2020).
- http://allsensing.com/product/list.html?cate_no=62/, (retrieved Dec. 29, 2020).
- J. S. Park and S. H. Yi, “Temperature compensation of NDIR CO gas sensor implemented with ASIC chip”, KIGAS, Vol. 11, No. 1, pp. 40-45, 2007.
-
S. H. Yi, “Temperature compensation methods of nondispersive infrared CO gas sensor with dual ellipsoidal optical waveguide”, Sensor Mater., Vol. 29, No.3, pp. 243-252, 2017.
[https://doi.org/10.18494/SAM.2017.1439]
-
S. H. Yi, Y.H. Park, and J. K. Lee, “Temperature dependency of nondispersive infrared carbon dioxide gas sensor by using White-cell structure”, J. Sens. Sci. Technol., Vol. 25, No. 5, pp. 377-381, 2016.
[https://doi.org/10.5369/JSST.2016.25.5.377]
-
T. A. Vincent and J. W. Gardner, “A low cost MEMS based NDIR system for the monitoring of carbon dioxide in breath analysis at ppm levels”, Sens. Actuators B-Chem,, Vol. 236, pp. 954-964, 2016.
[https://doi.org/10.1016/j.snb.2016.04.016]
-
S. H. Yi, “Temperature dependency of non-dispersive infrared carbon dioxide gas sensor by using infrared sensor for compensation”, J. Sens. Sci. Technol., Vol.25, No. 2, pp. 124-130, 2016.
[https://doi.org/10.5369/JSST.2016.25.2.124]
-
J. H. Kim and S. H. Yi, “Effects of temperature and humidity on NDIR CO2 gas sensor”, J. Sens. Sci. Technol., Vol. 26, No. 3, pp.179-185, 2017.
[https://doi.org/10.5369/JSST.2017.26.3.179]
-
S. H. Yi, “Infrared light absorbance: a new method for temperature compensation in nondispersive infrared CO2 gas sensor”, J. Sens. Sci. Technol., Vol 29, No. 3, pp. 303-311, 2020.
[https://doi.org/10.46670/JSST.2020.29.5.303]
-
L. Jun, T. Quilin, Z. Wendong, X. Chenyang, G. Tao, and X. Jinjun, “Miniature low power IR monitor for methane detection”, Measurement, Vol. 44, pp. 823-831, 2011.
[https://doi.org/10.1016/j.measurement.2011.01.021]
- H. G. Park and S. H. Yi, “Analysis of output voltage properties of non-dispersive infrared gas sensors according to ambient temperature”, J. Sens. Sci. Technol., Vol. 27, No.3, pp. 294-299, 2018.
-
W. B. De More and M. Patapoff, “Temperature and pressure dependence of CO extinction coefficient”, J. Geophys. Res., Vol. 77, No. 31, pp. 6291-6293, 1972.
[https://doi.org/10.1029/JA077i031p06291]