[ Article ]

JOURNAL OF SENSOR SCIENCE AND TECHNOLOGY - Vol. 32, No. 1, pp.62-65

ISSN: 1225-5475 (Print) 2093-7563 (Online)

Print publication date 31 Jan 2023

Received 23 Jan 2023 Accepted 31 Jan 2023

DOI: https://doi.org/10.46670/JSST.2023.32.1.62

거대 스케일 광학 센서 설계를 위한 파동 시뮬레이션(Wave Simulation) 기법 연구

이용훈¹ ; 권태윤² ; 최무한¹^{, +}

1경북대학교 전자공학부
2㈜한화방산

Wave Simulation Technique for Large-scale Optical Sensor Designs

Yong-Hoon Lee¹ ; Tae Yoon Kwon² ; Muhan Choi¹^{, +}

1School of Electronics Engineering, Kyungpook National University 80, Daehak-ro, Buk-gu, Daegu 41566, Republic of Korea
2Department of Navigation Systems, Hanwha Munitions Corporation 10, Yuseong-daero 1366beon-gil, Yuseong-gu, Daejeon 34101, Republic of Korea

Correspondence to: ⁺ mhchoi@ee.knu.ac.kr

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The wave mode calculation of a large-scale optical system in comparison to the working wavelength is practically impossible because the computational cost increases exponentially. In this paper, we propose a method that can obtain the optical mode in a large-scale optical system. The method carries out simulations by dividing the calculation area into blocks and moving along the light axis along which the light propagates. By applying this method to the calculation of resonant modes in a ring-type optical resonator, which is mainly used for ring laser optical gyro sensors, the efficiency of the proposed method was verified.

Keywords:

Finite difference time domain (FDTD) method, Gyro-sensor, Ring resonator, Resonant mode

1. 서 론

광공진기(optical resonator)를 포함하는 광자이로 센서(optical gyro-sensor) 혹은 반도체 레이저와 같은 광소자의 광모드(optical mode)를 분석하기 위해서는 주어진 경계조건에서 시간과 공간의 맥스웰 방정식을 풀어야 한다. 파동방정식을 수치해석적으로 푸는 방법으로는 FEM(Finite element method)[1] 혹은 FDTD(Finite difference time domain)[2,3] 방법에 기반하는 수치해석 프로그램이 폭넓게 사용되고 있다. 그러나, 이러한 방법들은 우리가 다루어야 할 시스템의 크기가 동작 파장에 비해 매우 클 경우, 계산 프로그램이 필요로 하는 컴퓨터 리소스와 계산량이 기하급수적으로 늘어나는 단점이 있다. 따라서, 파장 대비 거대 스케일의 광학시스템을 설계하는 경우는 대개 Ray 모델을 통해 근사적이거나 필요한 정보들만 획득하는 한정적인 시뮬레이션 방법을 사용한다[4].

본 연구에서는 계산 영역을 블록화하여 빛이 전파하는 광 축 근처에서 순차적으로 이동하며 시뮬레이션하는 방법을 사용하여 기존 시뮬레이션 방식으로는 불가능한 파장 대비 거대 스케일의 광학시스템의 광 모드를 파동광학적으로 구할 수 있는 방법론을 제시하고자 한다. 또한 본 방법론을 링레이저-광자이로 센서[5-7] 등에 주로 사용되는 링형(ring-type) 광공진기에 적용하여 그 해를 파동광학적으로 구함으로써 제시된 방법의 효율성을 검증하고자 한다. 개발된 방법론은 거대 광학시스템의 파동광학적 특성 분석에 유용하게 사용될 것으로 기대된다.

2. 연구 방법

2.1 기존 FDTD 방법을 사용하여 공진기 광모드 Profile을 구할 때 소요되는 컴퓨팅 리소스 소요에 대한 고찰

전통적으로 4개의 3차원 거울로 구성된 링형 광공진기의 광모드를 파동광학적으로 계산하여 그 field 분포 및 모드의 Q값 등을 구하고자 할 경우에 주로 FDTD 방법이 사용된다. 이러한 방법은 공진모드에 관련된 모든 field 분포, 모드 진동수, 모드 Q 값 등을 한번의 시뮬레이션으로 이끌어 낼 수 있는 장점이다. 그러나, 계산 가능한 시스템의 크기가 컴퓨터 리소스에 의해 크게 제한되어 산업적으로 요구되는 실측 크기의 시스템에 대한 계산은 불가능하여 현실적으로 토이 모델(Toy model)계산을 통해 한정된 크기의 시스템에 대해서만 모드 계산이 가능하다.

Fig. 1.

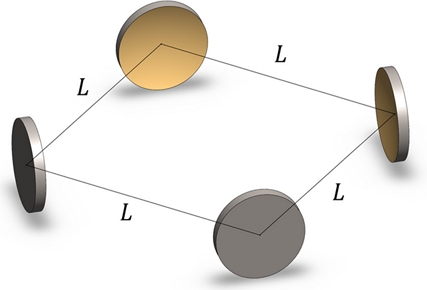
An optical ring resonator system for optical gyro-sensor application (radius of curvature of mirrors: 22.47 μm).

Fig. 2.

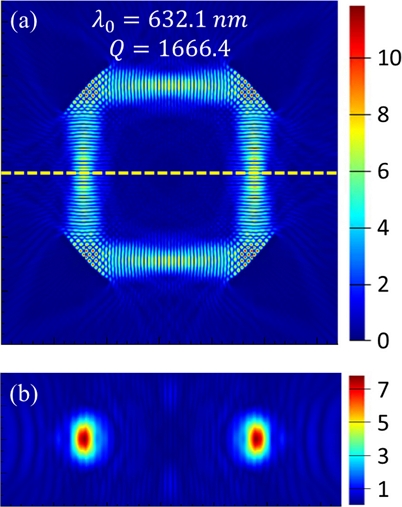
An optical mode calculated from commercial FDTD solver. (a) top view, (b) cross-sectional view at yellow dashed-line in the Fig. 2(a).

실제로 FDTD 방법의 경우 시뮬레이션하고자 하는 시스템의 크기가 커지면 계산에 필요한 메모리는 시스템 사이즈 길이 스케일(길이 L)의 대략 3제곱으로 비례하며, 계산 시간은 4제곱에 비례한다고 알려져 있다. Table 1에는 광파장 영역에서 시스템 사이즈 증가에 따라 요구되는 메모리 요구량을 표시하였다. 더욱 더 심각한 문제는 컴퓨터의 하드웨어 요구량의 증가에 따른 시뮬레이션 소요시간은 더욱더 가파르게 증가한다는 데 있다. 따라서, 예시로 제시한 링형 광공진기의 경우 실제로 200 μm×200 μm×200 μm 크기 이상 시스템을 연구실 수준에서 Full wave 수치계산한다는 것은 현실적으로 불가능하다고 할 수 있다.

Table 1.

System size vs. required memory size for conventional FDTD simulations.

Fig. 3.

Schematic of the concept of the proposed method.

2.2 계산 영역 블록화를 통한 실측 크기의 광학 시스템 파동시뮬레이션 방법론

본 연구에서는 한정된 리소스를 활용하여 실측 크기에 근접하는 광공진모드를 계산할 수 있는 새로운 EM(electromagnetic) 시뮬레이션 방법론을 제시하고 이를 코드화하여 거대스케일의 광학시스템에 적용하고자 한다. 제시하는 방법의 핵심 아이디어는 계산하고자 하는 광학시스템(예시로 링레이저 광공진기) 전체 영역을 하나의 도메인으로 계산하는 것이 아니라 여러 개의 계산블록으로 모듈화하고 파의 전파(propagation)에 따라 모듈을 직렬 배치하여 순차적으로 계산하는 것이다. 매번 블록 끝단에서 도출된 계산 결과를 다음 모듈의 입력값으로 피드백하여 계산을 진행한다.

제시하는 방법은 매 순간 한 블록에 해당하는 크기의 메모리와 계산영역을 가지므로 계산하는 컴퓨터의 리소스에 부담을 주지 않으며, 필요없는 영역에서는 계산을 수행하지 않으므로 매우 빠른 계산이 가능하다. 그러므로 계산 노드 (요소 Mesh 포인트)가 공진기 길이에 선형적으로 비례함에 따라 계산시간 및 메모리 소요량을 획기적으로 줄일 수 있다.

Table 2.

Simulation running time vs. system size for our proposed method

예시로서, Fig. 1에서 제시된 4개의 고반사율 거울로 이루어진 링형 광공진기의 광모드를 계산하는 알고리즘이 동작하는 순서는 다음과 같다.

1) 전체 시스템을 작은 영역으로 분할한다. 예를 들어 200 μm×200 μm×40 μm시스템의 경우 40 μm× 40 μm×40 μm 크기로 총 16개의 영역으로 분할한다. (25개 영역이 필요한 것처럼 보이지만, 중앙부에서 9개 영역은 계산에 필요 없으므로 16개 영역만 필요)

2) 초기 시작할 영역의 입력단에서 평면파를 전파시키고 출력단에서 전파된 빛의 정보를 주파수 영역(frequency-domain)에서 저장한다. 이때 출력단의 위치는 다음 번 시뮬레이션 입력단의 위치와 같다.

3) 시뮬레이션 영역을 변경하고 출력단에서 저장된 빛의 정보를 입력단에서 전파시켜 시간 영역(time-domain)에서 시뮬레이션을 수행한다.

4) 출력단에서 전파된 빛의 정보를 저장한다.

5) 3)~4)를 반복 수행한다.

3. 결과 및 고찰

기존 시뮬레이션의 경우, 한 변의 길이가 40 μm 정도의 작은 공진기 시뮬레이션에도 10 GB의 이상의 메모리가 요구되고, 실측 크기(수 cm)의 공진기의 경우 아예 파동 시뮬레이션은 불가능하다. 그러나, 본 연구에서 개발된 알고리즘은 실제 시스템의 크기가 아닌 계산 블록 모듈의 크기만큼의 물리적 메모리 크기가 요구되므로 원리적으로 공진기 크기에 구애받지 않고 계산을 수행할 수 있다. 실제 계산에 요구되는 컴퓨팅 리소스가 대략적으로 공진기 전체 길이에 단지 선형적으로 비례함을 알 수 있는데, 이로서 수 cm에 가까운 거대 스케일의 링형 광공진기의 모드 계산을 일반 PC 수준에서 수일 이내에 계산 가능하다.

Fig. 4.

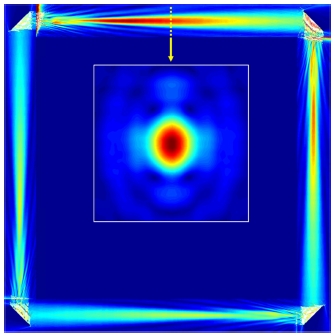
Top view and cross sectional view (at yellow dashed-line) of an optical mode obtained from the proposed method.

Fig. 5(a)는 반복 횟수에 따른 광공진기 모드의 패턴 변화를 보여준다. 반복 수행 횟수를 증가 시킬수록 광공진기의 모드 패턴이 기존 방법으로 구한 모드에 근접해감을 확인 할 수 있다. 광공진기 모드의 중요한 특성인자인 모드의 Q 값은 시간영역(Time domain)에서 field intensity I 와 Q 값의 관계인 아래 수식으로부터 구할 수 있다.

I = I 0 e - 2 t / τ, τ = 2 Q / ω N

(1)

Fig. 5.

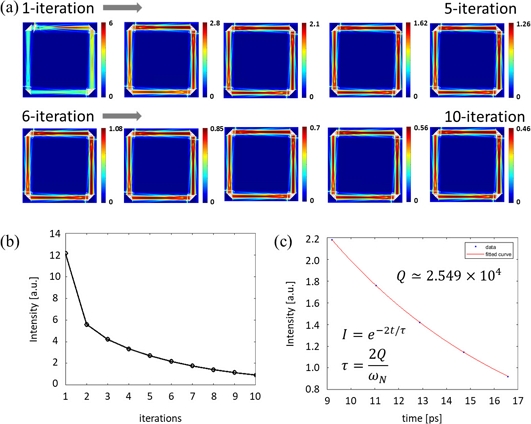
(a) Convergence of mode pattern in optical resonator with respect to increase of iteration number. (b) Maximum field intensity vs. iteration number. (c) Curve fit of maximum field intensity using Eq. (1).

여기서 I₀, T, Q, ω_N는 각각 초기 intensity, 시간, Q 값, 공진 각주파수이다

Fig. 5(b)는 각 반복에서 구한 모드의 중앙 지점에서 intensity를 추출하여 반복에 따라 intensity의 감쇠 정도를 보여준다. 이로부터 초기값을 배제하고 가공하여 Fig. 5(c)를 도출하였다. 곡선 피팅을 통해 추정한 모드의 Q 값은 230 μm×230 μm×25 μm 크기의 공진기에서 ~2.55×10⁴ 이다.

4. 결 론

동작 파장과 비교하여 매우 큰 스케일의 광학 시스템의 파동 모드 계산은 계산 자원과 소요 시간이 기하급수적으로 증가하기 때문에 실질적으로 불가능하다. 본 연구에서는 계산 영역을 블록으로 나누고 빛이 전파되는 광축을 따라 이동하면서 시뮬레이션하는 방식을 사용하여, 거대 스케일의 광학계에서 광모드를 파동광학적 계산으로 얻을 수 있는 방법을 제안하였다. 또한, 링 레이저 광자이로 센서 등에 주로 사용되는 링형 광공진기의 공진 모드 계산에 이 방법을 적용하여 제안한 방법의 효율성을 검증하였다. 비록 제시된 방법이 모든 광학시스템에 적용될 수는 없을 지라도 전자기장이 주로 축 주변으로 전파하는 광학시스템의 경우에 매우 강력한 수치계산 도구로 활용될 수 있을 것으로 기대된다.

Acknowledgments

이 논문은 2020학년도 경북대학교 연구년 교수 연구비에 의하여 연구되었음. (This research was supported by Kyungpook National University Research Fund, 2020)

REFERENCES

J. Jin, The Finite Element Method in Electromagnetics, IEEE Press, United States, pp. 223-267, 1993.
D. M. Sullivan, Electromagnetic simulation using the FDTD method, IEEE Press, United States, pp. 99-111, 2000. [https://doi.org/10.1109/9780470544518]
A. Taflove, S. C. Hagness, and M. Piket-May, Computational Electromagnetics: The Finite-Difference Time-Domain Method, Artech House, Boston, pp. 629-669, 2005. [https://doi.org/10.1016/B978-012170960-0/50046-3]
M. L. Stitch and M. Bass, Laser handbook Vol. 4, Elsevier, Netherlands, pp. 229-332, 1985.
H. R. Bilger, G. E. Stedman, and P. V. Wells, “Geometrical dependence of polarization in near-planar ring lasers”, Opt. Commun., Vol. 80, No. 2, pp. 133-137, 1990. [https://doi.org/10.1016/0030-4018(90)90374-3]
M. Faucheux, D. Fayoux, and J. J. Roland. “The ring laser gyro” J. Opt., Vol. 19, No. 3, p. 101, 1988. [https://doi.org/10.1088/0150-536X/19/3/001]
V. M. N. Passaro, A. Cuccovillo, L. Vaiani, M. De Carlo,and C. E. Campanella, “Gyroscope Technology and Applications: A Review in the Industrial Perspective”, Sensors, Vol. 17, No. 10, pp. 2284(1)-2284(22), 2017. [https://doi.org/10.3390/s17102284]