SOI 슬롯 광 도파로를 활용한 2×2 Balanced-Bridge Mach-Zehnder 간섭형 집적광학 바이오케미컬 센서 설계 및 성능평가
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
An integrated-optical biochemical sensor structure that can perform homogeneous and surface sensing using a 2×2 balanced-bridge Mach-Zehnder interference structure based on the optimized SOI slot optical waveguide was described, and its performance and characteristics were evaluated. Equations for the two output optical powers were derived and examined using the transfer matrices of a 3-dB coupler and phase shifter (channel waveguide). The length of the 3-dB coupler was determined such that the two output optical powers were same using these formulas. In homogeneous sensing, the effect of the refractive index of an analyte in the range of 1.33−1.36 on the two output optical power distributions was numerically derived, and the sensitivity was calculated based on each output and the difference between the two outputs, the former and the latter being 7.5796−19.0305 [au/RIU] and 15.2601−38.1351 [au/RIU], respectively. In the case of surface sensing, the sensitivity range of the refractive index of 1.337 based on each of the two outputs was calculated as -2.2490−-3.5854 [au/RIU] and 1.2194−3.8012 [au/RIU], and the sensitivity range of 4.8048−7.0694 [au/RIU] was confirmed based on the difference between the two outputs.
Keywords:
2×2 balanced-bridge Mach-Zehnder interferometer, Silicon on insulator(SOI), Slot optical waveguide, Integrated optical biochemical sensor, Homogeneous sensing, Surface sensing1. 서 론
지난 20여년동안 집적광학 바이오·케미컬 센서는 생화학, 의학 및 환경 분석 분야에서 바이오·케미컬 물질들을 감지하기 위한 뛰어난 도구로 평가되어 많은 연구가 진행되어왔다. 집적광학 센서는 광파의 강도, 파장, 위상 및 편광 등과 같은 다양한 물리적 파라미터들을 변환매개로 활용해서 다양한 분석물질(analyte)들에 대한 감지가 가능하며, 원격 및 다중 감지, 전자파 간섭에 대한 내성 등과 같은 고유한 특징들과 더불어 상대적으로 높은 감도(sensitivity), 매우 작은 footprint 및 대량 생산 능력 등과 같은 많은 장점들을 보유하고 있다. 더군다나 잘 개발된 다양한 수동 및 능동 광 집적 부품들과 관련된 기술들을 활용할 경우 매우 효율적이고, 가격 경쟁력을 갖춘 센서시스템을 구현할 수 있다[1-3].
평면(planar) 광 도파로에 기반한 집적광학 센서는 벌크(bulk) 광학장치 및 광섬유 기반 센서들에 비해서 다음과 같은 장점들을 가지고 있다. 평면 광 도파로는 표준 포토-리소그래피(photo-lithography) 기술을 사용하기 때문에 제조가 용이하여 저비용, 대량생산이 가능하고, 여러 분석 물질을 동시에 감지가 가능하도록 단일 기판에 여러 광 도파로 기반 감지 센서들을 집적화를 할 수 있다. 매우 잘 확립된 마이크로 일렉트로닉스 CMOS 공정프로세스를 활용할 수 있으며, 궁극적으로는 센서들을 동일한 CMOS 칩의 전자모듈들과 통합해서 센서를 칩-레벨 수준으로 집적화가 가능하다[4, 5].
실리콘계열 집적광학 바이오센서들은 Si/SiO2또는 Si3N4/SiO2 기반의 고 굴절 대비(high index contrast) 물질체계들로 구현된릿지(ridge) 또는 립(rib) 광 도파로 들을 이용해서 마하젠더 간섭기, 두-모드 또는 멀티모드 간섭기, 링 공진기, 브래그 격자 등과 같은 다양한 구조들로 구현하여 왔다[6,7]. 이렇게 제작된 광도파로들은 저 굴절률 물질 (즉 클래딩)로 둘러싸인 고 굴절률 물질 (코어)의 내부 전반사(TIR, total internal reflection)에 의해서 코어에 광파 대부분을 강하게 가두고 있지만 클래딩 영역에도 미약하지만 광파 일부가 존재하는데, 이것을 소산파 (evanescent wave)라 일컫는다. 따라서 이러한 소산파가 존재하는 클래딩 영역을 생체 분석물질로 대체할 경우, 소산파를 통해서 기본 도파모드의 유효굴절률과 위상에 영향이 미치게 되고, 이로부터 광파의 세기 또는 파장 등을 모니터링 해서 분석물질의 종류, 양(dose) 등을 감지하게 된다. 그러나 소산파 자체가 미약하기 때문에 근본적으로 큰 감도를 기대하기는 어렵다.
한편 2004년 Almeida 등이 슬롯(slot) 광 도파로 구조를 제안된 이후 이를 바이오·케미컬 센서에 활용하려는 연구가 오래 동안 진행되어왔다[8]. 슬롯 광 도파로의 경우 기본 모드의 많은 필드(field)분포가 두 개의 고 굴절률 레일 사이에 존재하고, 저굴절률 슬롯 영역을 통해서 전파된다. 즉 정량적인 관점에서 레일과 슬롯 경계 면에서 전기장의 불연속성으로 인해 모드필드의 상당 부분이 슬롯에 존재하게 된다. 따라서 슬롯에 레일보다굴절률이 작은 생체 분석물질로 채워질 경우 슬롯을 통해서 전파되는 기본모드와 더 강한 상호작용이 일어나서 우수한 감도특성을 기대할 수 있다[9-11]. 슬롯 광 도파로는 수직-슬롯 [12] 및 수평-슬롯 광 도파로 [13] 구조로 각각 구분되며, 수직, 수평 슬롯 광 도파로의 변형된 구조로 릿지-슬롯 [14]과 부하(loaded)-슬롯 [15]으로 구분된다. 바이오·케미컬 센서 구조로는 수직-슬롯과 릿지-슬롯 광 도파로 두 구조가 적합하며, 수직 슬롯 광 도파로 기반의 바이오·케미컬 센서 중심으로 전산해석을 포함해서 많은 연구가 진행되었다[16, 17].
광파를 기반으로 하는 집적광학 바이오·케미컬 센서는 라벨(label) 기반 감지와 라벨이 없는 (label-free) 감지방식으로 크게 구분된다. 전자 경우에는 형광 또는 광 흡수 마커(maker)를 통해서 표적 분자 또는 생체인식 분자를 감지해서 특정 샘플 분자의 존재를 정량화된 수치로 측정이 가능하나, 복잡한 액체 취급 및 라벨 공정, 상대적으로 긴 분석 시간과 부피가 큰 측정장치 그리고 숙련된 전문가가 필요하다. 한편 라벨이 없는 감지방식에서는 표적분자의 굴절률을 실시간으로 모니터링 할 수 있기 때문에 현장에서 활용할 수 있는 바이오·케미컬 센서로 매우 매력적으로 인식되어 집중적으로 많은 연구가 진행되었다[18, 19].
균일 센싱 이나 표면 센싱 원리는 소산파 기반 유효 굴절률 변화에 기인된 위상변화를 이용하고 있지만 정확한 위상변화 측정을 통해서 분석물질의 종류와 양을 파악하는 것이 쉽지 않기 때문에 위상변화를 보다 측정이 용이한 세기변화로 전환시켜 측정하는 것이 바람직하며, 이러한 물리적 매개 변환은 마하젠더-간섭기 [20], 두-모드 [7] 또는 다중모드 결합기 [21], 링-공진기 [22]등을 통해서 구현되었다. SOI 또는 Si3N4 립 또는 릿지 광도파로들을 앞서 언급된 구조들에 적용해서 다양한 광 집적 센서들을 제작하였고, 많은 연구들이 진행되었다. 그러나 슬롯 광도파로 구조 최적화에 대한 연구는 진행되었지만, 이를 활용해서 세기 기반의 센서에 대한 연구는 다양하게 수행되지 않은 것으로 파악되고 있다. 따라서 본 연구에서는 최적화된 슬롯 광도파로를 2×2 Balanced-Bridge Mach-Zehnder 간섭 구조 [23, 24]에 적용하고, 균일 및 표면 센싱을 통해서 출력 광 파워에 미치는 영향과 이에 대한 감도를 수치해석을 통해서 체계적으로 분석하였다. 2장에서는 분석물질의 굴절률과 두께에 따른 수직-슬롯 광 도파로의 최적화된 제원에 대해서 연구된 참고문헌의 연구결과들을 검토해서, 슬롯의 제원을 결정하였다[25]. 3장에서는 2×2 Balanced-Bridge Mach-Zehnder 간섭기 구조에 대한 수식과 설계 절차를 제시하였고, 이 구조를 기반으로 균일 센싱과 표면 센싱에 적합한 센싱영역 구조를 제시하고, 출력 광 파워분포와 감지 성능을 Photon Design의 FIMMWAVE, FIMMPROP들을 이용해서 전산해석을 수행하였으며 [26], 결과들을 4장에 제시하였고, 5장에서 결론으로 마무리 하였다.
2. 수직-슬롯 광 도파로의 모드 해석
Maxwell 파동방정식 기반으로 슬롯 광 도파로에 대한 광파해석에 대한 연구는 많이 이루어졌으며, 자세한 수식 전개 과정은 여러 참고문헌 [27, 28]에서 확인 가능하기 때문에 본 장에서는 균일 및 표면 센싱 구조로부터 도출된 결과들로부터 최적화된 제원을 도출하였다.
2.1. 광 도파로 감도
감도(sensitivity), 검출한계(limit of detection), 선택성(selectivity), 재현성(reproducibility), 안정성(stability) 및 분해능(resolution)과 같은 다양한 성능 지수들을 센서 성능을 평가하는데 사용되지만, 이들 중에서도 감도를 센서 성능평가에 가장 비중 있는 지표로 활용되고 있다. 광도파로 기반 집적광학 센서 감도는 광도파로 감도 (waveguide sensitivity, Sw)와 아키텍처 감도(architecture sensitivity, Sa)로 구성되며, 전자는 분석물질의 굴절률 또는 클래딩 박막 두께 변화를 통해서 도파모드의 유효 굴절률에 반영된다. 그러나 광도파로 모드의 유효 굴절률은 직접 측정하기가 수월하지 않은 물리적 지수이므로, 이를 유용하게 활용하려면 쉽게 감지할 수 있는 물리적 양으로 변환시키는 것이 필요하며, 이러한 변환은 다양한 광-집적 아키텍처들을 활용해서 달성될 수 있다. 이러한 아키텍처는 Mach-Zehnder 간섭계 [20], Young 간섭계 및 다중 모드 간섭계 [21]와 같은 간섭 구조와 링 공진기(resonator) [9] 및 Fabry-Perot 공진기와 같은 공진구조 두 카테고리로 분류할 수 있다. 간섭 아키텍처에서 굴절률 변화는 위상 변화(∆φ)로 전환되는 반면, 공진 아키텍처에서는 공진 파장의 변화(∆λ) 로 나타나게 된다. 먼저 간섭 구조에 대한 감도는 다음과 같다. Swh는 균일센싱에서 광도파로 감도를 의미한다.
| (1) |
여기서 λo은 입사 광파의 파장, L은 센싱 영역의 길이, na는 분석물질의 굴절률이다. 한편 공진 구조에 대한 감도는 다음과 같이 정의된다. Sws는 표면센싱에서 광도파로 감도를 의미한다.
| (2) |
여기서 λr은 공진 파장, ng는 도파로의 그룹 굴절률(group refractive index), ta는 분석물질의 두께이다.
2.2. 균일 센싱의 광 도파로 감도
Fig. 1(a)의 슬롯 광 도파로 구조에 기반해서 균일 센싱을 검토하였다. 분석물질의 굴절률이 TE 기본 모드의 유효 굴절률에 미치는 영향을 슬롯 폭 80 nm, 120 nm, 160 nm 각각에 대한 전산해석을 수행해서 Fig. 1(b)와 같은 결과를 얻었으며, 이 결과에 식 (1)을 적용해서 Fig. 1(c)와 같이 광 도파로 감도를 계산하였다. 특히 4 종류의 분석물질 즉 Water (1.31), Isopropanol (1.377), Ethylene-Glycol (1.505), Sodium-Chloride (1.5443)들이 유효굴절률에 미치는 영향을 강조하기 위해서 Fig. 1(b)에 표시하였다. 분석물질 굴절률, 1.3−1.55 범위에서 슬롯 폭에 따른 감도 특성들을 비교해보면 120 nm 슬롯 폭이 편차가 매우 작은 감도 특성을 보여주고 있다.
2.3. 표면 센싱의 광 도파로 감도
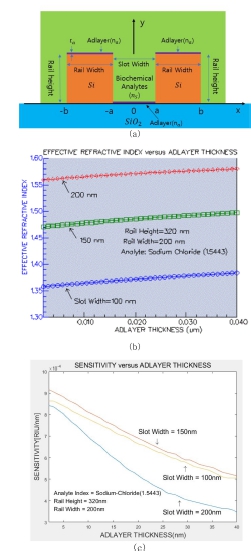
Fig. 2(a)의 슬롯 광 도파로 구조에 기반해서 표면 센싱을 검토하였다. 분석물질의 두께가 TM 기본 모드의 유효 굴절률에 미치는 영향을 슬롯 폭 100 nm, 150 nm, 200 nm 각각에 대한 전산해석을 수행해서 Fig. 2(b)와 같은 결과를 얻었으며, 이 결과에 식 (1)을 적용해서 Fig. 2(c)와 같이 광 도파로 감도를 도출하였다. 분석물질의 두께 1−40 nm 범위에서 슬롯 폭에 따른 감도를 계산하였으며, 균일 센싱과 비교해서 감도는 약 10-4 수준으로 매우 작았으며, 따라서 상대적으로 그래프 상에서 감도편차가 큰 것으로 나타났다.
3. 2ⅹ2 Balanced Bridge 마하젠더 간섭기의 동작원리
Fig. 1(a), Fig. 2(a)와 같이 균일 및 표면 센싱으로 부터 감지된 유효굴절률 변화로부터 광파는 위상변화를 겪게 되고, 이를 세기(intensity) 변화로 전환되도록, Fig. 3과 같은 2ⅹ2 Balanced-Bridge 마하젠더 간섭기를 변환소자로 채택하였다. 이 구조는 입·출력 포트 앞 뒤로 각각 두 개의 3-dB 방향성 결합기, 두 결합기 사이에 동일한 채널 광 도파로 들을 연결해서 구성된다. 두 입력 포트 중 어느 하나에 광 파워를 입사시키면 두 출력 광 파워가 동일하게 되도록 두 방향성 결합기 길이 Lc1, Lc2를 결정하는 것이 필요하며, 다음과 같이 방향성 결합기의 전달 매트릭스를 이용해서 설계방법을 제시하였다[23, 24].

Schematic diagram of 2×2 balanced-bridge Mach-Zehnder Interferometer utilizing vertical SOI slot waveguide.
방향성 결합기를 구성하는 두 슬롯 광 도파로가 동일할 경우,두 광 도파로의 전파상수, β=β1=β2와 결합계수 (couplingcoefficient), κ=κ1=κ2는 동일하며, 그리고 손실이 없다고 가정할 경우, 3-dB 결합기 전달 매트릭스는 다음과 같이 나타낼 수 있다.
| (3) |
Fig. 3 구조의 두 채널 광 도파로 중 하나에 형성된 센싱 구조로부터 추가적인 위상변화, Δθ를 포함할 경우, 소자 전체 전달 매트릭스는 다음과 같이 나타낼 수 있다.
| (4) |
위 식에서 동일한 두 결합기를 활용하는 것으로 가정해서, 각 결합길이, LC로 표기하였다. 따라서 입력광파 Ei2=0 설정하고, 두 출력 광 파워는 아래와 같이 유도된다.
| (5-1) |
| (5-2) |
예상한대로 두 출력 광 파워의 합은 P01+P02임을 식 (5)를 통해서 확인될 수 있으며, 제안된 소자가 선형(linearity)을 유지하면서 최대 감도 성능을 보장하기 위해서 두 출력 광 파워가 동일하게 유지해야 된다. 따라서 Δθ=0, P01=P02 조건하에서 3-dB 결합길이는 다음과 같은 조건을 만족해야 된다.
| (6) |
κLC를 변화시키면서 식 (5)의 두 출력 광 파워의 전송특성은 Fig. 4와 같이 도출되었으며, 동일한 두 출력 광 파워를 유지되도록 식 (6)으로부터 3-dB 결합기 길이를 결정할 경우 굴절률 변화에 따른 민감한 감도 특성을 기대할 수 있다. LC = 140.61 μm, L=10,000로 설정하고, FIMMPROP를 활용해서 Fig. 5와 같이 출력 광 파워가 동일하게 양분되는 광파전송 특성을 확인할 수 있다

Transfer curve with various values of κLC. The balanced MZI structure show square sinusoidal transfer function showing very steep slope at half power.
4. 균일 및 표면 감도
2×2 Balanced-Bridge 마하젠더 간섭기의 채널 광도파로 센싱 영역에 균일 및 표면 센싱 기능을 수행할 수 있도록 Fig. 6과 같은 두 구조로 변형이 가능하다. 분석물질의 굴절률이 슬롯에 집중적으로 분포되어 있는 TE (균일센싱) 또는 TM (표면센싱) 도파모드의 유효굴절률에 미치는 정도에 따라 두 출력 광파의 세기가 달라지게 되며, 이를 모니터링 해서 센싱 감도를 평가할 수 있다.

Detailed schematic layout and dimensions of 2×2 Balanced-Bridge Mach-Zehnder Interferometer for (a) homogeneous and (b) surface sensing. (slot width=120 nm, rail width=200 nm, rail height=320 nm).
4.1. 균일 센싱 감도
균일 센싱이 수행되도록 센싱 영역을 Fig. 6(a)로 수정하고, 분석물질 굴절률 1.33−1.36 범위에서 FIMMPROP 전산해석으로 두 출력 광 파워에 대해서 Fig. 7(a)와 같은 결과를 얻었다. 이 경우에 reference 채널 및 센싱 영역의 길이를 각각 10,000 μm, 20 μm, 그리고 3-dB 결합기 길이는 138.48 μm로 설정하였다. 예상한대로 두 출력 광 파워 중에서 Po1은 감소하고, Po2는 증가됨을 확인할 수 있으며, 굴절률이 1.36에 근접하면서 출력파워가 포화되기 시작하고, 미세한 비선형 특성을 나타내고 있다. 이어서 분석물질 굴절률 변화에 따른 출력 광 파워의 변화로 감도를 정의하고, 다음과 같은 수식으로 나타낼 수 있다.

The Numerical results of (a) normalized two output power: p1(below) and P2(above), (b) sensitivity based on each output, (c) sensitivity based on the output power difference versus analyte refractive index, and (d) evaluated sensitivity range.
| (7) |
따라서 이 구조에서는 두 출력 광 파워를 각각 모니터링 하거나 또는 두 출력 광 파워의 차(difference)를 모니터링 해서 센서로 활용할 수 있는 구조적인 장점이 있다. 두 출력 광 파워각각에 대한 감도는 Fig. 7(b)와 같으며, 측정 굴절률 범위에서 감도가 증가 또는 감소됨을 알 수 있으며, 감도의 편차는 약 5 dB 정도이다. 한편 Fig. 7(c)와 같이 두 출력 차를 적용할 경우 감도 자체는 전자보다는 훨씬 크지만, 굴절률 간에 편차도 확대됨을 확인할 수 있었으며, 각각에 대한 감도의 범위를 Fig. 7(d)에 요약하였다.
4.2. 표면 센싱 감도
표면 센싱이 수행되도록 센싱 영역을 Fig. 6(b) 구조로 수정하고, 분석물질의 두께 1−20 nm 범위에 대한 두 출력 광 파워의 전산해석으로 Fig. 8과 같은 결과를 얻었다. Fig. 8(a)는 기준(reference) 채널 및 센싱 영역의 길이 각각을 10,000 μm,100 μm, 그리고 3-dB 결합기 길이는 141.16 μm로 설정하고, 분석물질의 굴절률을 1.336, 1.505, 1.5443으로 가정해서 전산해석을 수행하였다. 이 경우에도 균일 센싱과 유사하게 분석물질의 두께가 증가함에 따라 두 출력 광 파워 중에서 P1은 감소하고, P2는 증가됨을 Fig. 8(a)와 같이 확인할 수 있었으며, 분석물질의 두께가 두꺼워질수록 미세한 비선형 특성을 나타내고 있다. 한편 Fig. 8(b)는 분석물질의 굴절률을 1.337로 고정하고, 센싱 영역의 길이 100, 200, 300 μm 각각에 대해서 분석물질의 두께가 출력 광 파워에 미치는 영향을 해석한 결과를 보여주고 있다. 센싱 영역의 길이가 길수록 비선형 특성이 나타남을 확인할 수 있으며, 가급적 센싱 영역 길이가 짧을수록 우수한 선형 특성을 관찰할 수 있다. 이 경우에 분석물질두께 변화에 따른 출력 광 파워의 변화로 표면 센싱의 감도를 다음과 같이 정의할 수 있다.
| (8) |

The Numerical results of normalized two output power versus adlayer thickness (a) for specific analyte refractive index and (b) for sensing area length.
이 구조에서도 두 출력 광 파워를 각각 모니터링 하거나 또는 두 출력 광 파워의 차(difference)를 모니터링 해서 센서로 활용할 수 있다. Fig. 8(a)에 대한 두 출력 광 파워 각각에 대한 센싱 감도는 앞서 언급된 분석물질 굴절률 각각에 대해서 Fig. 9(a)와 같은 결과를 얻었다. 분석물질 두께가 증가함에 따라 감도는 증가 또는 감소됨을 보여주고 있으며, 감도의 편차는 굴절률에 따라 큰 차이를 보이고 있다. 한편 Fig. 9(b)와 같이 두 출력 차를 활용할 경우 감도 자체는 전자보다는 훨씬 크지만, 굴절률간에 편차도 확대됨을 확인할 수 있었으며, 각각에 대한 감도의 범위를 Fig. 9(c)에 요약하였다.
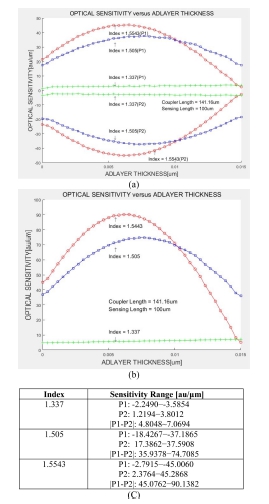
The Numerical results of sensitivity based on (a) each output, (b) output power difference versus adlayer thickness for specific analyte refractive index, and (c) the summary of sensitivity range.
Fig. 10은 Fig. 8(b) 대해서 분석물질 두께에 따른 감도를 두 출력 차를 이용해서 전산 해석한 결과들이다. Fig. 10(a) 두 출력 광 파워 각각에 대해서, Fig. 10(b)는 두 출력 광 파워 차에 대한 감도이다. 이 경우에도 Fig. 9와 같이 전자는 분석물질 두께가 증가함에 따라 감도가 증가 또는 감소됨을 보여주고 있으며, 감도의 편차는 굴절률에 따라 큰 차이를 보이고 있다. 한편 후자는 두 출력 차를 활용한 경우이며, 감도 자체는 전자보다는 훨씬 크지만, 굴절률 간에 편차도 확대됨을 확인할 수 있었으며, 각각에 대한 감도의 범위를 Fig. 10(c)에 요약하였다.

The Numerical results of sensitivity based on (a) each output, (b) output power difference versus adlayer thickness for sensing area length and (c) the summary of sensitivity range.
SOI 슬롯 광도파로 기반 2×2 Balanced-Bridge Mach-Zender 간섭 구조를 바이오·케미컬 센서로 응용하기 위해서는 다음과 같은 설계절차를 제안한다.
첫째: 센싱 물질과 예상되는 굴절률을 고려해서 균일 또는 표면 센싱을 적용할 것인지 결정한다.
둘째: 측정에 사용될 광원의 파장과 주어진 공정 여건에 따라에 따라 최적화된 슬롯 광 도파로의 제원을 결정한다. 즉 슬롯의 폭, 레일의 두께 및 폭.
셋째: 2×2 Balanced-Bridge Mach-Zender 간섭 구조에서 (Fig.3 참조) 동일한 두 출력 광 파워를 유지할 수 있도록 3-dB 결합기의 간격 및 길이를 결정하고, 단일 소자구조가 차지하는 면적을 고려해서 채널 광도파로의 길이를 결정한다.
넷째: 센싱 물질의 굴절률 값의 크기에 따라 가급적 선형 특성이 유지될 수 있도록 센싱 영역의 길이를 결정한다. 굴절률 값이 클수록 센싱 영역의 길이를 짧게 설계한다.
5. 결 론
최적화된 SOI슬롯 광 도파로 기반 2×2 balanced-bridge Mach−Zehnder 간섭 구조를 이용해서 균일 및 표면 센싱을 수행할 수 있는 집적광학 바이오·케미컬 센서 구조를 제시하고, 3-dB 결합기와 채널 광 도파로의 전달 매트릭스를 활용해서 두출력 광 파워에 대한 수식들을 유도, 검토하였으며, 이 식들을 활용해서 동일한 출력 광 파워를 분배할 수 있도록 결합기 길이를 결정하였다. 제안된 센서 구조에서 균일 및 표면 센싱이 수행될 수 있도록 센싱 영역의 광 도파로 구조들이 분석물질의 굴절률 및 두께로부터 영향을 받을 수 있도록 적절한 구조를 제안하였고, Photon Design 사의 FIMMWAVE, FIMMPROP를 이용해서 두 출력 광 파워의 분포에 대해서 전산해석을 수행하였다.
균일 센싱에서 1.33−1.36 범위의 분석물질 굴절률이 두 출력광 파워 분포에 미치는 영향을 정량적으로 도출하였고, 이를 활용해서 각 출력 또는 두 출력 차를 기반으로 감도를 계산하였으며, 전자는7.5796−19.0305[au/RIU], 후자는 15.2601−38.1351[au/RIU] 감도의 분포를 확인할 수 있었다. 또한 센싱 영역의 길이가 감도에 미치는 영향도 체계적으로 분석하였다. 한편 표면 센싱에서는 1−20 nm 범위의 특정 분석물질 두께가 광 파워 출력 분포에 미치는 영향을 정량적으로 검토하였으며, 두 출력 광파워 분포로부터 감도를 계산하였으며, 이 경우에도 센싱 영역의 길이가 미치는 영향도 검토하였다. 두 출력 P1, P2 각각에 기반한 경우1.337 굴절률의 감도는 -2.2490−-3.5854[au/RIU], 1.2194−3.8012[au/RIU] 분포로 계산되었으며, 두 출력 차에 기반한 경우에는 4.8048−7.0694[au/RIU] 감도 범위가 확인되었다. 끝으로 2×2 Balanced-Bridge Mach-Zehnder 간섭 구조 설계에 대한 구체적인 절차를 제시하였으며, 실리콘 포토닉스와 microfluidics공정을 활용할 경우 제안된 구조로 소자를 구현할 수 있다.
Acknowledgments
이 논문은 한국연구재단 이공학개인기초연구 (2018-R1D1A1B07049908) 연구비 지원으로 수행되었습니다.
REFERENCES
-
X. Fan, L. White, S. Shopova, H. Zhu, J. Suter, and Y. Sun, “Sensitive optical biosensors for unlabeled targets: A review”, Anal. Chemi. Acta., Vol. 620, No. 1-2, pp. 8-26, 2008.
[https://doi.org/10.1016/j.aca.2008.05.022]

-
R. Chandrasekar, Z. J. Lapin, A. S. Nichols, R. M. Braun, and A. W. Fountain, “Photonic integrated circuits for Department of Defense-relevant chemical and biological sensing applications: state-of the-art and future outlooks”, Opt. Eng., Vol. 58, No. 2, pp. 0220901(1)-022090(12), 2019.
[https://doi.org/10.1117/1.OE.58.2.020901]

-
F. Prieto, B, Sepulveda, A. Calle, A. Llobera, C. Domınguez, A. Abad, A. Montoya, and L. M. Lechuga, “An integrated optical interferometric nanodevice based on silicon technology for biosensor applications”, Nanotechnol., Vol. 14, No. 8, pp, 907–912, 2003.
[https://doi.org/10.1088/0957-4484/14/8/312]

-
P. Munoz, G. Mico, L. A. Bru, D. Pastor, D. Perez, J. D. Domenech, J. Ferandez, R. Banos, B. Gargallo, R. Alemany, A. M. Sanchez, J. M. Cirere, R. Mas, and C. Dominguez, “Silicon Nitride Photonic Integration Platforms for Visible, Near-Infrared and Mid-Infrared Applications”, Sens., Vol. 17, pp. 2088(1)-2088(25), 2017.
[https://doi.org/10.3390/s17092088]

-
K. Worhoff, R. G. Heideman, A. Leinse, and M. Hoekman, “TriPlex: a versatile dielectric photonic platform”, Adv. Opt. Tech., Vol. 4, No. 2, pp. 189-207, 2015.
[https://doi.org/10.1515/aot-2015-0016]

-
D. L. Blumental, R. Heidman, D. Geuzberoek, A. Leinse, and C. Roeloffzen, “Silicon Nitride in Silicon Photonics”, Proc. of IEEE., Vol. 106, USA, pp. 2209-2231, 2018.
[https://doi.org/10.1109/JPROC.2018.2861576]

-
K. Zinoviev, A. B. Gonzalez-Guerrero, C. Domınguez, and L. M. Lechuga, “Integrated Bimodal Waveguide Interferometric Biosensor for Label-Free Analysis”, J. Lightwave Technol., Vol. 29, No. 13, pp. 1926–1930, 2011.
[https://doi.org/10.1109/JLT.2011.2150734]

-
V. R. Almeida, Q. Xu, C. A. Barrios, and M. Lipson, “Guiding and confining light in void nanostructure”, Opt. Lett., Vol. 29, No. 11, pp. 1209-1211, 2004.
[https://doi.org/10.1364/OL.29.001209]

-
T. Baehr-Jones, M. Hochberg, C. Walker, and A. Scherer, “High-Q optical resonator in silicon-on-insulator-based slot waveguides”, Appl. Phys. Lett. Vol. 86, No. 8, pp. 081101(1)-08110(3), 2005.
[https://doi.org/10.1063/1.1871360]

-
N. N. Feng, J. Michel, and L. C. Kimerling, “Optical Field Concentration in Low-Index Waveguides”, IEEE J. Quant. Elec., Vol. 42, No. 9, pp. 883-888, 2006.
[https://doi.org/10.1109/JQE.2006.880061]

-
P. Steglich, “Silicon-On-Insulator Slot Waveguides: Theory and Applications in Electro-Optics and Optical sensing”, Emerg. Waveguide Technol., pp. 188-210, 2018.
[https://doi.org/10.5772/intechopen.75539]

-
C. Koos, P. Vorreau, T. Vallaitis, P. Dumon, W. Bogaerts, R. Baets, B. Esembeson, I. Biaggio, T. Michinobu, F. Diederich, W. Freude, and J. Leuthold, “All-optical high-speed signal processing with silicon-organic hybrid slot waveguides”, Nat. Photonics., Vol. 3, No. 4, pp. 216-219, 2009.
[https://doi.org/10.1038/nphoton.2009.25]

-
M. Roussey, L. Ahmadi, S. Pélisset, M. Häyrinen, A. Bera, V. Kontturi, J. Laukkanen, I. Vartiainen, S. Honkanen, and M. Kuittinen, “Strip-loaded horizontal slot waveguide”, Opt. Lett., Vol. 42, No. 2, pp. 211-214, 2017.
[https://doi.org/10.1364/OL.42.000211]

-
H. Zengzhi, Y. Zhang, C. Zeng, D. Li, M. S. Nisar, J. Yu, and J. Xia, “High Confinement Factor Ridge Slot Waveguide for Optical Sensing”, IEEE Phot. Technol. Lett., Vol. 27, No. 22, pp. 2395-2398, 2015.
[https://doi.org/10.1109/LPT.2015.2466595]

-
R. Singh and V. Priye, “Si3N4-SiO2 Based Curve Slot Waveguide for High Confinement Factor and Low Mode Effective Area along with Biosensing Alpplication”, Silicon, Vol. 14, No. 3, pp. 859-867, 2021.
[https://doi.org/10.1007/s12633-020-00927-y]

-
C. A. Barrios, “Optical Slot-Waveguide Based Biochemical Sensors”, Sensors, Vol. 9, No. 6, pp. 4751-4765, 2009.
[https://doi.org/10.3390/s90604751]

-
T. Dar, J. Holma, B. M. Azizur Rahman, and M. Rajarajan, “Label-free slot- waveguide biosensor for the detection of DNA hybridization”, Appl. Opt., Vol. 51, No. 34, pp. 8195-8202, 2012.
[https://doi.org/10.1364/AO.51.008195]

-
E. Luan, H. Shoman, D. M. Ratner, K. C. Cheung, and L. Chrostowski, “Silicon Photonics Biosensors Using Label-Free Detection”, Sensors, Vol. 18, No. 10, pp. 3519(1)-3519(12), 2018.
[https://doi.org/10.3390/s18103519]

-
F. Brosinger, H. Freimuth, M. Lacher, W. Ehrfeld, E. Gedig, A. Katerkamp, F. Spener, and K. A. Cammann, “Label-free affinity sensor with compensation of unspecific protein interaction by a highly sensitive integrated optical Mach–Zehnder interferometer on silicon”, Sens. Actuators B, Vol. 44, No. 1-3, pp. 350-355, 1997.
[https://doi.org/10.1016/S0925-4005(97)00226-8]

-
Q. Liu, X. Tu, K. W. Kim, J. S. Kee, Y. Shin, K. Han, Y.-J. Yoon, G.-Q. Lo, and M. K. Park, “Highly sensitive Mach-Zehnder interferometer biosensor based on silicon nitride slot waveguide”, Sens. Act. B: Chem., Vol. 188, pp. 681-683, 2013.
[https://doi.org/10.1016/j.snb.2013.07.053]

- H. S. Jung, “Study on the Design and Performance of Integrated-Optic Biosensor utilizing the Multimode Interferometer based on Si3N4 Rib-Optical Waveguide and Evanescent-Wave”, J. IKEEE, Vol. 24, No. 2, pp. 38-47, 2020.
-
X. Li, Z. Zhang, S. Qin, T. Wang, F. Liu, M. Qiu, and Y, Su, “Sensitive label-free and compact biosensor based on concentric silicon-on-insulator microring resonators”, Appl. Opt., Vol. 48, No. 25, pp. F90-F94, 2009.
[https://doi.org/10.1364/AO.48.000F90]

-
R. Zeng, B. Wang, Z. Bu, B. Ben Niu, and Y. Hua, “Integrated optical E-field sensor based on balanced Mach-Zehnder interferometer”, Opt. Eng. Vol. 50, No, 11, p. 114404, 2011.
[https://doi.org/10.1117/1.3651809]

-
H. S. Jung, “An Integrated Photonic Electric-Field Sensor Utilizing a 1×2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Diple Patch Antenna”, Cryst., Vol. 9, No. 9, pp. 459(1)-459(11), 2019.
[https://doi.org/10.3390/cryst9090459]

-
H. S. Jung, “Optimization of vertical SOI slot optical waveguide with confinement factor and sensitivity for integrated-optical biochemical sensors,” J. Sens. Sci. Technol. Vol. 30, No. 3, pp. 131-138, 2021.
[https://doi.org/10.46670/JSST.2021.30.3.131]

- Photon Design Ltd., FIMMWAVE v6.6.0, Oxford, United Kingdom, 2018.
-
Y. Liu, M. Kong, and Y. Jiang, “Transverse magnetic modes in planar slot waveguides”, J. Opti. Soci. B Am., Vol. 32, No.10, pp. 2052-2060, 2015.
[https://doi.org/10.1364/JOSAB.32.002052]

-
Y. Jiang, M. Kong, C. Liu, Y. Liu, and Y. Wang, “Transverse electric modes in planar slot waveguides”, J. Modern Optics., Vol. 65, No. 1, pp. 111-118, 2018.
[https://doi.org/10.1080/09500340.2017.1377307]