다중모드 센서 신호 처리 프로세서의 FPGA 기반 설계 및 구현
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Internet of Things (IoT) systems process signals from various sensors using signal processing algorithms suitable for the signal characteristics. To analyze complex signals, these systems usually use signal processing algorithms in the frequency domain, such as fast Fourier transform (FFT), filtering, and short-time Fourier transform (STFT). In this study, we propose a multi-mode sensor signal processor (SSP) accelerator with an FFT-based hardware design. The FFT processor in the proposed SSP is designed with a radix-2 single-path delay feedback (R2SDF) pipeline architecture for high-speed operation. Moreover, based on this FFT processor, the proposed SSP can perform filtering and STFT operation. The proposed SSP is implemented on a field-programmable gate array (FPGA). By sharing the FFT processor for each algorithm, the required hardware resources are significantly reduced. The proposed SSP is implemented and verified on Xilinx’s Zynq Ultrascale+ MPSoC ZCU104 with 53,591 look-up tables (LUTs), 71,451 flip-flops (FFs), and 44 digital signal processors (DSPs). The FFT, filtering, and STFT algorithm implementations on the proposed SSP achieve 185x average acceleration.
Keywords:
Sensor signal processor, FFT, Filtering, STFT, FPGA1. 서 론
최근 삶의 질을 향상시키는 IoT (Internet of Things), 스마트가전 등의 분야에서 센서를 활용한 다양한 응용이 연구되고 있다 [1-2]. 여러 응용을 위해 다양한 센서가 사용되는 시스템에서, 센서 신호는 센서의 고유 특성, 취득 환경, 응용에 따라 적절한 신호 처리 알고리즘으로 처리되어야 한다. 예를 들어, 특정 주파수 대역의 잡음이 감지되는 신호는 해당 주파수 영역에 대한 필터링이 수행되어야 하고 시간에 따라 주파수 성분이 변하는 센서 신호는 시간-주파수 분석 알고리즘으로 분석되어야 한다.
푸리에 변환 (Fourier transform), 필터링, 그리고 STFT (short-time Fourier transform)는 대표적인 센서 신호 처리 알고리즘이며 복잡한 신호를 분석하기 위해 사용된다. 푸리에 변환은 시간영역의 신호를 주파수 영역으로 변환하는 것이다. STFT는 대표적인 시간-주파수 분석 기술 중 하나로, 입력 신호를 일정 길이로 나누어 윈도우 함수를 곱한 다음, 푸리에 변환을 수행하는 것이다. STFT 결과인 2D 스펙트로그램 이미지는 레이다, IMU(inertial measurement unit), 생체신호를 처리하는 등 여러 응용에 적용된다 [3-5]. 필터링은 센서 신호의 취득 환경에 따라 발생하는 특정 주파수 대역의 잡음을 제거하거나, 필요한 주파수 대역만을 유지한다. Fig. 1은 다양한 센서에 대한 세 가지 신호처리 응용 예시를 보여준다. 푸리에 변환은 표적에 반사된 신호의 주파수 성분이 변화하는 레이다 신호의 특성을 활용하여 표적의 거리와 속도를 표현하는 거리-도플러 맵을 생성하는 데 사용된다 [6]. 필터링은 음성 신호의 잡음을 제거하고, STFT는 제스처에 대한 생체신호의 특징을 추출한다.
IoT 시스템과 스마트 가전제품 등에 적용되는 센서 기반 엣지 디바이스들은 편리함을 위해 실시간 처리와 저전력 설계가 요구된다 [7]. 특히 헬스케어 관련 시스템의 경우 센서 신호에 대한 의료 기능은 불필요한 지연이 없는 고속 처리가 필수적으로 요구된다 [8].
기본적으로 신호와 필터 계수의 합성곱을 통해 이루어지는 필터링은 연산 복잡도가 높다. 이를 극복하기 위해, 시간 영역에서의 합성곱 연산은 주파수 영역에서의 곱셈으로 대체되어 연산 복잡도를 크게 줄일 수 있다. 결국 위에서 언급된 세 가지 신호 처리 알고리즘은 모두 주파수 영역에서의 신호 처리로 구현될 수 있다. 이 신호 처리 과정들은 푸리에 변환을 기반으로 이루어지기 때문에 디지털 신호의 푸리에 변환인 DFT (discreteFourier transform)를 가속한 FFT (fast Fourier transform) 프로세서를 설계함으로써 가속될 수 있다. 필터링과 STFT는 모두 FFT 연산과 복소 곱셈의 조합으로 이루어지기 때문에, 단일 프로세서에 FFT 프로세서와 곱셈기를 통합하면 앞서 언급된 세 가지 신호 처리 알고리즘을 모두 고속으로 처리할 수 있다. 따라서 본 논문에서는 FFT 프로세서 기반 SSP (sensor signal processor)를 제안한다. 제안된 SSP는 고속, 저전력 설계를 위해 FPGA(field-programmable gate array)에 구현되었으며 FFT 프로세서와 하나의 복소 곱셈기로 구성된다. FFT 프로세서는 R2SDF(radix-2 single path delay feedback) 파이프라인 구조로 설계되어 여러 FFT 구조에 대한 요구사항 중 속도와 면적을 절충한다. 또한 64/128/526/512/1,024/2,048 길이에 대한 가변 길이 FFT연산을 지원한다. 결과적으로 제안된 SSP는 FFT 프로세서에 최소의 하드웨어 자원만을 추가함으로써 다양한 형태의 신호 처리 알고리즘을 선택적으로 수행할 수 있도록 구현되었다.
본 논문의 구성은 다음과 같다. 2장에서는 언급된 세 가지 신호 처리 알고리즘에 대해 간략히 소개한다. 3장에서는 제안된 SSP의 구조에 대해 설명한다. 4장에서는 제안된 SSP의 하드웨어 구현 및 검증 결과를 제시하고, 5장에서 본 논문의 결론을 맺는다.
2. 주파수 영역 신호 처리 알고리즘
2.1 푸리에 변환
디지털 신호 처리에서의 푸리에 변환인 DFT는 식 (1)과 같이 정의된다.
| (1) |
X는 주파수 영역의 신호, x는 시간 영역의 신호 그리고 N은 신호 길이이다. FFT는 회전 인자의 특성을 활용하여 DFT의 연산 복잡도를 감소시킨 신호 처리 알고리즘이다. DFT 연산은 N2만큼의 곱셈이 필요하지만, 회전 인자의 특성을 활용한 FFT는 Nlog2N만큼의 곱셈이 수행되며 이 가속 효과는 신호 길이가 길수록 극대화된다. FFT는 이러한 효율성 때문에 디지털 신호 처리의 주파수 분석에 자주 사용된다.
반대로, 주파수 영역의 신호를 시간 영역의 신호로 변환하는 역 푸리에 변환은 식 (2)와 같이 정의된다.
| (2) |
역 푸리에 변환 또한 FFT와 같은 방법을 사용하여 iFFT (inverse FFT)로 가속될 수 있다.
2.2 필터링
필터링은 원하는 주파수 대역의 신호를 증폭하거나 감쇄하는 신호 처리 알고리즘이다. 시간 영역에서의 합성곱으로 구현되는 필터링은 수식 (3)과 같다.
| (3) |
xfil는 처리된 신호, h는 시간 영역의 필터 계수이다. DFT와 같이 연산량이 많은 합성곱은 주파수 영역에서의 곱셈으로 대체될 수 있다. N2만큼의 곱셈이 필요한 합성곱 연산은 FFT와 곱셈을 통해 2Nlog2N+N만큼의 곱셈으로 대체된다.
2.3 단시간 푸리에 변환
FFT를 통해 신호의 주파수 성분은 분석할 수 있지만, 시간에 따라 주파수 성분이 변화하는 신호는 분석하기 어렵다. STFT는 이러한 FFT의 한계를 극복하기 위해 사용된다. STFT는 신호를일정 구간 간격으로 나누고, 윈도우 함수를 곱하여 FFT를 수행한다. STFT는 식 (4)와 같이 정의된다.
| (4) |
w는 윈도우 함수, m은 윈도우 지연 시간이다. STFT를 위해 신호를 나누어 FFT를 적용하면, 각 구간 당 신호 양 끝의 불연속성 때문에 스펙트럼 누설 (spectral leakage)이 발생한다. 따라서 일반적으로 STFT는 신호의 양 끝의 진폭이 0이거나 0에 수렴하는 윈도우 함수를 각 구간에 곱하여 FFT를 수행한다. STFT의 결과는 시간 축과 주파수 축에 대한 2D 스펙트로그램 이미지로 생성되며, 시간-주파수 분석에 효과적으로 사용된다.
3. 제안된 센서 신호 처리기
3.1 FFT 프로세서
제안된 SSP는 하드웨어 시스템으로 구현되며, 수행하는 신호처리 알고리즘들은 FFT 연산의 비중이 가장 크다. 따라서 FFT 프로세서의 구조 설계는 제안된 SSP의 핵심 부분이며, 제안된 SSP의 설계 목적인 가속 성능과, 엣지 디바이스에서의 구현을 위한 시스템 면적이 모두 고려되어야 한다. 결과적으로 FFT 프로세서는 속도와 면적의 trade-off 관계를 절충하는 R2SDF 파이프라인 구조로 설계되었다. 설계된 FFT 프로세서의 구조는 Fig. 2와 같다. 제안된 SSP는 최대 2,048 길이의 FFT를 수행하기 때문에 파이프라인 구조의 FFT 프로세서는 총 11 stage로 구성되었다. 각 stage는 SBF (single butterfly)와 회전 인자 곱셈기, 지연 레지스터로 구성된다. Stage 1에서 지연 레지스터는 입력을 1,024 만큼 지연시키며, stage가 지날수록 지연 시간은 2배씩 감소한다. 또한 64-2,048 길이의 신호에 대해 FFT를 선택적으로 수행하기 위해 FFT프로세서의 입력은 stage 1뿐만 아니라 각 stage의 입력으로 연결된다.
식 (1-2)에 의하면 iFFT 연산에서 곱해지는 회전 인자는 FFT연산의 회전 인자에 대한 켤레 복소수이기 때문에, 입출력 데이터의 실수부분과 허수부분의 교환을 통해 iFFT 연산은 FFT 프로세서로 구현될 수 있다. FFT 연산을 통한 iFFT의 구현은 식 (5)와 같다.
| (5) |
따라서 식 (5)의 을 구현하기 위해 stage 끝단 마다 2를 나누어 주는 연산이 선택적으로 수행된다.
3.2 SSP 구조
FFT, iFFT, 필터링 그리고 STFT와 같은 주파수 영역의 신호처리 알고리즘들을 단일 프로세서에 구현하기 위해, 제안된 SSP는 FFT 프로세서와 복소 곱셈기를 조합하여 설계되었다. 제안된 SSP의 구조는 Fig. 3과 같다. 제안된 SSP는 FFT 프로세서 (R2SDF FFT Processor), 복소 곱셈기 (Complex Multiplier), 계수 버퍼 (Coefficient Buffer) 그리고 제어기 (SSP Controller)로 구성된다. 입력 버퍼 (Input Buffer)는 64부터 2,048 길이의 센서 데이터를 저장하고, 출력 버퍼 (Output Buffer)는 FFT 프로세서의 연산 결과를 저장한다. 계수 버퍼는 필터링에 사용되는 필터 계수 또는 STFT를 위한 윈도우 함수를 저장한다. 입력 버퍼와 계수 버퍼는 DRAM에서 데이터를 전달받고, 출력 버퍼의 값은 DRAM으로 전달된다. 제안된 SSP는 하나의 수를 표현하는 데 16 비트가 사용된다. 따라서 세 가지 버퍼들은 모두 DRAM과의 통신 과정에서 한 번에 2개의 복소수를 교환하고 최대2,048개의 데이터를 저장하기 위해 64×1,024 의 형태로 구성된다. 제안된 SSP는 한 번에 하나의 복소수를 처리하기 위해 버퍼들로부터 읽은 데이터를 multiplexer를 통해 하나씩 선택한다.
제안된 SSP에서 각 신호 처리 알고리즘들은 다음과 같이 수행된다. FFT 연산의 경우, 제안된 SSP는 입력 버퍼를 읽고, MUX를 통해 하나씩 선택된 센서 데이터를 FFT 프로세서로 전달한다. FFT 프로세서는 파이프라인 구조로 FFT 연산을 수행하여 결과를 출력 버퍼에 저장한다. FFT 연산 중 복소 곱셈기와 계수 버퍼는 사용되지 않는다. iFFT 연산의 경우, 입력 버퍼의 센서 데이터는 실수부분과 허수부분이 교환된 형태로 FFT 프로세서에 전달된다. FFT 프로세서는 stage 연산 마다 2를 나누고, 결과를 다시 실수부분과 허수부분을 교환하여 출력 버퍼에 저장한다. 그 외의 연산은 FFT와 같다. 필터링의 경우, 시간 영역의 센서 데이터는 먼저 FFT 연산을 통해 주파수 영역으로 변환되어 출력 버퍼에 저장된다. 출력 버퍼에 저장된 주파수 영역의 센서 데이터는 복소 곱셈기를 통해 계수 버퍼의 필터 계수와 곱해지는 주파수 영역의 필터링이 수행되고, iFFT 연산을 통해 다시 시간 영역으로 변환되어 출력버퍼에 저장된다. STFT의 경우, 입력 버퍼의 센서 데이터는 계수 버퍼에 저장된 윈도우 함수와 곱해진 뒤 FFT 연산이 수행되어 출력 버퍼에 저장된다. 이 과정을 통해 해당 시간에 대한 주파수 분석 결과인 하나의 column이 생성되며, 센서 데이터의 업데이트와 반복 연산을 통해 여러 column으로 구성된 2D 스펙트로그램이 완성된다.
3.3 제안된 SSP에서의 수 표현
디지털 시스템에서 수의 표현 방법은 응용에 따라 다양한 형태로 결정된다. 고정소수점 기반 FFT 프로세서는 낮은 SQNR(signal-to-quantization-noise ratio)과 입력에 따른 overflow에 의해 제한되는 dynamic range때문에 고해상도, 고성능 시스템 분야에 적절하지 않다 [9]. 반면, 부동소수점 기반 설계는 정밀연산을 고려할 때 다양한 문제를 최적화하기 위해 사용된다[10]. 다양한 센서에 대한 응용을 목표로 하는 제안된 SSP는 센서와 응용의 특성에 따라 신호 처리 과정의 정보 손실이 치명적일 수 있기 때문에 높은 정밀도를 필요로 한다. 제안된 SSP는 정밀도를 위해 부동소수점 수체계를 사용한다. 그러나 저전력 임베디드 시스템에서 높은 비트 폭의 부동소수점 연산은 전력 소비를 증가시킨다. 이를 해결하기 위해 더 적은 비트 폭을사용하게 되면 연산 회로가 보다 간단해지고, 메모리 대역폭을 줄일 수 있어 에너지 소비를 줄일 수 있다 [11]. 따라서 제안된 SSP는 높은 정밀도와 저전력 설계를 위해 64, 32비트가 아닌 16비트 부동소수점 수체계를 사용한다. 16비트 부동소수점수체계에서 수는 1비트의 부호부분 (sign), 5비트의 가수부분(exponent), 그리고 10비트의 지수부분 (mantissa)으로 구성된다. 부호, 가수, 지수부분은 MSB (most significant bit)부터 LSB(least significant bit)까지 순서대로 배열된다. 16비트 부동소수점 수체계의 값은 식 (6)과 같이 계산되며, Fig. 4와 같이 표현된다.
| (6) |
예를 들어, 값 2.75는 식 (6)에 의해 (–1)0×(1+384/210)×2(1)로 계산되며 부호 부분은 0, 가수부분은 16, 지수부분은 384이다. 따라서 2.75는 16비트 부동소수점 수체계에서 (0100000110000000)2로 표현된다. 이에 따라 제안된 SSP의 정밀도를 측정하기 위해 레이다, 음성, 생체 신호를 다양한 센서로 취득하여 실험한 결과, 약 54 dB의 높은 SQNR 성능이 확인되었다.
4. 구현 및 검증 결과
4.1 구현 결과
제안된 SSP는 Verilog HDL (hardware description language)을사용하여 Xilinx's Zynq Ultrascale+ MPSoC ZCU104 FPGA에서구현 및 검증되었다 [12]. 구현된 시스템은 최대 150 MHz의 클락 주파수에서 동작할 수 있다. 제안된 SSP는 53,591 개의 LUTs(look-up tables), 71,451 개의 FFs (flip-flops), 그리고 44개의 DSPs(digital signal processors)로 구현되었다. 유닛당 하드웨어 자원사용량을 Table 1에 나타내었다. FFT 프로세서를 제외한 유닛은 FFT 프로세서의 2.3%의 LUTs, 0.3%의 FFs 그리고 9.1%의DSPs만을 사용하여 구현되었다. FFT 프로세서는 FFT 연산만을 수행할 수 있지만, 제안된 SSP는 최소한의 회로만을 추가하여 필터링과 STFT까지 수행할 수 있는 시스템으로 구현되었다
4.2 검증 결과
Fig. 5는 제안된 SSP의 FPGA 검증을 위해 구성된 시스템을 나타낸다. 구성된 시스템은 64 비트 AXI (advanced extensible interface) 버스를 통해 마이크로프로세서 (Micro-processor), DRAM과 통신한다. Master 인터페이스 (Master Interface)는 DRAM으로부터 센서 데이터, 필터 계수, 윈도우 함수 등을 입력 버퍼 (Input Buffer)로 전달하고, 신호 처리 결과가 저장된 출력 버퍼 (Output Buffer)의 데이터를 DRAM으로 전달한다. AXI 버스의 데이터 폭은 64 비트이기 때문에, master 인터페이스를 통해 데이터를 주고받는 버퍼들의 폭 또한 64 비트이다. 마이크로프로세서는 slave 인터페이스 (Slave Interface)를 통해 시작신호와 수행할 신호 처리에 대한 매개변수 등을 제안된 SSP로 전달한다.
마이크로프로세서가 전달하는 신호 처리에 대한 매개변수는 수행할 신호 처리 알고리즘, FFT 길이, 신호 처리 횟수 등이 있다. 제안된 SSP는 이와 같은 정보들을 활용하여 DRAM에서 적절한 데이터를 받아 필요한 횟수만큼 신호 처리를 수행한다. 신호 처리 횟수는 FFT프로세서가 FFT 길이의 신호를 몇 번 처리할 것인지 의미하고, STFT에서는 생성할 스펙트로그램의 열 개수를 의미한다. 이 정보는 16 비트 데이터로 전달되기 때문에, 제안된 SSP는 시작 신호 한 번으로 최대 216 = 65,536 만큼의 신호 처리를 수행할 수 있다.
이와 같이 구성된 시스템을 실제 센서 데이터를 사용하여 검증하기 위해 sEMG (surface electromyography) 센서와 CW (continuous wave) 레이다 센서가 사용되었다. sEMG 신호는 생체 신호 중 하나로, 직관적인 근육 활동 정보를 포함한다. CW 레이다 센서는 전파를 연속적으로 방사하여 반사된 신호의 도플러 성분을 통해 표적의 속도를 추출할 수 있다. sEMG 센서는 Fig. 6(a)의 DFrobot의 Gravity [13]를 사용하였고, CW 레이다 센서는 Fig. 6(b)의 Infineon Tech사의 Sense2GoL [14]이 사용되었다.
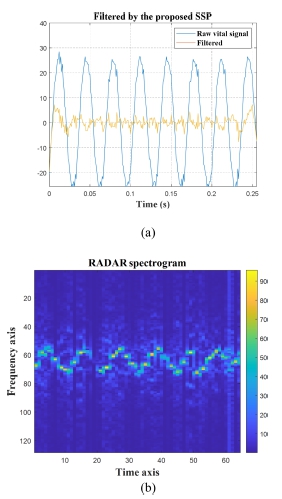
Fig. 7은 제안된 SSP가 sEMG 신호를 필터링한 결과와, CW신호를 STFT한 결과를 나타낸다. 1 kHz의 샘플링 속도로 0.256초 동안 취득된 sEMG 신호는 40 Hz 차단 주파수에 대한 고역통과 필터 계수를 적용하여 필터링 되었다. CW 신호는 1 kHz의 샘플링 속도로 취득되어 128 FFT 길이에 대해 64의 overlap으로 STFT 되었다. Fig. 7(a)에서 필터링 결과로 저주파 성분이 제거된 파형이 관찰되었고, Fig. 7(b)에서 STFT를 통해 시간에 대한 표적의 속도 변화를 확인할 수 있었다.
4.3 제안된 SSP의 가속 성능
제안된 SSP를 평가하기 위해, 하드웨어와 소프트웨어에서의 신호 처리를 조합하여 세 가지 경우에 대한 가속 성능을 평가하였다. 첫 번째 경우는 모든 신호 처리 과정을 ARM Cortex-A53에서 소프트웨어 프로그램을 통해 수행한다. 두 번째 경우는 신호 처리 과정 중 FFT 연산만을 제안된 SSP에서 수행하고, 곱셈과 같은 나머지 연산은 소프트웨어에서 수행하였다. 세 번째 경우는 모든 신호 처리 과정을 제안된 SSP에서 수행하였다. Table 2에서 이 세 가지 경우에 대한 각 신호 처리 알고리즘의 수행 시간을 나타낸다.
제안된 SSP는 최대 동작 주파수인 150 MHz 클락 주파수에서 동작하였다. Table 2에 제시된 FFT와 필터링의 지표는 2,048 길이에 대한 연산 시간이며, STFT의 지표는 2,048×64 의 스펙트로그램을 생성하는 연산 시간이다. FFT 연산은 제안된 SSP를 통해 연산 속도가 약 174배 증가하였다. 필터링과 STFT는 FFT 연산만을 제안된 SSP로 가속하였을 때 연산 속도가 각각 39, 23배 증가하였고, 모든 연산을 제안된 SSP로 가속하였을 때 각각 202, 178배 증가하였다. 복소 곱셈기 등 FFT 프로세서를 제외한 회로로 인한 가속 성능은 각각 5.2, 7.7배로 확인되었다.즉 제안된 SSP는 FFT 프로세서에 적은 회로를 추가 통합함으로써 여러 신호 처리 알고리즘을 선택적으로 수행함과 동시에 높은 가속 성능을 달성하였다.
5. 결 론
일반적으로 FPGA에 구현된 하드웨어 시스템은 특정 용도에 최적화되어 설계되기 때문에 처리 속도가 빠르고 전력 소모가 적지만, 재구성이 어렵다는 한계가 있다. 특히 다양한 센서를 활용하는 시스템의 경우, 각 센서의 신호 처리기가 분리되어 병렬적으로 설계된다면 자원이 제한된 엣지 디바이스 또는 임베디드 시스템에서의 구현에 어려움이 발생한다. 따라서 본 논문은 FFT, 필터링, STFT와 같은 주파수 영역의 신호 처리 알고리즘이 FFT 프로세서를 기반으로 구현될 수 있다는 점을 고려하여, FFT 프로세서 기반의 다중모드 SSP를 설계하고, FPGA기반 구현 결과를 제시한다. 제안된 SSP는 하나의 FFT 프로세서와 복소 곱셈기로 구성됨으로써 세 가지 주파수 영역의 신호 처리 알고리즘을 선택적으로 수행할 수 있다. 따라서 제안된 SSP는 특정 응용에 제한되지 않고, 재구성 가능하여 주파수 영역 신호처리를 필요로 하는 다양한 센서 기반 응용에 적용될 수 있다. FPGA에 구현된 제안된 SSP는 세 가지 신호 처리 알고리즘에 대해 평균 185배의 가속 성능을 달성하였고, 연산 회로가 공유됨으로써 자원이 제한된 하드웨어 시스템에 적절하다.
Acknowledgments
본 연구는 산업통상자원부의 기술혁신사업 (No.00144288, 00144290)의 일환으로 수행되었으며, CAD tool은 IDEC에 의해 지원되었음.
REFERENCES
-
Y. Perwej, M. A. AbouGhaly, B. Kerim, and H. A. M. Harb, “An Extended Review on Internet ot Things (IoT) and its Promising Applications”, Commun. Appl. Electronics (CAE), ISSN, Vol. 7, No. 26, pp. 8-22, 2019.
[https://doi.org/10.5120/cae2019652812]

-
N. K. Suryadevara, and S. C. Mukhopadhyay, “Wireless Sensor Network Based Home Monitoring System for Wellness Determination of Elderly”, IEEE Sens. J., Vol. 12, No. 6, pp. 1965-1972, 2012.
[https://doi.org/10.1109/JSEN.2011.2182341]

-
S. Kang, H. Kim, C. Park, Y. Sim, and Y. Jung, “sEMG-based Hand Gesture Recognition Using Binarized Neural Network”, Sensors, Vol. 23, No. 3, pp. 1436-1451, 2023.
[https://doi.org/10.3390/s23031436]

-
M. Z. Arshad, D. Jung, M. Park, H. Shin, J. Kim, and K. Mun, “Gait-based Frailty Assessment using Image Representation of IMU Signals and Deep CNN”, Proc. of 2021 43rd Annual Int. Conf. IEEE Eng. in Med. Biol. Soc. (EMBC), pp. 1874-1879, 2021.
[https://doi.org/10.1109/EMBC46164.2021.9630976]

-
K. Abratkiewicz, P. Krysik, Z. Gajo, and P. Samczynski, “Target Doppler Rate Estimation Based on the Complex Phase of STFT in Passive Forward Scattering Radar”, Sensors, Vol. 19, No. 16, pp. 3627-3639, 2019.
[https://doi.org/10.3390/s19163627]

-
J. Heo, Y. Jung, S. Lee, and Y. Jung, “FPGA Implementation of an Efficient FFT Processor for FMCW Radar Signal Processing”, Sensors, Vol. 21, No. 19, pp. 6443-6458, 2021.
[https://doi.org/10.3390/s21196443]

-
N. N. Alajlan and D.M Ibrahim, “TinyML: Enabling of Inference Deep Learning Models on Ultra-Low-Power IoT Edge Devices for AI Applications”, Micromachines, Vol. 13, No. 6, pp. 851-872, 2022.
[https://doi.org/10.3390/mi13060851]

-
V. Aivaliotis, K. Tsantikidow, and N. Sklavos, “IoT-Based Multi-Sensor Healthcare Architectures and a Lightweight-Based Privacy Scheme”, Sensors, Vol. 22, No. 11, pp. 4269-4279, 2022.
[https://doi.org/10.3390/s22114269]

-
M. Wang, F. Wang, S. Wei, and Z. Li, “A pipelined area-efficient and high-speed reconfigurable processor for floating-point FFT/IFFT and DCT/IDCT computations”, Microelectronics J., Vol. 47, pp. 19-30, 2016.
[https://doi.org/10.1016/j.mejo.2015.11.004]

-
S. Mach, D. Rossi, G. Tagliavini, A. Marongiu, and L. Benini, “A Transprecision Floating-point Architecture for Energy-Efficient Embedded Computing”, Proc. of 2018 IEEE Int. Symp. Circuits Syst. (ISCAS), pp. 1-5, Florence, Italy, 2018.
[https://doi.org/10.1109/ISCAS.2018.8351816]

-
G. Tagliavini, S. Mach, D. Rossi, A. Marongiu, and L. Benini, “A Transprecision Floating-Point Platform for Ultra-Low Power Computing”, Proc. of 2018 Design, Autom. Test in Eur. Conf. Exhib. (DATA), pp. 1051-1056, Dresden, Germany, 2018.
[https://doi.org/10.23919/DATE.2018.8342167]

- https://www.xilinx.com/products/boards-and-kits/zcu104.html#overview, (retrieved on June. 21, 2023).
- https://www.dfrobot.com/product-1661.html/, (retrieved on June. 21, 2023).
- https://www.infineon.com/cms/en/product/evaluation-boards/demo-sense2gol/, (retrieved on June. 21, 2023).