초단기선 탑재 무인수상선의 협력 항법을 통한 무인잠수정의 위치인식 향상

1. 서 론

무인잠수정(unmanned underwater vehicle, UUV)은 수중에서 자율적으로 탐사 등의 임무를 수행하는 로봇 시스템이다. 무인잠수정의 성공적인 임무 수행을 위해 수중에서의 위치인식은 매우 중요하다. 그러나 무인잠수정은 기본적으로 자세방위기준장치(attitude heading reference system, AHRS), 도플러유속계(Doppler velocity log, DVL), 심도계(depth sensor) 등의 센서값을 적분하여 위치 및 자세를 계산하는 관성항법시스템(inertial navigation system, INS)[1]에 의존하기 때문에 위치 추정에 오차가 쌓일 수밖에 없다. 이를 해결하기 위해 주기적인 수면 부상으로 GPS 보정을 받을 수 있으나 장시간 깊은 수심에서 임무를 수행해야 하는 경우에는 이러한 부상 횟수를 줄이는 것이 바람직하다. 무인잠수정의 임무용으로 장착되어 있는 소나 센서를 이용하여 수중 지형 관측 정보를 기반으로 위치를 보정하는 방법들도 제안되었으나[2,3], 정밀한 수중 지형 지도를 사전에 얻기 어렵고, 국부 지형 정보를 생성하는 과정에서 여전히 오차가 누적된다는 문제가 있다. 이를 해결하기 위해서는 결국 절대적인 위치 보정 정보가 필요하며 본 논문에서는 무인잠수정을 추종하는 무인수상선이 있어 이러한 정보를 제공할 수 있다고 가정하였다. 구체적으로, 무인잠수정과 무인수상선에 각각 초단기선(ultra-short baseline, USBL) 송수신기를 장착하면 무인잠수정이 USBL의 관측 범위에 있는 동안에는 절대 위치 정보를 받을 수 있는데, 무인수상선에 장착된 USBL 트랜시버(transceiver)가 무인잠수정에 장착된 트랜스폰더(transponder)의 신호를 이용하여 음파거리(acoustic range)와 음파각(acoustic bearing)을 계산할 수 있기 때문이다. 하지만 이렇게 계산된 위치 정보에는 무인수상정의 GPS 및 음파거리와 음파각 추정에 따른 오차가 있기 때문에 센서 융합을 통해 정확도를 높여야 한다. 본 논문에서는 무인잠수정의 장시간 위치 추정을 위해 관성항법 정보와 수중지형 정보, 그리고 무인수상선의 USBL 정보를 SLAM(simultaneous localization and mapping)[4,5] 프레임워크 중 하나인 포즈그래프 최적화 기반으로 융합하는 방법을 제안하고자 한다.

2. UUV-USV 협력 항법

2.1 UUV 항법 시스템 설계

2.1.1 관성 항법

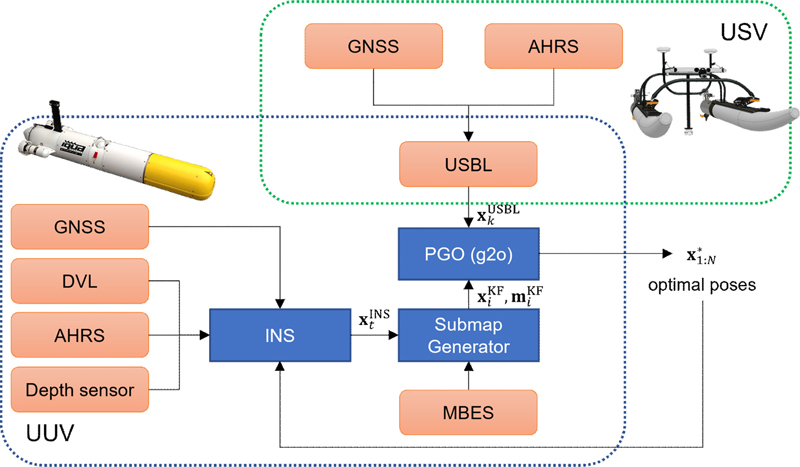
무인잠수정의 항법 시스템에 대한 전체 구조는 Fig. 1과 같으며 여기서는 먼저 무인잠수정의 기본 항법에 대해 설명한다. 무인잠수정은 수면에 있는 동안 GNSS 와 AHRS 정보를 이용하여 초기위치를 정렬할 수 있다. 이후 수중에서의 임무가 시작되면 AHRS와 DVL을 이용하여 관성 항법을 수행하며 $$ {\mathbf{x}}_t^{\mathrm{I}\mathrm{N}\mathrm{S}}$$를 계산한다. 무인잠수정의 항법 정보 추정에 대한 상태변수 벡터는 아래와 같다.

Fig. 1.

Overall framework of UUV pose graph optimization.

$\[ {\mathbf{x}}_t={\left[x,y,z,\theta ,\varphi ,\psi ,u,v,w,p,q,r\right]}^{\mathrm{T}} \]$

(1)

여기서 x_t의 각 요소는 무인잠수정의 시간 t에서의 3차원 위치, 자세(attitude), 선속도, 그리고 각속도이며 NED와 같은 로컬 지도 좌표계에서 표현한다. 상태 정보는 확장칼만필터에 의해 계산되며[6] AHRS와 DVL의 샘플링 주기에 맞춰 예측되고 갱신된다.

2.1.2 지형 기반 항법

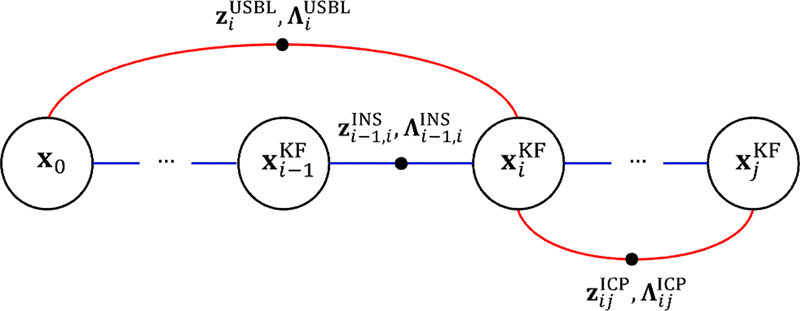
앞에서 생성된 $$ {\mathbf{x}}_t^{\mathrm{I}\mathrm{N}\mathrm{S}}$$는 추가적으로 지형 기반 항법을 위해 다중빔음향측심기(multi-beam echosounder, MBES)와 함께 활용된다. MBES는 수중의 지면에 대해 음향 신호를 발산하고 리턴되는 신호 강도를 검출하여 반사지점의 거리와 각을 측정할 수 있으며 2차원 라이다와 같이 센서 좌표계의 특정 평면 내에서 관측 대상에 대한 점군(point cloud) 데이터를 제공한다. 매 스캔마다 생성되는 MBES 점군을 시간 상 가장 가까운 $$ {\mathbf{x}}_t^{\mathrm{I}\mathrm{N}\mathrm{S}}$$를 이용하여 센서 좌표계에서 지도 좌표계로 변환하고 이를 특정시간 동안 취합하게 되면 수중 지형에 대한 로컬 서브맵(submap)을 만들 수 있다. 로컬 서브맵이 만들어지는 시점의 위치 및 자세값을 키프레임 $$ {\mathbf{x}}_i^{\mathrm{K}\mathrm{F}}$$로 정의하며 서브맵 $$ {\mathbf{m}}_i^{\mathrm{K}\mathrm{F}}$$과 함께 별도의 데이터로 저장한다. 무인잠수정의 지형 기반 항법은 $$ {\mathbf{x}}_i^{\mathrm{K}\mathrm{F}}$$, $$ {\mathbf{m}}_i^{\mathrm{K}\mathrm{F}}$$를 기반으로 팩터 그래프(factor graph) 최적화를 통해 수행된다[5]. Fig. 2는 본 논문에서 제안하는 팩터 그래프에 대한 설명이다. 그래프의 첫 번째 노드 x₀는 무인잠수정의 초기 위치 및 자세이며 단항 팩터(unary factor)로 생성한다. 이후에 관성 항법과 MBES로부터 $$ {\mathbf{x}}_i^{\mathrm{K}\mathrm{F}}$$이 생성될 때마다 $$ {\mathbf{x}}_{i-1}^{\mathrm{K}\mathrm{F}}$$에 대한 상대변위 관측값 $$ {\mathbf{z}}_{i-1,i}^{\mathrm{I}\mathrm{N}\mathrm{S}}$$를 계산하고 이에 대한 신뢰도 가중치인 정보행렬 $$ {\mathbf{\Lambda }}_{i-1,i}^{\mathrm{I}\mathrm{N}\mathrm{S}}$$를 추가하여 근접 노드 간의 이항 팩터(binary factor)를 생성한다. 여기까지의 과정은 사실상 그래프를 $$ {\mathbf{x}}_i^{\mathrm{K}\mathrm{F}}$$값으로 초기화하는 것이며 최적화를 진행하더라도 무인잠수정의 위치와 서브맵에 아무 변화는 없다. 최적화 과정에서 변화를 일으키는 중요한 요소는 비근접 노드 간의 이항 팩터이며 이는 폐루프 구속조건(loop closing constraint)이라고도 한다. 본 논문에서는 MBES, USBL로부터 각각 다른 폐루프 구속조건을 생성하는데 지형 기반 항법에서는 MBES에 의한 폐루프 구속조건만 활용한다. MBES 폐루프 구속조건은 새로운 지형 서브맵이 생성될 때마다 기존의 서브맵에 ICP (iterative closest point)[7] 기반의 정합(registration)을 통해 얻는데 이때 정합 연산 효율을 위해 각 서브맵의 도심 C_i와 탐색 반경 R을 사용한다. ICP로부터 계산되는 값은 서브맵 간의 정합 시 발생하는 상대변위 $$ {\mathbf{T}}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}$$이며 이를 현재 서브맵 변위와 함께 이용하면 폐루프 구속조건을 생성할 수 있다. 계산 과정은 아래 식과 같다.

Fig. 2.

Factor graph for UUV localization

$\[ {\mathbf{z}}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}={\left({\mathbf{T}}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}{\mathbf{T}}_i\right)}^{-1}{\mathbf{T}}_j \]$

(2)

여기서 , T_i는 T_j각각 정합이 수행된 두 서브맵의 위치와 자세를 동차 좌표계로 표현한 변환 행렬들이며 $$ {\mathbf{z}}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}$$는 ICP를 통한 상대변위 관측값이다. $$ {\mathbf{z}}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}$$와 이에 대한 정보 행렬 $$ {\mathbf{\Lambda }}_{ij}^{\mathrm{I}\mathrm{C}\mathrm{P}}$$를 이용하여 비근접 노드 간의 이항 팩터를 생성할 수 있다. 일반적으로 연속된 MBES 서브맵 간에는 겹치는 영역이 존재할 수 없기 때문에 ICP를 통해 생성된 구속조건은 항상 폐루프를 생성한다. 비근접 이항 팩터가 추가되면 기존의 모든 팩터와 함께 그래프 최적화를 수행한다. 이를 위해 먼저 잔차(residual)를 아래와 계산한다.

$\[ {\mathbf{r}}_{ij}\left({\mathbf{x}}_{0:N}\right)={\mathbf{z}}_{ij}-h_{ij}\left({\mathbf{x}}_{0:N}\right) \]$

(3)

여기서 N은 현재까지 생성된 키프레임 개수이며 h_ij(x_0:N)는 측정값에 대한 관측모델로 특수 유클리드 군 SE(3) 상에서 , T_i, T_j사이의 상대 변위로 계산된다. 모든 관측값에 대한 잔차가 계산되면 아래 식과 같이 무인잠수정의 최적 경로를 계산한다.

$\[ {\mathbf{x}}_{0:N}^{\mathrm{*}}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{x}}{\mathrm{m}\mathrm{i}\mathrm{n}} \sum {\mathbf{r}}_{ij}{\left({\mathbf{x}}_{0:N}\right)}^{\mathrm{T}}{\mathbf{\Lambda }}_{ij}{\mathbf{r}}_{ij}\left({\mathbf{x}}_{0:N}\right) \]$

(4)

3. 검증용 시뮬레이터 개발

3.1 해양환경 시뮬레이터

제안하는 방법을 검증하기 위해 해양환경 물리엔진이 적용된 시뮬레이터를 개발하였다. 시뮬레이터 구현에는 오픈소스 라이브러리인 Stonefish[8]를 활용하였다. Stonefish는 부력, 드래그, 부가질량과 같은 유체역학 연산을 지원하며 조류, 파고와 같은 환경 외란도 추가할 수 있다. 본 논문에서는 Fig. 3과 같이 시뮬레이터에 무인잠수정과 무인수상선을 각각 1대씩 추가하였으며 연구용 플랫폼으로 많이 활용되고 있는 SPARUSII[9]와 WAMV[10]를 대상 모델로 하였다.

Fig. 3.

(a) UUV and USV in our Stonefish simulator. (b) Sonar sensing simulation.

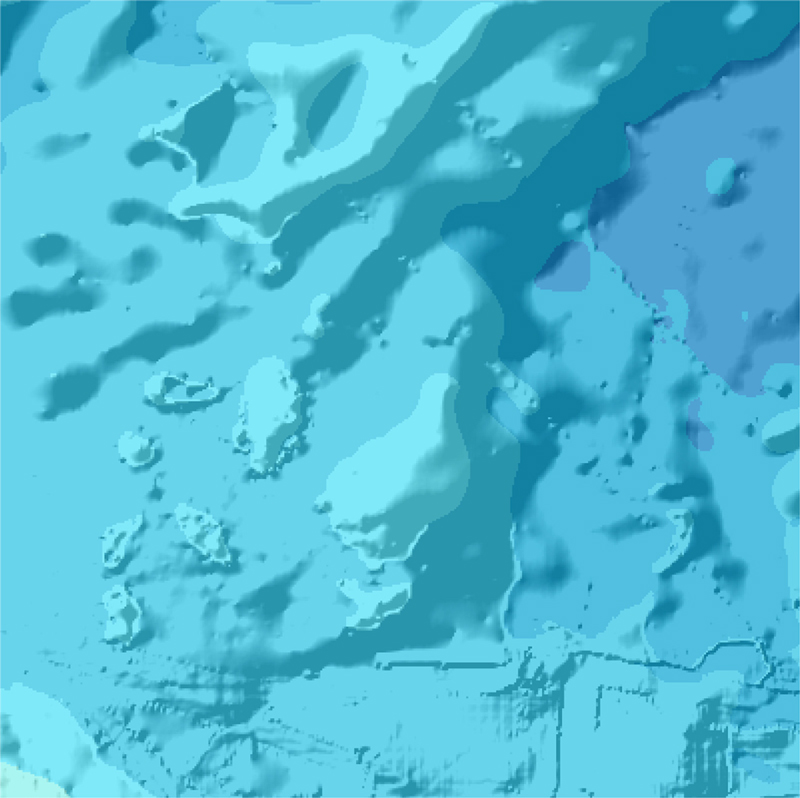
지형 항법을 위해 해저 지형 모델도 시뮬레이터에 추가하였다. 지형 모델은 GEBCO (general bathymetric chart of oceans)[11] 데이터를 활용하여 동해 부근 영역으로 생성하였다. GEBCO 데이터는 실제 해저 지형 대비 해상도가 매우 낮기 때문에(동해 영역의 경우 약 500m) 지형 항법이 제대로 동작할 수 있게 하기 위해 지형 모델 생성 시 매우 큰 영역을 선택한 다음 축소하여 생성하였다. 생성된 지형은 Fig. 4와 같다.

Fig. 4.

Terrain model used in our simulator. East Sea area was cropped from the GEBCO data.

본 논문에서 제안된 항법 알고리즘은 해저 지형 탐사 시나리오를 대상으로 검증하고자 하였으며, 무인잠수정의 탐사 임무 생성에는 오픈소스 소프트웨어인 IquaView를 사용하였다. 임무 정보는 추종 경유점, 유지 심도, 활성화할 페이로드 등이다. 추종 경유점의 경우 잔디깎기(lawn-mower) 패턴으로 하여 MBES 스캔 값이 겹치는 영역이 30% 이상 생기도록 하였는데 이는 서브맵 정합을 하기 위함이며 또한 실제 MBES 값에서 좌우 양단에서 노이즈가 매우 크기 때문에 스캔 양단의 데이터는 일반적으로 사용하지 않기 때문이다. 생성된 임무에 대한 경유점은 Fig. 5와 같다.

Fig. 5.

Mission generation result using IquaView software for SPARUSII survey.

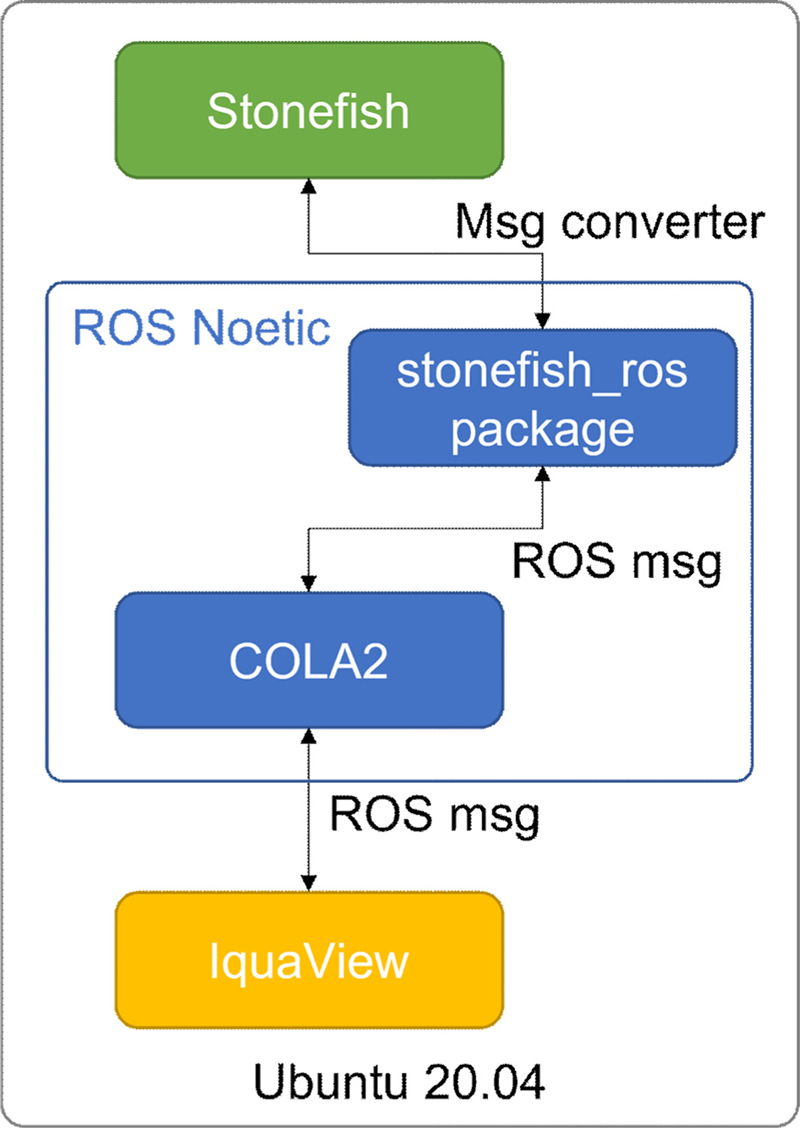
Fig. 6는 소프트웨어 간 메시지 통신 구조를 나타낸다. 항법과 관련한 핵심 소프트웨어 모듈은 ROS (robot operating system)[12]에서 구현되었기 때문에 Stonefish 시뮬레이터와 IquaView로부터 주고받는 모든 정보는 ROS 메시지로 변환되어 사용되었다. 무인수상선과 무인잠수정 간의 통신은 수중음향을 통해 이루어지므로 통신 지연이 불가피하다. 그러나 이 부분은 Stonefish 시뮬레이터 내에서 구현이 되었기 때문에 본 연구에서는 수중음향에서의 통신 지연은 무시하였다. 통신 주기는 1 Hz로 설정하였다.

Fig. 6.

Message interface between core software blocks.

3.2 센서 시스템 구성

무인수상선과 무인잠수정에는 앞서 2장에서 설명한 항법 알고리즘을 수행하기 위한 센서들을 모두 장착하였다. 관성 항법 센서와 USBL 센서는 고가형 일수록 오차가 적고 해상도가 높은데 주로 정밀 탐사나 군용으로 사용된다. 반면 저가형 센서는 연구용 프로토타입 제작, 멀티로봇 시스템 등에 활용될 수 있는 장점이 있다. 때문에 본 논문에서는 항법 시뮬레이션을 저가형과 고가형 센서가 탑재되었을 경우로 나누어서 진행하였다. 이를 위해 시뮬레이션 상에서 센서 정보를 생성할 때 사용되는 파라미터(예: 랜덤 노이즈에 대한 표준오차)들은 저가형과 고가형 상용 제품의 스펙을 반영하여 실제와 유사하도록 하였다. 이렇게 저가형과 고가형으로 나누어 구현한 센서는 AHRS, DVL, USBL이며 구체적인 센서 시뮬레이션 파라미터는 Table 1과 같다. GNSS와 심도계의 경우에는 저가형에서도 충분한 성능을 확보할 수 있기에 동일한 스펙을 사용하였다.

Table 1.

Noise parameters of navigation sensors used in the simulation.*STD: standard deviation

3.3 알고리즘 파라미터 설정

MBES 서브맵 정합에는 PCL (point cloud library)에서 제공하는 GICP (generalized ICP)[7]가 사용되었으며 팩터 그래프 최적화는 g2o 라이브러리[13]를 기반으로 구현되었다. 서브맵 정합과 그래프 최적화 모두 ROS 환경에서 실시간으로 실행되도록 구현되었으며 각각의 알고리즘에서 사용되는 파라미터들은 Table 2와 같다. 이 파라미터들은 알고리즘의 정확도를 높이기 위할 뿐만 아니라 연산의 실시간성을 높이기 위한 값들로 시행 착오를 통해 설정되었다. 표에서 ‘assemble duration’은 서브맵을 생성하는데 필요한 시간 간격이며, ‘info value’는 정보 행렬의 구성요소에 대한 값이다.

Table 2.

Parameters used in the submap registration and graph optimization. Values in parenthesis are used for high-cost sensor scenario.

4. 시뮬레이션 결과

이 장에서는 앞장에서 소개된 해양환경 시뮬레이터 및 임무 계획 소프트웨어, 알고리즘 등을 구동하여 얻게된 데이터를 이용하여 무인잠수정의 탐사 임무 중 위치 추정에 대한 정량적인 성능 평가를 하고자 한다. 첫 번째 성능 지표는 현재까지 추정된 경로에 대해 모든 키프레임의 위치와 레퍼런스 위치와의 유클리디안 거리로 계산되는 절대경로오차(absolute trajectory error, ATE)이며 아래와 같이 계산된다.

여기서 $$ {\mathbf{t}}_i^{\mathrm{K}\mathrm{F}}$$와 $$ {\mathbf{t}}_i^{\mathrm{G}\mathrm{T}}$$는 각각 키프레임과 레퍼런스의 3차원 좌표([x, y, z]^T)이다. 두 번째 성능 지표는 무인잠수정의 이동거리 대비 오차 비율(percent error at distance traveled)로 아래의 식과 같이 계산된다.

관성 항법의 경우 이동 거리가 길어질수록 오차가 크게 누적될 수밖에 없는데 PE는 이동거리와 상관이 없는 지표이므로 서로 다른 주행 거리를 가지는 데이터 셋에 대한 성능 비교 시 ATE보다 적합하다.

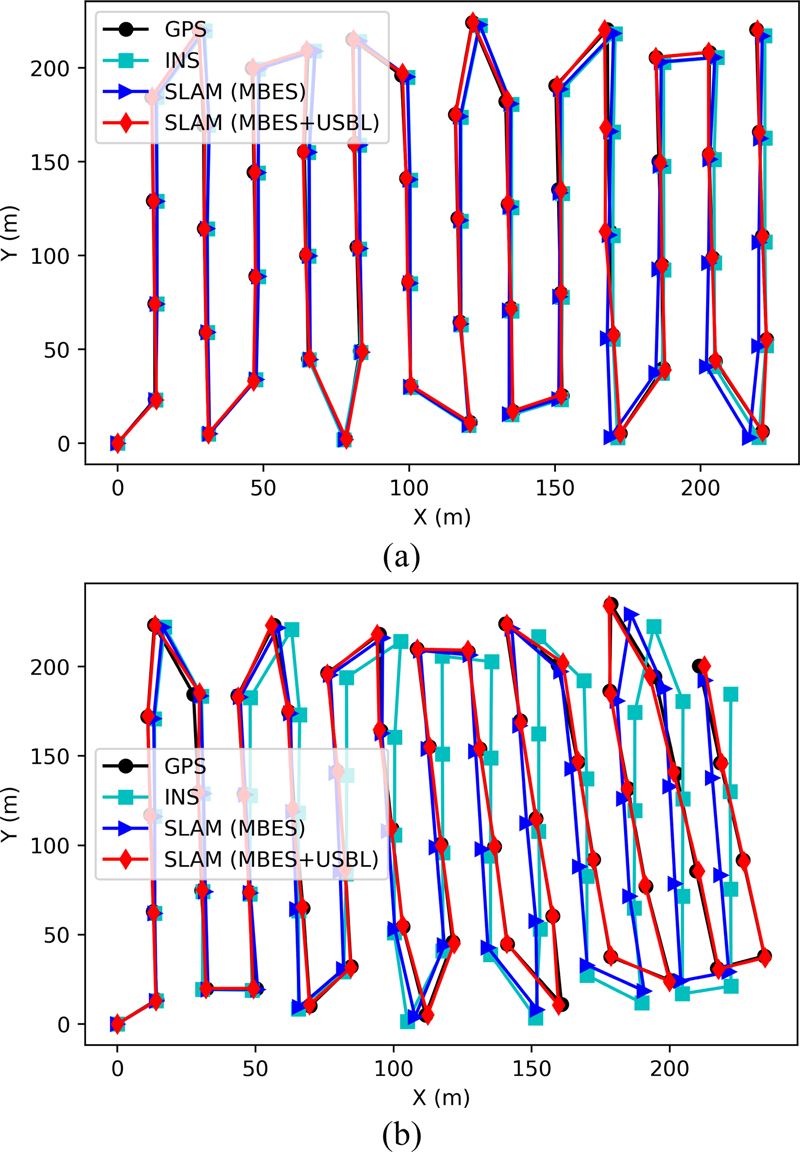
Fig. 7은 센서 성능에 따른 관성 항법 결과를 비교한 것이다. 저가형 센서 사용 시 오차가 두드러지는데 특히 yaw drift에 의한 왜곡이 심한 것을 알 수 있다. 이러한 왜곡을 지형 항법 및 협력 항법을 통해 줄이고자 하는 것이 우리의 목표이다. Fig. 8은 고가형 센서에 대해 협력 항법을 적용한 결과로 추정된 경로 및 지형 정보를 보여준다. 그림에서 빨간색 실선은 폐루프 구속조건인데 지도 원점을 기준으로 생성된 것은 무인수상선의 USBL에 의한 것이며 나머지는 모두 MBES 서브맵 정합에 의한 것이다. 정합 과정은 별도 Fig. 9에 표시하였는데 빨간색 점군이 기존 서브맵, 초록색 점군이 새로 생성된 서브맵, 하늘색 점군이 정합을 통해 이동된 점군이다. 다시 Fig. 8을 보면 키프레임은 원점을 제외하고 총 57개가 생성되었으며, 관성 항법 경로(노락색 실선) 대비 협력 항법 경로(초록색 실선)가 레퍼런스 값(회색 실선)에 근접한 것을 확인할 수 있다. 저가형 센서 및 지형 항법에 대해서도 동일한 시뮬레이션이 수행되었으며 저가형/고가형 센서, 관성 항법/지형 항법/협력 항법 등 모든 조합에 대해 시뮬레이션을 수행하여 추정된 경로는 Fig. 10과 같다. 본 논문에서는 무인잠수정 제어기에 업데이트된 항법 정보를 피드백하지는 않았기 때문에 무인잠수정은 관성 항법을 기준으로 경유점을 추종하였으며 이로 인해 관성 항법 기반 추정 경로는 임무 생성 경로와 가깝게 생성되나 실제 경로는 드리프트가 있는 경로로 나타난다. 이는 Fig. 10 (b)의 저가형 센서 시나리오에서 좀 더 분명하게 확인할 수 있다.

Fig. 7.

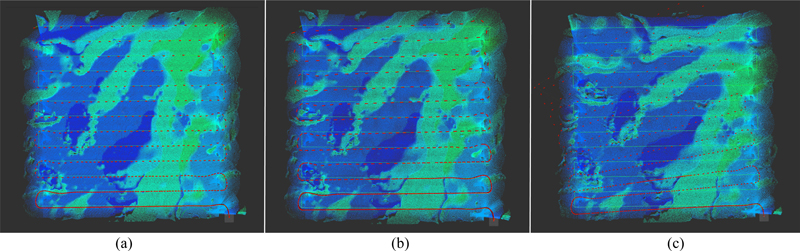
Resulting INS trajectories from the different sensor configurations. (a) Ground truth (no noise). (b) High-cost sensors. (c) Low-cost sensors.

Fig. 8.

Real-time cooperative navigation results. Red lines represent loop closing constraints. Solid lines in other colors represent trajectory of the UUV (yellow: INS, grey: ground truth, green: factor graph SLAM).

Fig. 9.

Example of MBES submap registration using ICP.

Fig. 10.

Comparison of estimated trajectories by (a) high-cost and (b) low-cost sensor scenarios.

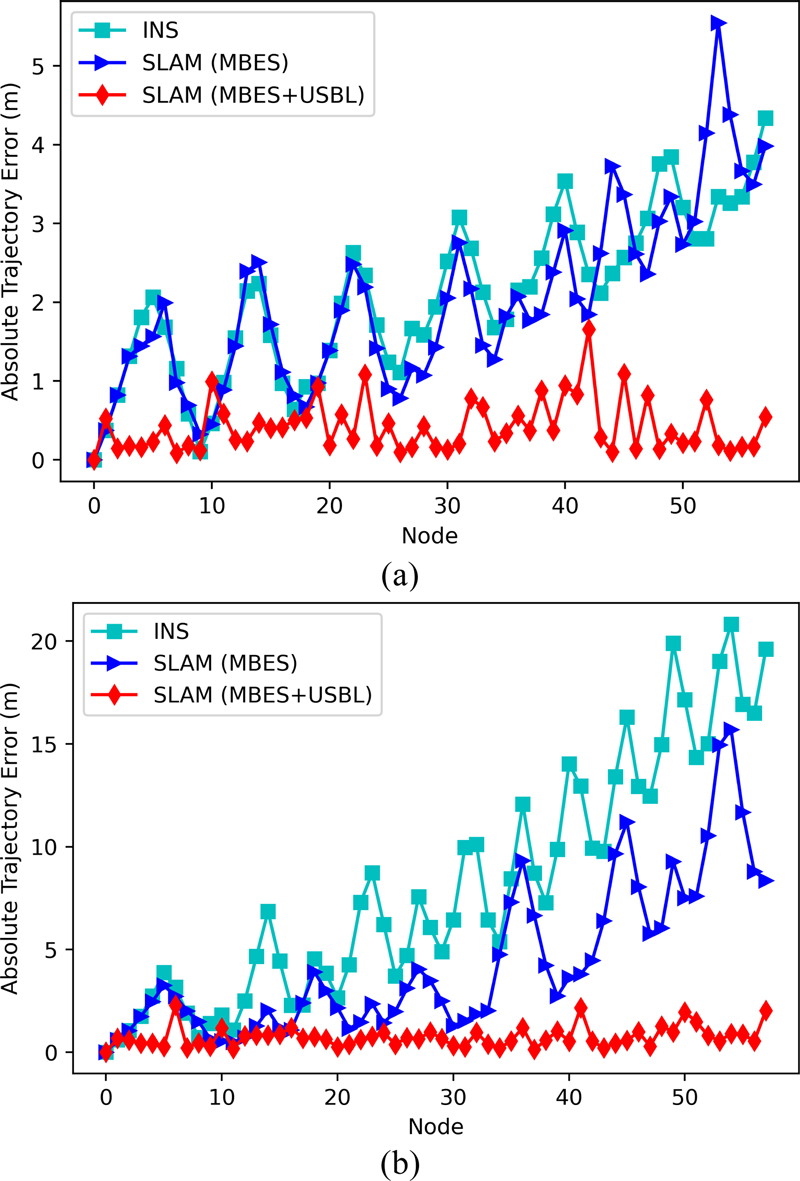
생성된 경로에 대한 추정 성능을 앞서 정의한 정량지표로 평가한 결과는 Figs. 11~12와 같다. ATE의 경우 협력 항법을 제외한 관성 항법과 지형 항법은 저가형 센서와 고가형 센서 시나리오에서 모두 오차가 누적되는 성능을 보였다. 하지만 저가형 센서 시나리오에서는 지형 항법이 관성 항법의 오차 개선에 기여를 하였으나 고가형 센서 시나리오에서는 관성 항법과 성능면에서 큰 차이가 없음을 보였다. 이는 서브맵 정합을 통해 보정되는 변위 값이 작은 것 때문이다. 저가형 센서의 경우 무인잠수정이 새로운 서브맵을 대상으로 정합을 수행할 때 방위 각 드리프트가 많이 쌓여 있는 상태이므로 정합의 효과가 크다. 반면에 고가형 센서는 정합 시점에 쌓인 드리프트가 지형 서브맵 내 변화율과 해상도를 고려했을 때 상대적으로 크지 않기 때문에 정합 효과가 작은 것이다. 협력 항법의 경우 그래프 최적화 과정에서 USBL 팩터가 지배적으로 작용하여 누적오차를 제거하는 결과를 보여주었다.

Fig. 11.

Performance evaluation based on ATE. (a) High-cost and (b) low-cost sensor scenarios.

Fig. 12.

Performance evaluation based on PE. (a) High-cost and (b) low-cost sensor scenarios.

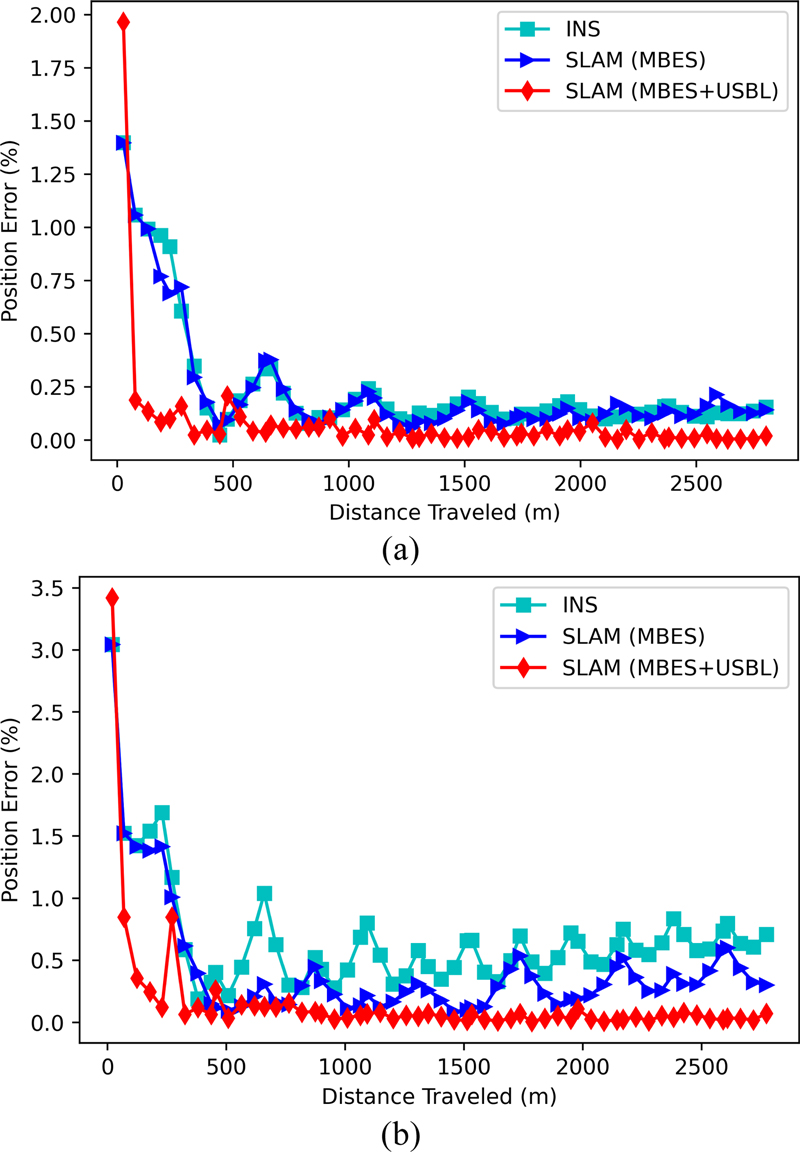
Fig. 12의 거리당 오차율은 약 2.8 km 주행한 것에 대한 결과로 고가형 센서는 관성 항법과 지형 항법 모두 일정한 값을 보여주었다. 반면에 저가형 센서의 경우 거리당 오차율이 선형적으로 증가하는 경향을 보였다. 이는 Fig. 11 (b)에서 ATE 값이 quadratic하게 증가하는 경향을 통해서도 확인할 수 있다.

Table 5는 정량적 성능 지표를 요약한 것이다. 오차율에서 협력 항법은 고가형 센서 시나리오에서 관성 항법 대비 33%, 지형 항법 대비 34% 수준으로 줄었으며 저가형 센서 시나리오에서는 관성 항법 대비 33%, 지형 항법 대비 34% 수준까지 줄일 수 있었다.

Table 5.

Performance evaluation of different navigation systems.

5. 결 론

본 논문에서는 무인잠수정의 관성 항법 기반 위치 인식 성능을 개선하기 위해 MBSE로 획득되는 수중 지형 정보 및 무인잠수정을 추종하는 무인수상선에 장착한 USBL 정보를 활용하는 방법을 제안하였다. 제안된 항법 시스템은 팩터 그래프 최적화 기반으로 설계되었으며 실시간으로 구동될 수 있도록 개발되었다. 제안된 방법의 성능 검증을 위해 해양환경 물리엔진이 적용된 시뮬레이터에서 무인잠수정과 무인수상선을 구현하였으며 저가형 센서와 고가형 센서가 탑재된 시나리오에 대해 탐사 임무를 생성하고 수행하였다. 성능 평가 결과 협력 항법이 기존의 관성 항법과 지형 항법 대비 경로 오차와 오차 누적율에서 큰 개선을 줄 수 있음을 확인하였다. 향후 연구로는 무인수상정이 무인잠수정 추종하는 데 있어 에너지 소비를 최소화하는 유도 및 경로 계획에 대한 연구, 실해역 환경에서 협력 항법에 대한 실험 및 성능 검증 등을 수행할 예정이다.

Acknowledgments

본 연구는 선박해양플랜트연구소의 기본사업인 “다개체 해양로봇의 협력 항법 및 수중 무선 인지 네트워크 핵심 기술 개발”(PES5180)과 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0017006, 2024년 산업혁신인재성장지원사업).

References

• L. Paull, S. Saeedi, M. Seto, and H. Li, “AUV Navigation and Localization: A Review”, IEEE J. Oceanic Eng., Vol. 39, No. 1, pp. 131-149, 2014. [https://doi.org/10.1109/JOE.2013.2278891]
• J. Jung, J. Park, J. Choi, and H.-T. Choi, “Bathymetric Pose Graph Optimization with Regularized Submap Matching”, IEEE Access, Vol. 10, pp. 31155-31164, 2022. [https://doi.org/10.1109/ACCESS.2022.3160190]
• Y. Ling, Y. Li, T. Ma, Z. Cong, S. Xu, and Z. Li, “Active Bathymetric SLAM for Autonomous Underwater Exploration”, Appl. Ocean Res., Vol. 130, p. 103439, 2023. [https://doi.org/10.1016/j.apor.2022.103439]
• S. Thrun, W. Burgard, and D. Fox, Probabilistic Robotics, The MIT Press, Cambridge, MA, pp. 1-647, 2005.
• J. A. Fernández-Madrigal and J. L. B. Claraco, Eds., Simultaneous Localization and Mapping for Mobile Robots: Introduction and Methods, IGI global, Hershey, pp. 1-483, 2012. [https://doi.org/10.4018/978-1-4666-2104-6]
• N. Palomeras, A. Carrera, N. Hurtos, G. Karras, C. Bechlioulis, M. Cashmore, D. Magazzeni, D. Long, M. Fox, K. Kyriakopoulos, P. Kormushev, J. Salvi, and M. Carreras, “Toward Persistent Autonomous Intervention in a Subsea Panel”, Auton. Rob., Vol. 40, pp. 1279-1306, 2016. [https://doi.org/10.1007/s10514-015-9511-7]
• A. Segal, D. Haehnel, and S. Thrun, “Generalized-ICP”, Robotics Sci. Syst., Vol. 2, No. 4, p. 435, 2009. [https://doi.org/10.15607/RSS.2009.V.021]
• P. Cieślak, “Stonefish: An Advanced Open-Source Simulation Tool Designed for Marine Robotics, With a ROS Interface”, Proc. of OCEANS 2019 - Marseille, pp. 1-6, Marseille, France, 2019. [https://doi.org/10.1109/OCEANSE.2019.8867434]
• M. Carreras, J. D. Hernández, E. Vidal, N. Palomeras, D. Ribas, and P. Ridao, “Sparus II AUV—A Hovering Vehicle for Seabed Inspection”, IEEE J. Oceanic Eng., Vol. 43, No. 2, pp. 344-355, 2018. [https://doi.org/10.1109/JOE.2018.2792278]
• J. Pandey and K. Hasegawa, “Study on manoeuverability and control of an autonomous Wave Adaptive Modular Vessel (WAM-V) for ocean observation”, Proc. of 2015 International Association of Institutes of Navigation World Congress (IAIN), pp. 1-7, Prague, Czech Republic, 2015. [https://doi.org/10.1109/IAIN.2015.7352248]
• https://www.gebco.net/, (retrieved on Aug. 26, 2024)
• https://www.ros.org/, (retrieved on Aug. 26, 2024)
• R. Kümmerle, G. Grisetti, H. Strasdat, K. Konolige, and W. Burgard, “g2o: A general framework for graph optimization”, Proc. of IEEE Int. Conf. Robot. Autom., pp. 3607-3613, Shanghai, China, 2011.