Enhanced Fiber Bragg Grating Strain Sensors for Smart Factory Applications: Performance Evaluation
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A fiber Bragg grating (FBG) is an optical device that reflects light within a specific wavelength while allowing others to pass through; this is owing to the periodic variations in the refractive index of the fiber core. Strain sensors based on FBGs are becoming an essential part of smart factory environments because they allow real-time monitoring and optimization of industrial processes. In this study, we designed and analyzed the performance of FBG sensors for sensitive and real-time monitoring of mechanical strain. With an emphasis on strain-induced Bragg-wavelength shifts, this study investigated the basic concepts of FBG strain sensing. Furthermore, the paper discusses the design parameters that can be tuned to improve the accuracy and reliability of the proposed sensor in demanding industrial settings. With a figure of merit of 1.13 × 10-3 με-1, a full width at half maximum of 7.66 nm, a sensitivity of 0.0083 nm/με, and a quality factor of 203.32, the proposed FBG-based strain sensor shows an improved functionality, which may find value in industrial internet of things applications (as in smart factories), particularly in challenging strain settings.
Keywords:
FDTD, Fiber Bragg grating, Strain, Sensitivity, Industrial internet of things, Sustainable development1. INTRODUCTION
Sensor systems and communications were both completely transformed by the discovery of photosensitivity in optical fibers [1-3]. When doped glass (usually silica fibers doped with germanium) is exposed to ultraviolet (UV) radiation, precise modification of the refractive index is feasible [4]. UV exposure is used to periodically vary the refractive index of fiber Bragg gratings (FBGs) along the fiber core, and their photosensitivity is crucial. Frequency bandgaps can be used for wavelength filtering in communication systems and also as strain, temperature, and pressure sensors [5]. These techniques can be combined to form a grating that reflects specific wavelengths of light while allowing others to pass through [5].
Owing to their versatility in serving a wide range of wavelength-selective applications, FBGs have attracted considerable attention recently. The adaptability of these optical devices is well-known in multiple fields [6,7]. FBGs have proven essential in wavelength-selective devices such as filters for wavelength-division multiplexing (WDM) systems and in applications such as dispersion compensation. They are essential for regulating bandwidth and improving signal quality in fiber-optic networks [8]. FBGs also play a significant role as wavelength reflectors in fiber lasers by controlling and stabilizing the output wavelength of the laser. Therefore, they are beneficial in various laser technologies, such as those utilized in precision instruments and medical equipment [8].
1.1 FBG Strain-Sensor Significance for Smart Factory Integration
In smart factories, FBG strain sensors provide a reliable and effective means of real-time monitoring of structural health and precise control of industrial processes [9]. FBG strain sensors are ideal for tracking stress levels inside different components, machine performance, and structural deformations because of their high sensitivity to mechanical strain [9]. The correlation between strain and Bragg-wavelength shifts guarantees precise and consistent measurements, crucial for improving the operational effectiveness and quality in smart factories.
Multiplexing FBG strain sensors with a single optical fiber is a simple process that enables the monitoring of many sites with less complicated infrastructure [10]. This lowers the installation cost and makes it easier to integrate massive sensing networks into a smart factory environment where hundreds of sensing stations are required. Because FBG strain sensors are based on optical fibers, they are highly durable, immune to electromagnetic interference, and resistant to corrosion making them ideal for use in challenging industrial settings. Their usefulness in smart manufacturing is further enhanced by their capacity to function in high-temperature and high-vibration environments.
Process optimization, early defect identification, and predictive maintenance are made possible by real-time data provided by FBG strain sensors. This is in line with the objectives of Industry 4.0, in which sophisticated sensor technology is used by smart factories to reduce downtime, boost output, and guarantee operational safety. Real-time data plays a critical role in the predictive maintenance of smart industries, enabling the replacement or repair of equipment before it breaks down [11]. FBG strain sensors provide real-time monitoring data that can be included in predictive analytical models to guarantee peak performance and minimize expensive downtime.
FBG strain sensors are easily integrated with control systems and machine learning algorithms. As smart industries adopt more automated and intelligent technologies, this enables automatic reactions and sophisticated diagnostics for enhancing decision-making procedures and general efficiency [11,12]. FBG strain sensors are critical to smart industries because they provide: scalability with multiplexing; real-time data necessary for automated operations and predictive maintenance; offer high-precision monitoring; and are robust in harsh environments. Owing to easy integration, which improves operational effectiveness and safety, FBG sensors are an essential part of Industry 4.0.
2. FUNDAMENTALS OF FBG STRAIN SENSORS
Fundamentally, the wavelength shift of a perturbed Bragg signal of an FBG-based sensor is a function of temperature, force, and strain. The refractive index and grating pitch are important factors [13]. These gratings selectively absorb light of Bragg wavelength.
Fracture-band graphene generators rely on the theory of diffraction gratings because their longitudinal refractive indices are periodically regulated. The refractive index of the core is assumed to vary regularly in accordance with the grating [14,15]. The grating reflects a certain wavelength of incident light, from each grating layer, as it passes through an optical fiber sensor. According to the Bragg's equation, the Bragg wavelength (λB) with the highest reflectivity is
| (1.1) |
where neff is the effective refractive index of the fiber, λB is the Bragg wavelength, which corresponds to the wavelength of light reflected by the FBG, and Λ is the periodicity of the grating [15]. When the FBG is subjected to a physical parameter, such as strain or temperature, the effective refractive index and periodicity of the grating change, causing the reflected wavelength to vary, as shown in Fig. 1.
The shift in the Bragg-grating wavelength can be calculated by expanding Eq. (1) in terms of the partial derivatives with respect to the variable length, temperature, and wavelength.
| (1.2) |
In the Bragg grating, strain has two distinct effects.
When the physical distance between successive index modulations changes, there is a shift in the Bragg wavelength [15,16].
The strain-optic effect causes another shift in the Bragg wavelength through a change in the refractive index [17]. The change in the effective refractive index of an optical fiber as a result of mechanical deformation caused by strain or stress, is known as the strain-optic effect [18].
The center wavelength of the Bragg grating varies as a function of strain as follows:
| (1.3) |
Assuming and substituting in Eq. (1.3),
| (1.4) |
The strain-optic or photoelastic coefficients of the material, which relate the changes in the refractive index of the fiber to the applied strain, explain this result.
| (1.5) |
where Sj is the strain vector and pij is the strain-optic tensor in Eq. (1.5) [8]. For the longitudinal strain along the fiber grating axis (z-axis), the strain vector Sj is given by [18,19].
| (1.6) |
where εz denotes strain in the z-direction and v is Poisson’s ratio. There are only two numerical values of pij for a standard germanium-silicate optical-fiber Bragg-grating strain sensor: p11 and p12 [8]. Eq. (1.5) therefore leads to Eq. (1.7):
| (1.7) |
Moreover, since Eq. (1.4) leads to Eq. (1.8).
| (1.8) |
The strain-optic effect can be used to determine the amount of strain an FBG experiences in terms of the differential shift in the Bragg wavelength, as given in Eq. (1.9) [19]. The Bragg wavelength shifts when strain is applied to the optical fiber because it affects both the grating period and effective refractive index.
| (1.9) |
The sum of the strain-induced modifications to the refractive index and the fiber shape is referred to as the index-weighted effective strain-optic coefficient, or peff. It explains how the effective refractive index of the optical fiber is affected by the strain-optic effect when strain is applied and is given by Eq. (2.0).
| (2.0) |
The strain-optic coefficients and Poisson's ratio for a standard silicate optical-fiber Bragg-grating strain sensor are as follows: p11 = 0.113, p12 = 0.252, v = 0.16 respectively [8].
2.1. Design and Simulation of FBG Strain Sensors for Smart Factory Applications
FBGs are extremely sensitive optical sensors and are widely used in many industrial applications to measure strain and temperature.
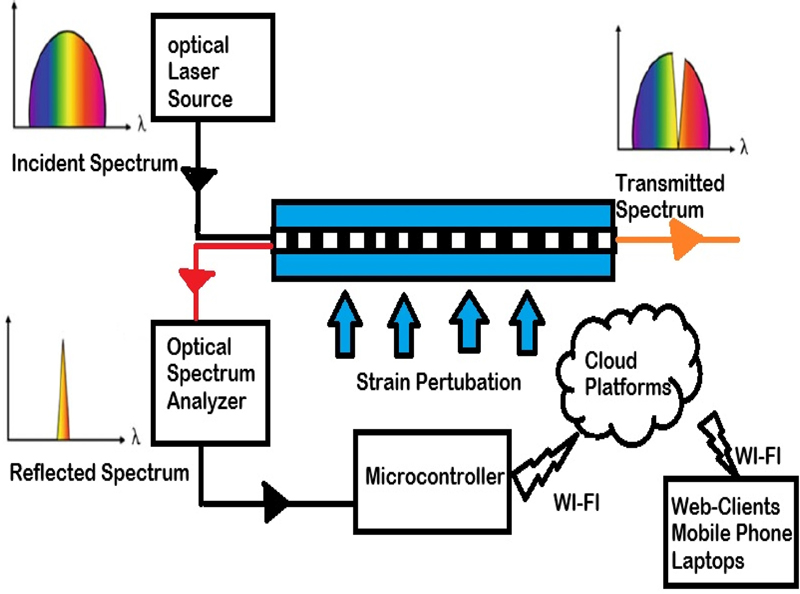
We present the design and modeling of an FBG strain sensor using Lumerical Finite-Difference Time-Domain (FDTD) software [15,20]. This study aimed to assess the sensor performance under various strain conditions to shed light on sensor accuracy and sensitivity in smart-factory applications. Understanding the transmission characteristics requires the ability to capture intricate, time-dependent, electromagnetic-field interactions within the sensor, and FDTD modeling is well suited for this. Therefore, this study used FDTD, a technique that can record transmission, reflections, and transient effects, all of which are important for sensors subjected to fluctuating light or electromagnetic conditions in smart factories. The transmission and reflection properties of the FBG strain sensors could be understood using FDTD simulators [21].
The simulation wavelength was 1.52–1.58 μm, and auto nonuniform mesh resolution was used. To prevent back reflection into the active region, the outgoing waves were absorbed by a perfectly-matched-layer (PML) barrier.
Germanium-doped, silica-fiber-core, Bragg-grating materials, are suited for smart-manufacturing conditions and appropriate for industrial applications; they were used to determine the refractive indices. These selections influence the manner of light–material interactions and are important if a factory has installed optical sensors or imaging equipment [15]. Grating length is important for optical processing and sensing because it determines the diffraction efficiency. In smart factories, grating lengths are tuned to increase the accuracy of data capture, especially in areas such as quality control and product monitoring [20]; sensor outputs with desired sensitivity and quality factors can be achieved by adjusting these lengths. The key design and simulation parameters for the FBG sensor are summarized in Table 1, which also lists the variables affecting strain sensitivity in smart-factory applications.
3. RESULTS AND DISCUSSIONS
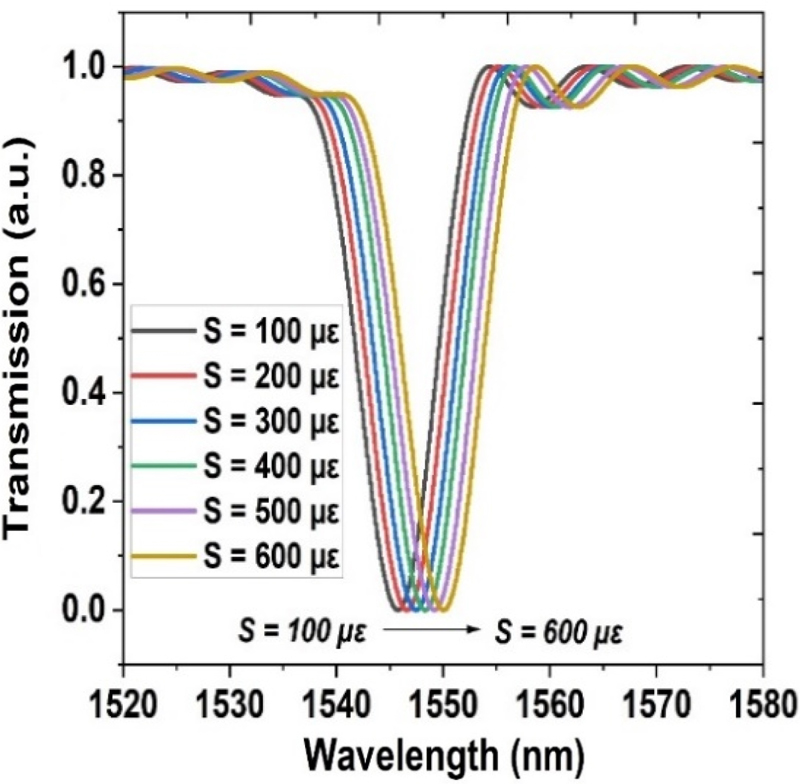
We examined the strain-detection capabilities of the suggested FBG strain-sensor structure, based on the transmission spectrum acquired. Fig. 2 shows the transmission spectrum that indicates the reaction of the FBG strain sensor to varying strain levels. The output-transmission properties of the FBG strain sensor were assessed through a strain range of 100–600 με, with an incremental step of 100 με, using the three-dimensional (3D) FDTD simulation method; this range includes the common strain levels found in real-world settings, such as mechanical-stress assessments, structural-health monitoring, and typical smart factories. As the strain increases, the transmission spectrum clearly demonstrates variations in the Bragg wavelength. These shifts demonstrate how well the suggested design detects strain fluctuations over a given range, confirming the sensitivity of the sensor and the linearity of its reaction to the applied strain.
To guarantee that the proposed FBG-sensor design functions effectively within this strain range, the 3D FDTD approach offers precise modeling of the interaction between light and the grating structure. By examining the transmission spectrum using 100 με increments, we could determine that the sensor responds consistently, which qualifies it for use in real-world strain-sensing applications in smart factories.
The spectral width of an FBG sensor is characterized by the FWHM, which is an important sensor metric [22,23]. For FBG strain sensors, the FWHM aids in determining the sensor bandwidth, which is essential for comprehending the system sensitivity and resolution. The breadth of the spectrum at half of its peak reflectance is the FWHM. The sensor was more accurate in identifying minute variations in the wavelength caused by strain when the FWHM was smaller. The graph in Fig. 2 shows a peak at the Bragg wavelength (the wavelength that the sensor reflects most strongly). The width of this peak at half its maximum height is also known as the FWHM. A narrow peak indicates a smaller FWHM and higher precision, whereas a wider peak indicates a larger FWHM and lower measurement precision.
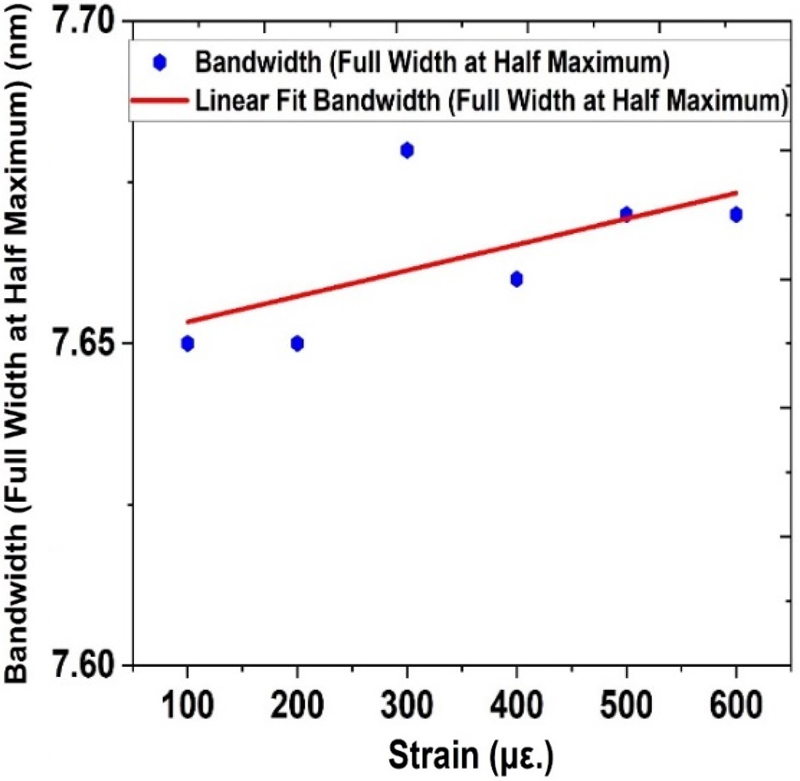
In certain situations, as seen in Fig. 3, in addition to the FWHM, strain also results in Bragg-wavelength changes (depending on the material and structural characteristics of the fiber). The FWHM often widens if the grating is distorted under stress and remains unchanged if the grating remains undistorted. Fig. 3 shows the relationship between the FWHM and the strain in an FBG strain sensor (strain on the x-axis and FWHM bandwidth on the y-axis). The FWHM values are 7.65 nm at 100 με and 7.67 nm at 600 με of strain which is a small variation. The bandwidth is greater under higher strain, and the increase in FWHM with strain is slow. The best-fit curve is shown in Fig. 3, and indicates a linear connection where the FWHM broadens at higher strain values. This pattern suggests that when the strain on the fiber increases, the grating deforms and the FWHM increases slightly the slightness of the increase potentially ensures the stability of the FBG strain sensor, even at high strain.
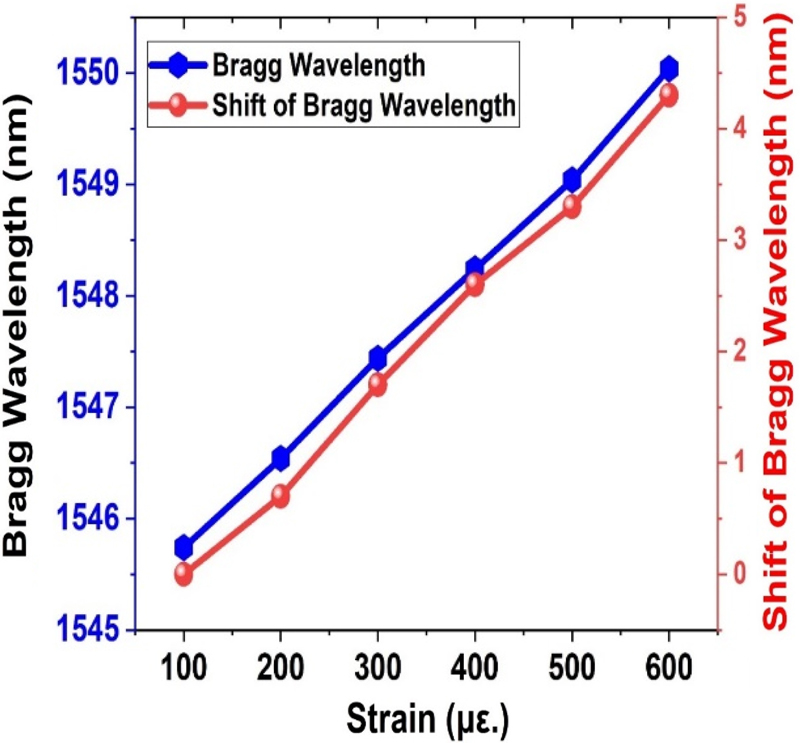
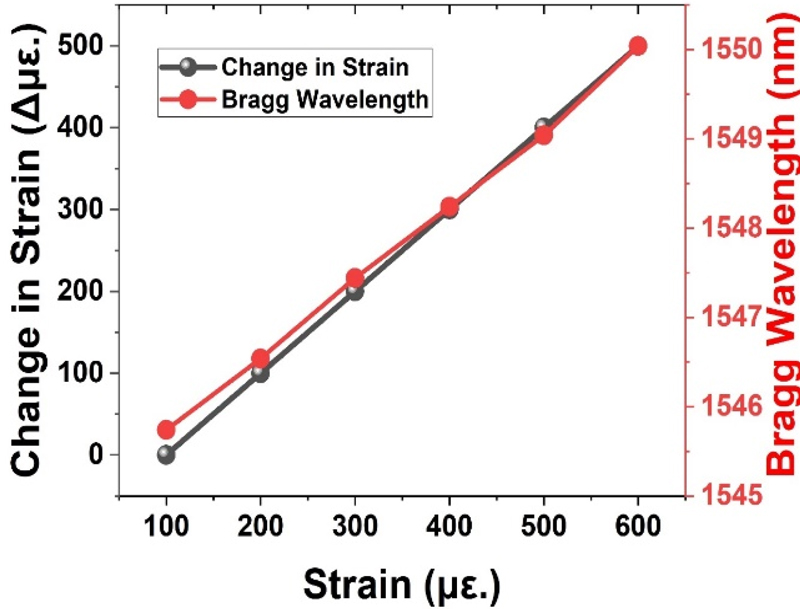
For an FBG sensor, the Bragg-Wavelength shift vs. applied strain graph is approximately linear as seen in Fig. 4. The applied strain, expressed in microstrain (με), is represented on the x-axis in Fig. 4 and ranges from 100–600 με. The Bragg-wavelength shift, or ΔλB (nm), is represented on the y-axis. The Bragg wavelength increases linearly with the strain applied on an FBG. Generally, the Bragg wavelength vs. strain graph shows a linear relationship between the Bragg wavelength and the applied strain on an FBG.
We note that this study, we primarily focused on the effect of strain and assumed a constant temperature. We assumed that the accuracy of the strain measurements would not be significantly impacted by temperature variations in the sensing environment of smart factories and have little to no effect on the Bragg-wavelength shift.
(For specific temperature correction, some setups use a temperature sensor or an additional FBG [15]. With the second sensor supplying the required temperature information to correct the strain measurements, the primary FBG sensor can concentrate exclusively on strain.)
The relationship between the Bragg wavelength and the strain is essentially linear (Fig. 4), and the slope reflects the sensitivity of the fiber sensor. The x-axis represents the strain, and the y-axis represents the Bragg wavelength and change in strain, respectively. Strain results in fiber elongation and refractive-index variations resulting in an increase in the Bragg wavelength. The refractive indices were changed by photoelastic action, and the grating period was changed by the strain-induced fiber elongation. The linear relationship between the Bragg wavelength and applied strain is shown in Fig. 5. The Bragg wavelength increased with strain. In FBG sensors, strain is measured by measuring this wavelength shift. Some of the variables that affect the slope of the graph include the fiber characteristics and effective photoelastic constant.
Table 2 shows the FBG strain sensor response to the applied strain; the wavelength of the reflected light at different stain values is provided.
An external force is applied to the fiber results in deformation, which is measured by strain. A shift in the reflected wavelength occurred in the FBG sensors because the grating period changed as the fiber was stretched or compressed. The Bragg-wavelength shift is the variation in the light wavelength that the FBG reflects. Under most circumstances, the wavelength shift and strain exhibit a linear relationship.
Table 2 shows that greater strain results in a more noticeable shift in the Bragg wavelength. The spectrum reflected by the FBG sensor is referred to as its bandwidth. Numerous factors, such as the applied strain and physical characteristics of the grating, affect the bandwidth. The wideband may vary as the strain increases, particularly if nonlinearities become more noticeable at greater strain levels. The bandwidth changes with applied strain at the Bragg wavelength are presented in Table 2. A modest strain only slightly altered the bandwidth, but a larger strain resulted in more significant broadening or narrowing. (This depends on the sensor design.) Based on whether the strain was compressive or tensile, the shift in the Bragg wavelength varies with increase in strain. Owing to this, the sensor can precisely measure the strain in various smart-manufacturing applications. The bandwidth may not vary at all or may only change marginally with strain as shown in Fig. 3.
The FBG bandwidth generally remains fairly constant in the linear strain-response range; however, it could vary at high strain values, particularly when material fatigue or temperature plays a role. A substantial strain can cause a large wavelength shift, which can alter the bandwidth of the reflection spectrum. The reflection spectrum may widen or contract when the FBG strain sensor deforms further based on the homogeneity of the grating and additional environmental factors such as vibration and temperature.
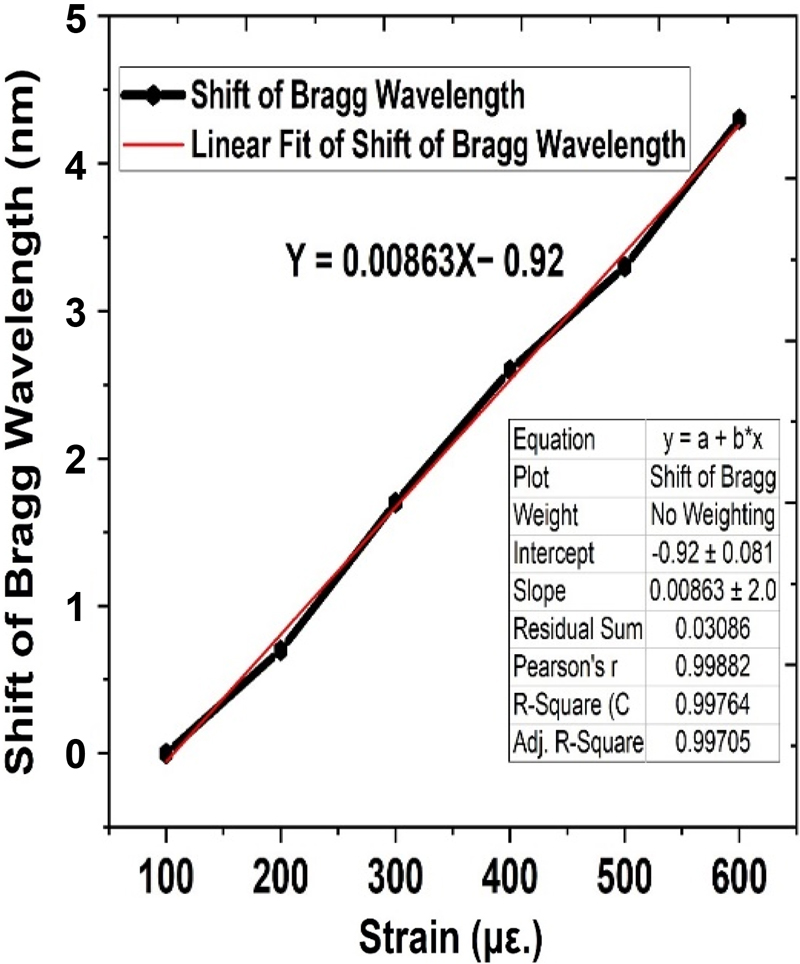
The sensitivity of the FBG sensor is represented by the gradient of the line in the Bragg-wavelength shift vs. strain graph. The Bragg-wavelength shift (nm) per unit of strain (ε) can be used to interpret the sensitivity. From Fig. 6, the FBG strain-sensor sensitivity was calculated as 0.00833 nm/με. That is, the Bragg wavelength shifts by 0.00833 nm for each 1 με of strain given to the sensor.
For smart factory applications such as structural-health monitoring, where regular, dependable strain detection is required, linearity is essential for precise and predictable strain sensing [24-26]. To understand how well an FBG strain sensor reacts to variations in ambient strain, it is imperative to understand the sensitivity of the sensor and its interpretation in IoT smart-industrial applications [24,25].
An increased slope denotes stronger sensitivity to changes in strain. This value represents the resolution of the sensor used to detect the strain. The wavelength at which no strain was applied is indicated by the wavelength-axis intercept. In this instance, the baseline wavelength of the sensor under zero-strain conditions is indicated by the intercept of the graph on the axis at 0.92 nm. This is a critical reference point because it indicates the starting point for detecting wavelength shifts that occur later when strain is applied.
The sensitivity of the FBG sensor is essential for monitoring the structural integrity, equipment health, and overall operational efficiency in the context of IoT applications for smart factories. A sensor sensitivity of 0.00833 nm/με allows it to pick up even minute changes in strain, which makes it a perfect real-time diagnostic tool for situations where accuracy is crucial, such as in smart-industrial settings which require early detection of mechanical failures or deformations. The observed sensor sensitivity of 0.00833 nm/με is consistent with previous research [35-40], suggesting that it functions within anticipated bounds. This compliance attests to the dependability and precision of the sensor when used in IoT-based smart factories.
The lowest detectable wavelength shift is the smallest wavelength change that the sensor can detect.
The ratio of sensor sensitivity to bandwidth or operating range is commonly used to describe the figure of merit (FOM). In this instance, the FOM provides a clear indicator of the sensor performance if the sensitivity of the FBG strain sensor is known and the dynamic range or resolution is considered. The high degree, of sensor precision and suitability (for applications requiring precise strain monitoring, including structural-health monitoring in smart factories [30] or IoT applications), is indicated by its FOM of 1.13 × 10-3 με-1. With such a high FOM value, the sensor is well-suited for applications requiring little signal distortion, high precision, and narrow error margins while operating in complicated situations.
The sensor is perfect for settings in which accuracy is crucial because it can identify even minute variations in strain. This accuracy makes it possible to identify strain-induced wear or damage in industrial machinery early and to prevent breakdowns. In FBG strain sensors, a high signal-to-noise ratio (SNR) is correlated with a high FOM, indicating that the sensor is less vulnerable to noise and external interference. This guarantees measurement accuracy even in difficult or complicated situations, such as those seen in IoT applications or smart factories. Because of this FOM, the FBG strain sensor is a great option for use in IoT smart factories that require high-precision real-time monitoring.
The usefulness of FBG strain sensors in smart industries, transportation infrastructure, and medical equipment is increased by their ability to be integrated into wireless networks and cloud-based platforms for data analysis and decision-making.
In the context of FBG strain sensors, the quality factor (Q-factor) refers to the capacity of the sensor to resonate and retain energy with little loss. This is a crucial metric that establishes the effectiveness and performance of the sensor in identifying and handling strain. With a Q factor of 203.32, the FBG strain sensor exhibits a reasonable amount of energy loss over a prolonged period while maintaining its resonant signal. Consequently, the measurements are more accurate because the sensor is very effective at detecting strains with little signal damping or attenuation.
The resonance bandwidth of the sensor is inversely correlated with the Q-factor. The sensor precisely detected strain-induced wavelength shifts, as indicated by its high Q-factor of 203.32, suggesting a narrow bandwidth. Greater precision and selectivity result from the FBG strain sensor, which responds only to extremely specific wavelengths. With a Q-factor of 203.32, this FBG strain sensor is ideally suited for precision-monitoring applications that require accuracy and dependability in strain detection, such as smart-factory settings, structural health monitoring, and IoT applications. A higher Q-factor also suggests that the sensor is better suited to operate in complicated or loud situations, such as industrial settings, where external influences, such as temperature and vibration, would otherwise affect the operation of lower Q-factor sensors. In summary, an FBG strain sensor with a Q-factor of 203.32 strikes a balance between high sensitivity, narrow bandwidth, and low signal loss, making it an excellent choice for accurate strain detection in applications that require long-term stability and high precision.
Theoretical analysis and large-scale simulations validated the ability of the FBG sensors to measure strain consistently and accurately. Extensive simulations were used to validate the operation of the FBG, demonstrating a linear relationship between the applied strain and Bragg-wavelength shift. This is consistent with the basic idea behind the functioning of FBGs, which states that the strain is directly proportional to the Bragg-wavelength shift. For real-world applications, linearity guarantees that the sensor can accurately map strain-to-wavelength changes, and the exceptional dynamic response of the sensors make them appropriate for industrial settings where real-time monitoring and control are required. This dynamic feature is essential for smart-factory applications, such as structural-health monitoring, aerospace, and civil engineering, where it is important to continuously monitor strain.
Table 3 compares the strain sensitivity of our proposed FBG sensor to that of other strain sensors or materials, with an emphasis on those covered in recent research.

Comparison of the Strain Sensitivity obtained in this study with values obtained in previous studies
The ability of FBG-based sensors to withstand hostile environments is one of their main advantages; this is a crucial prerequisite for Industry 4.0. FBG sensors are used in various industrial settings because of their capacity to withstand mechanical stress [41], operate in high-temperature environments, and resist corrosion. The metrics sensitivity, FWHM, FOM, and Q-Factor are used to efficiently summarize the performance results of our FBG strain sensor in Table 4. Each of these elements is crucial for evaluating the overall performance of the strain sensor.
Additionally, multiplexing allows several FBG sensors to be integrated into a single optical-fiber network, which lowers installation costs and complexity, while offering extensive monitoring throughout large-scale industrial sites [27,30]. This feature is particularly helpful for applications where distributed sensing is crucial, such as predictive maintenance, machinery-condition monitoring, and structural-health monitoring. The temperature sensitivity of FBG strain sensors [28,29], which may affect the measurement accuracy, will be the focus of future research. The dependability and usefulness of FBG strain sensors in Industry 4.0, will be further improved by incorporating temperature-compensation methods and sophisticated data analytics [31-33]. Furthermore, the integration of FBG strain sensors with IoT platforms would enable smooth data gathering, instantaneous processing, and useful insights, propelling further developments in smart manufacturing and must be investigated.
4. CONCLUSION
In Industry 4.0, where precision, robustness, and real-time monitoring are essential, strain sensors based on FBG are particularly effective. According to this study, FBG strain sensors provide several important benefits, such as high sensitivity, immunity to electromagnetic interference, and the capacity to multiplex several sensors with a single optical fiber. These characteristics render FBG strain sensors perfect for the harsh, industrial-automation, and smart-manufacturing settings. The FBG-based strain sensor possesses a high sensitivity of 0.0083 nm/ε, with an FOM of 1.13 × 10-3 ε-1, an FWHM of 7.66 nm and Q of is 203.32. The results confirmed that the FBG strain sensor performed better than before. This enhanced functionality could be useful in Industrial IoT applications, such as smart factories, especially in difficult environments.
Acknowledgments
The researchers would like to express their gratitude to the African Scientific Research and Innovation Council (ASRIC) and the Euro-Mediterranean University of Fes (UEMF) for their financial support in making this research effort feasible.
REFERENCES
-
K. O. Hill, Y. Fujii, D. C. Johnson, and B. S. Kawasaki, “Photosensitivity in optical fiber waveguedes: Application to reflection filter fabrication”, Appl. Phys. Lett., Vol. 32, No. 10, pp. 647-649, 1978.
[https://doi.org/10.1063/1.89881]

-
K. O. Hill, B. Malo, F. Bilodeau, D. C. Johnson, and J. Albert, “Bragg gratings fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask”, Appl. Phys. Lett., Vol. 62, No. 10, pp. 1035-1037, 1993.
[https://doi.org/10.1063/1.108786]

-
C. E. Campanella, A. Cuccovillo, C. Campanella, A. Yurt, and V. M. N. Passaro, “Fibre Bragg grating based strain sensors: Review of technology and applications”, Sensors, Vol. 18, No. 9, p. 3115, 2018.
[https://doi.org/10.3390/s18093115]

-
P. S. Macheso and M. Zekriti, “Reviewing the Role of Fiber Bragg Grating Temperature Sensors in Smart Factories: Opportunities and Challenges”, Proc. of 2022 International Conference on Automation, Computing and Renewable Systems (ICACRS), pp. 45-49, Pudukkottai, India, 2022.
[https://doi.org/10.1109/ICACRS55517.2022.10029317]

-
J. K. Sahota, N. Gupta, and D. Dhawan, “Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review”, Opt. Eng., Vol. 59, No. 6, p. 060901, 2020.
[https://doi.org/10.1117/1.OE.59.6.060901]

-
P. Ferraro and G. De Natale, “On the possible use of optical fiber Bragg gratings as strain sensors for geodynamical monitoring”, Opt. Lasers Eng., Vol. 37, No. 2-3, pp. 115-130, 2002.
[https://doi.org/10.1016/S0143-8166(01)00141-5]

-
S. Daud and J Ali, Fibre Bragg grating and no-core fibre sensors, New York, Springer, NY, pp. 1-81, 2018.
[https://doi.org/10.1007/978-3-319-90463-4_1]

-
H. K. Hisham, Fiber bragg grating sensors: development and applications, Boca Raton, CRC Press, FL, pp. 1-117, 2019.
[https://doi.org/10.1201/9780429275135-1]

-
A. Othonos, K. Kalli, and G. E. Kohnke, “Fiber Bragg gratings: Fundamentals and applications in telecommunications and sensing”, Phys. Today, Vol. 53, No. 5, pp. 61-62, 2000.
[https://doi.org/10.1063/1.883086]

-
L. M. Zhang, Y. He, S. Cheng, H. Sheng, K. Dai, W. J. Zheng, M. X. Wang, Z. S. Chen, Y. M. Chen, and Z. Suo, “Self-healing, adhesive, and highly stretchable ionogel as a strain sensor for extremely large deformation”, Small, Vol. 15, No. 21, p. 1804651, 2019.
[https://doi.org/10.1002/smll.201804651]

-
O. Hill and G. Meltz, “Fiber Bragg grating technology fundamentals and overview”, J. Lightwave Technol., Vol. 15, No. 8, pp. 1263-1276, 1997.
[https://doi.org/10.1109/50.618320]

-
T. S. Hsieh, Y. C. Chen, and C. C. Chiang, “Analysis and Optimization of Thermodiffusion of an FBG Sensor in the Gas Nitriding Process, Micromachines, Vol. 7, No. 12, p. 227, 2016.
[https://doi.org/10.3390/mi7120227]

-
P. M. Ferreira, M. A. Machado, M. S. Carvalho, and C. Vidal, “Embedded sensors for structural health monitoring: Methodologies and applications review”, Sensors, Vol. 22, No. 21, p. 8320, 2022.
[https://doi.org/10.3390/s22218320]

-
P. S. Macheso and M. Zekriti, “Single-Mode versus Multimode Fiber Bragg Grating Temperature Sensors: A Theoretical Study”, Results Opt., Vol. 16, p. 100739, 2024.
[https://doi.org/10.1016/j.rio.2024.100739]

-
P. S. Macheso and M. Zekriti, “Modelling and analysis of fiber Bragg grating temperature sensor for Internet of things applications (FBG-4-IoT)”, Int. J. Intell. Networks, Vol. 5, pp. 224-230, 2024.
[https://doi.org/10.1016/j.ijin.2024.05.006]

-
P. S. B. Macheso, T. D. Manda, A. G. Meela, J. S. Mlatho, G. T. Taulo, and J. C. Phiri, “Industrial Temperature Monitor Based on NodeMCU ESP8266, MQTT and Node-RED”, Proc. of 2021 3rd International Conference on Advances in Computing, Communication Control and Networking (ICAC3N), pp. 740-743, Greater Noida, India, 2021.
[https://doi.org/10.1109/ICAC3N53548.2021.9725469]

-
P. Ferraro and G. De Natale, “On the possible use of optical fiber Bragg gratings as strain sensors for geodynamical monitoring”, Opt. Lasers Eng., Vol. 37, No. 2-3, pp. 115-130, 2002.
[https://doi.org/10.1016/S0143-8166(01)00141-5]

- B. A. Tahir, J. A. Saktioto, M. Fadhali, R. A. Rahman, and A. Ahmed,“A study of FBG sensor and electrical strain gauge for strain measurements”, J. Optoelectron. Adv. Mater., Vol. 10, No. 10, pp. 2564-2568, 2008.
-
B. Torres, I. Pay-Zaforteza, P. A. Calderón, and J. M. Adam, “Analysis of the strain transfer in a new FBG sensor for structural health monitoring”, Eng. Struct., Vol. 33, No. 2, pp. 539-548, 2011.
[https://doi.org/10.1016/j.engstruct.2010.11.012]

-
T. J. Arsenault, A. Achuthan, P. Marzocca, C. Grappasonni, and G. Coppotelli, “Development of a FBG based distributed strain sensor system for wind turbine structural health monitoring”, Smart Mater. Struct., Vol. 22, No. 7, p. 075027, 2013.
[https://doi.org/10.1088/0964-1726/22/7/075027]

-
M. Liu, W. Wang, H. Song, S. Zhou, and W. Zhou, “A high sensitivity FBG strain sensor based on flexible hinge”, Sensors, Vol. 19, No. 8, p. 1931, 2019.
[https://doi.org/10.3390/s19081931]

-
J. Yang, P. Hou, C. Yang, and N. Yang, “Study of a long-gauge FBG strain sensor with enhanced sensitivity and its application in structural monitoring”, Sensors, Vol. 21, No. 10, p. 3492, 2021.
[https://doi.org/10.3390/s21103492]

-
L. Ren, Z. Jia, H. Li, and G. Song, “Design and experimental study on FBG hoop-strain sensor in pipeline monitoring”, Opt. Fiber Technol., Vol. 20, No. 1, pp. 15-23, 2014.
[https://doi.org/10.1016/j.yofte.2013.11.004]

- HBM GmbH, Strain measurement with fiber Bragg grating sensors, HBM GmbH, Darmstadt, 2006.
-
N. Kuse, A. Ozawa, and Y. Kobayashi, “Static FBG strain sensor with high resolution and large dynamic range by dual-comb spectroscopy”, Opt. Express, Vol. 21, No. 9, pp. 11141-11149, 2013.
[https://doi.org/10.1364/OE.21.011141]

-
Y. Hamed, G. O'Donnell, N. Lishchenko, and I. Munina, “Strain Sensing Technology to Enable Next-Generation Industry and Smart Machines for the Factories of the Future: A Review”, IEEE Sens. J., Vol. 23, No. 21, pp. 25618-25649, 2023.
[https://doi.org/10.1109/JSEN.2023.3313013]

-
O. Alruwaili, F. Wu, W. Mobarak, and A. Armghan, “Enhancing Smart Factories Through Intelligent Measurement Devices Altering Smart Factories via IoT Infusion”, IEEE Access, Vol. 12, pp. 45961-45975, 2024.
[https://doi.org/10.1109/ACCESS.2024.3382214]

-
K. M. Sousa, U. J. Dreyer, C. Martelli, and J. C. C. da Silva, “Dynamic eccentricity induced in induction motor detected by optical fiber Bragg grating strain sensors”, IEEE Sens. J., Vol. 16, No. 12, pp. 4786-4792, 2016.
[https://doi.org/10.1109/JSEN.2016.2554885]

-
R. Li, Y. Chen, Y. Tan, Z. Zhou, T. Li, and J. Mao, “Sensitivity enhancement of FBG-based strain sensor”, Sensors, Vol. 18, No. 5, p. 1607, 2018.
[https://doi.org/10.3390/s18051607]

-
E. J. Friebele, “Fiber Bragg grating strain sensors: present and future applications in smart structures”, Opt. Photonics News, Vol. 9, No. 8, p. 33, 1998.
[https://doi.org/10.1364/OPN.9.8.000033]

-
L. Tang, X. Tao, and C. Choy, “Effectiveness and optimization of fiber Bragg grating sensor as embedded strain sensor”, Smart Mater. Struct., Vol. 8, No. 1, p. 154, 1999.
[https://doi.org/10.1088/0964-1726/8/1/017]

-
J. Park, Y. S. Kwon, M. O. Ko, and M. Y. Jeon, “Dynamic fiber Bragg grating strain sensor interrogation with real-time measurement”, Opt. Fiber Technol., Vol. 38, pp. 147-153, 2017.
[https://doi.org/10.1016/j.yofte.2017.09.011]

-
F. Kosova, . Altay, and H. . Ünver, “Structural health monitoring in aviation: a comprehensive review and future directions for machine learning”, Nondestr.Test. Eval., pp. 1-60, 2024.
[https://doi.org/10.1080/10589759.2024.2350575]

-
C. E. Campanella, A. Giorgini, S. Avino, P. Malara, R. Zullo, G. Gagliardi, and P. De Natale, “Localized strain sensing with fiber Bragg-grating ring cavities”, Opt. Express, Vol. 21, No. 24, pp. 29435-29441, 2013.
[https://doi.org/10.1364/OE.21.029435]

-
Y. Zhang and W Yang, “Simultaneous precision measurement of high temperature and large strain based on twisted FBG considering nonlinearity and uncertainty”, Sens. Actuators A Phys., Vol. 239, pp. 185-195, 2016.
[https://doi.org/10.1016/j.sna.2016.01.012]

-
H. Zhang, Q. Wang, H. Wang, S. Song, B. Zhao, Y. Dai, G. Huang, and Z. Jiang, “Fiber Bragg grating sensor for strain sensing in low temperature superconducting magnet”, IEEE Trans. Appl. Supercond., Vol. 20, No. 3, pp. 1798-1801, 2010.
[https://doi.org/10.1109/TASC.2010.2042693]

-
R. Cheng, L. Xia, Y. Ran, J. Rohollahnejad, J. Zhou, and Y. Wen, “Interrogation of ultrashort Bragg grating sensors using shifted optical Gaussian filters”, IEEE Photonics Technol. Lett., Vol. 27, No. 17, pp. 1833-1836, 2015.
[https://doi.org/10.1109/LPT.2015.2443812]

-
Y. W. Wang, Y. Q. Ni, and X. Wang, “Real-time defect detection of high-speed train wheels by using Bayesian forecasting and dynamic model”, Mech. Syst. Signal Process., Vol. 139, p. 106654, 2020.
[https://doi.org/10.1016/j.ymssp.2020.106654]

-
W. Yuan, A. Stefani, and O. Bang, “Tunable polymer fiber Bragg grating (FBG) inscription: fabrication of dual-FBG temperature compensated polymer optical fiber strain sensors”, IEEE Photonics Technol. Lett., Vol. 24, No. 5, pp. 401-403, 2011.
[https://doi.org/10.1109/LPT.2011.2179927]

-
M. S. Ferreira, J. Bierlich, M. Becker, K. Schuster, J. L. Santos, and O. Frazão, “Ultra-high sensitive strain sensor based on post-processed optical fiber Bragg grating”, Fibers, Vol. 2, No. 2, pp. 142-149, 2014.
[https://doi.org/10.3390/fib2020142]

-
A. Theodosiou, “Recent Advances in Fiber Bragg Grating Sensing”, Sensors, Vol. 24, No. 2, p. 532, 2024.
[https://doi.org/10.3390/s24020532]

-
Y. Wang, X. Qiao, H. Yang, D. Su, L. Li, and T. Guo, “Sensitivity-improved strain sensor over a large range of temperatures using an etched and regenerated fiber Bragg grating”, Sensors, Vol. 14, No. 10, pp. 18575-18582, 2014.
[https://doi.org/10.3390/s141018575]

-
K. Bhowmik, G. D. Peng, Y. Luo, E. Ambikairajah, V. Lovric, W. R. Walsh, and G. Rajan, “High intrinsic sensitivity etched polymer fiber Bragg grating pair for simultaneous strain and temperature measurements”, IEEE Sens. J., Vol. 16, No. 8, pp. 2453-2459, 2016.
[https://doi.org/10.1109/JSEN.2016.2519531]

-
C. E. Campanella, “Coupled π-shifted fibre Bragg grating ring resonant strain sensors”, Electron. Lett., Vol. 52, No. 22, pp. 1873-1875, 2016.
[https://doi.org/10.1049/el.2016.2526]

-
L. Zhang, X. Chang, Y. Zhang, and F. Yang, “Large strain detection of SRM composite shell based on fiber Bragg grating sensor”, Photonic Sensors, Vol. 7, No. 4, pp. 350-356, 2017.
[https://doi.org/10.1007/s13320-017-0423-3]

-
T. Yang, X. Qiao, Q. Rong, and W. Bao, “Fiber Bragg gratings inscriptions in multimode fiber using 800 nm femtosecond laser for high-temperature strain measurement”, Opt. Laser Technol., Vol. 93, pp. 138-142, 2017.
[https://doi.org/10.1016/j.optlastec.2017.01.033]

-
H. Xiang and Y. Jiang, “Fiber Bragg grating inscription in multi-core photonic crystal fiber by femtosecond laser”, Optik, Vol. 171, pp. 9-14, 2018.
[https://doi.org/10.1016/j.ijleo.2018.06.020]

-
Y. Liu, X. Song, B. Li, J. Dong, L. Huang, D. Yu, and D. Feng, “Simultaneous measurement of temperature and strain based on SCF-based MZI cascaded with FBG”, Appl. Opt., Vol. 59, No. 30, pp. 9476-9481, 2020.
[https://doi.org/10.1364/AO.405670]