Identifying Puddles based on Intensity Measurement using LiDAR
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(https://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
LiDAR, one of the most important sensing methods used in mobile robots and cars with assistive/autonomous driving functions, is used to locate surrounding obstacles or to build maps. For real-time path generation, the detection of potholes or puddles on the driving surface is crucial. To achieve this, we used the coordinates of the reflection points provided by LiDAR as well as the intensity information to classify water areas, which was achieved by applying a linear regression method to the intensity distribution. The rationale for using the LiDAR index as an input variable for linear regression is presented, and we demonstrated that it is not affected by errors in the distance measurement value. Because of LiDAR vertical scanning, if the reflective surface is not uniform, it is divided into different groups according to the intensity distribution, and a mathematical basis for this is presented. Through experiments in an outdoor driving area, we could distinguish between flat ground, potholes, and puddles, and kinematic analysis was performed to calculate the maximum width that could be crossed for a given vehicle body size and wheel radius.
Keywords:
Puddle, Autonomous vehicle, LiDAR, Linear regression, Data segmentation1. INTRODUCTION
LiDAR is used in various devices such as mobile robots and autonomous cars for obstacle detection, localization, map generation, and simultaneous localization and mapping (SLAM). By measuring the time for laser light to reflect and return, LiDAR can calculate the distance to the reflection point. 3D LiDAR, which measures the omnidirectional range in the horizontal direction and a limited range in the vertical direction at high speeds, has been commercialized and, despite being relatively expensive, has become an essential sensing method. For general road driving, [1] determined the border of a road using LiDAR, and [2] generated road models and maps by fusing inertial navigation devices, GPS information, and LiDAR. Intensity, which is another measurement of LiDAR, is the intensity of the laser reflected from the measurement point, and the reflectivity is determined by the component of the surface from which the light is reflected. LiDAR intensity measurements are used to distinguish soil, tree areas, and river or stream areas using special LiDAR installed on aircraft when creating aerial maps [3,4]. For autonomous driving, [5] described a study to determine paved and unpaved surfaces based on the dispersion value of the intensity of LiDAR laser beams. In [6], the reflectivity according to the distance of a covered road was measured, and a correction equation was derived using the reflectivity of soil, cement, grass, and asphalt. Ref. [7] measured the reflectivity of drivable roads, created a model for the drivable area, and continuously updated it to create a drivability probability map.
For outdoor driving robots, the driving road may contain puddles or potholes even on paved roads. The presence of water affects the reflection of the laser, and the accuracy of the distance measurements decreases owing to diffuse reflection from the water. Therefore, if the presence of water can be determined, the accuracy is expected to decrease. Additionally, detecting water puddles and determining whether they can be passed are essential for creating a real-time path.
In this study, we performed an experiment in an environment with a water reservoir and developed a method for estimating the exact location of a water puddle through changes in LiDAR intensity measurements. Based on the general characteristics of intensity, we propose a group segmentation method that uses the scan order rather than the measurement position of the reflective surface, assuming a change in intensity as a linear model. This was experimentally verified in an outdoor environment comprising puddles, potholes, and flat areas. In addition, geometric analysis was performed to determine the maximum width that a mobile robot can pass through in the presence of puddles or potholes rather than continuous terrain.
2. LiDAR Data Segmentation
2.1 Reading a Water Surface using LiDAR
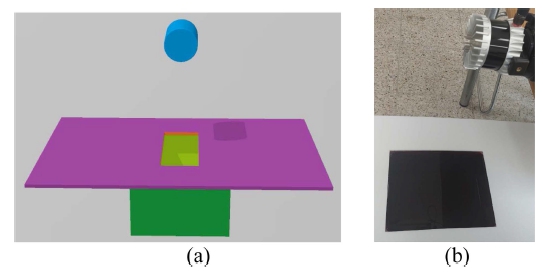
To check the accuracy of the distance measurements using LiDAR when a water puddle exists, we configured an experimental device as shown in Fig. 1. A reservoir filled with water was placed on a floor, a plate with a square hole was placed on top of the reservoir, and a LiDAR sensor was installed pointing towards the center of the water surface. At the center of the water, the angle of incidence of the laser beam was 0°, and the angle of incidence increased in the left and right directions. The change in the accuracy of the measurement value of the angle of incidence was confirmed by moving the position of the water tank
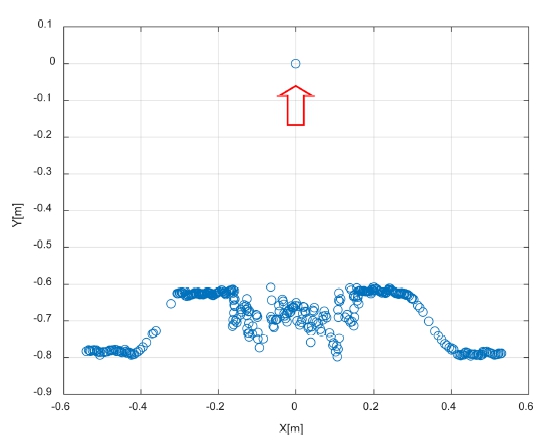
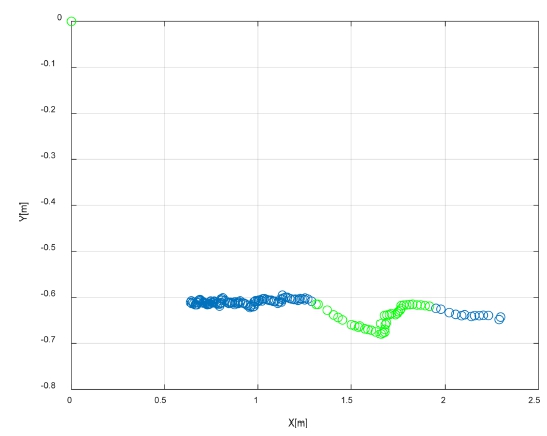
Fig. 2 shows the surface coordinate x, y from LiDAR. The right and top directions are the +X and +Y, respectively. Although the distance from the center to the water was 0.6 m, inaccurate values were output in the water surface area. More importantly, many measurements had an output of 0 because of a failure to measure properly. In this study, the goal was not to accurately measure the distance to the water surface but to recognize the area with water.
3D LiDAR is designed to scan a certain range of vertical and omnidirectional horizontal surfaces. For Ouster OS1 LiDAR, which was used in the experiment, the horizontal plane is scanned with 2048 channels, and the vertical plane is scanned with 128 channels over a 45° range. As shown in Fig. 3, an index was used to distinguish each measurement point; the vertical surface had an output format in which the vertical index j increased from top to bottom, and the horizontal surface had an output format in which the horizontal index i increased clockwise when viewed from above.
In this study, to increase the measurement range and resolution of the vertical plane, we rotated the LiDAR 90° and fixed it, as shown in Fig. 1, and the resolution of the vertical plane was used as 2048 channels. In this paper, the LiDAR index is denoted as i, as shown in Fig. 3. LiDAR measures the distance to the laser beam reflection point (R), and outputs the coordinates of the reflection point (x, y, z) with respect to the LiDAR origin calculated internally using Eq. (1).
| (1) |
The computation time is reduced and the sampling frequency is increased by storing the values of cosθcosψ, cosθsinψ, sinθ for each scan position in advance as constant values, and the coordinate values are output by multiplying them with the measured distance value R. If the distance value is 0 owing to a measurement error, all the coordinates of the reflection point are output as 0. Although such errors rarely occur during LiDAR scanning, we confirmed that many errors occur when scanning the water surface. Therefore, the coordinate values may include significant amounts of errors; therefore, the intensity information is expressed based on the index value of the LiDAR instead, as shown in Fig. 4. In the figure, when the index value is 1024, the laser ray hits the center of the water surface. The intensity is relatively small in the area with water, and differences are observed in the plate part above the water tank located on the left and right sides and in the floor part on both sides. This paper presents a method for differentiating laser reflection surfaces using intensity information.
2.2 LiDAR Intensity Output Segmentation
The basic principle of LiDAR, which measures the distance to a reflection point, involves calculating the distance from the time required for the laser light to reflect and return. LiDAR provides not only the coordinates for each measurement point but also information such as intensity and reflectivity.
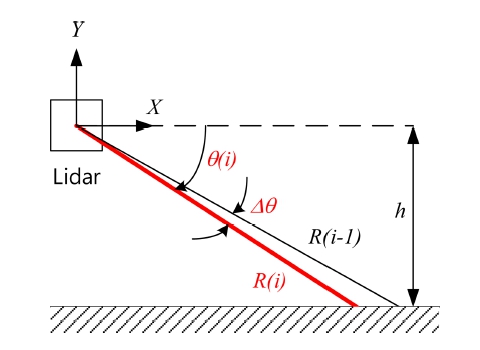
Fig. 5 shows the parameters associated with LiDAR installed at a height of h above the ground.
The index value increases from top to bottom when scanning the vertical plane, and this is the movement position of the LiDAR internal mechanism, which can be assumed to be accurate. The angle changes for each index are set as equal; therefore, the value of ∆θ in the figure is constant. The distance from the LiDAR origin corresponding to index i to the measurement point has the following relationship:
| (2) |
The intensity is affected by the ambient lighting, reflector material, angle of incidence, and distance. For a surface with the same reflectivity, the intensity of the light reflected by the laser beam is inversely proportional to the square of the distance.
| (3) |
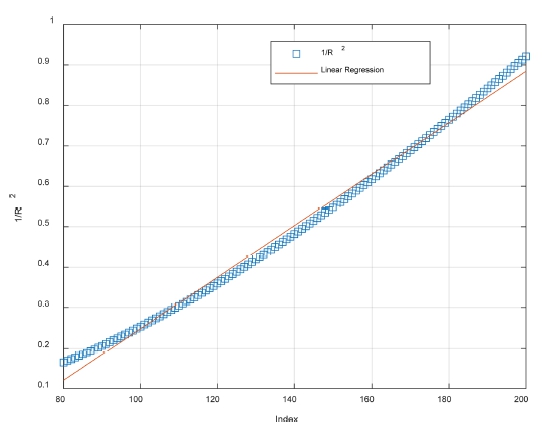
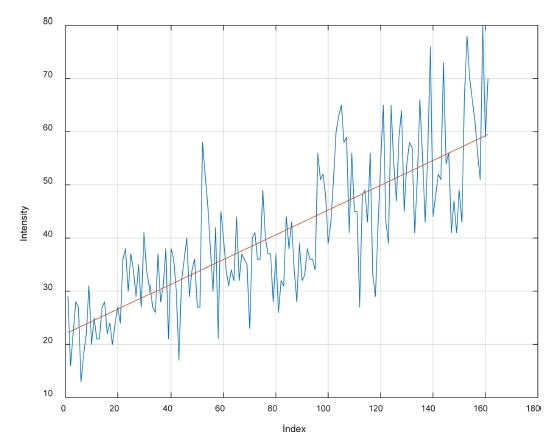
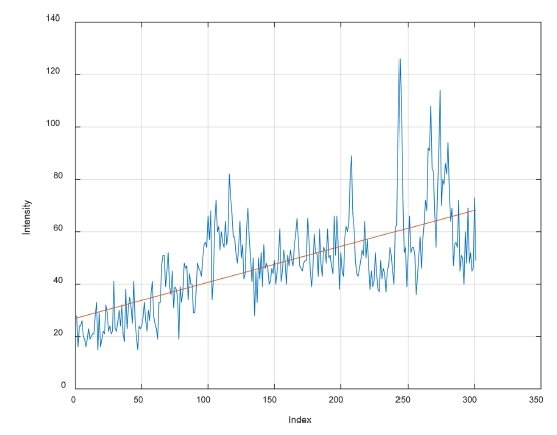
For the main area of interest, which is the lower half of the front when the LiDAR is installed at the height h = 0.8m, the relationship between the index value and the inverse squared distance is shown in Fig. 6. We can reasonably assume that , shown in blue, has a linear relationship with index i. The red line in the figure represents a linear relationship with the index.
Because the intensity is proportional to , and has a linear relationship with i, the intensity is assumed to have a linear relationship with i for the same reflector material, and the measured intensity is analyzed using the linear regression method.
In the linear regression method, the relationship between the input variable xi = 1,...,N and output variable yi = 1,...,N is expressed in the form of Eq. (4), where is the output value obtained using the linearized equation.
| (4) |
The parameters a, b are obtained by the following minimization method.
| (5) |
Using the expressions defined in Eqs. (6)-(8),
| (6) |
| (7) |
| (8) |
where , in Eq. (4) can be obtained using Eq. (9) and Eq. (10), respectively:
| (9) |
| (10) |
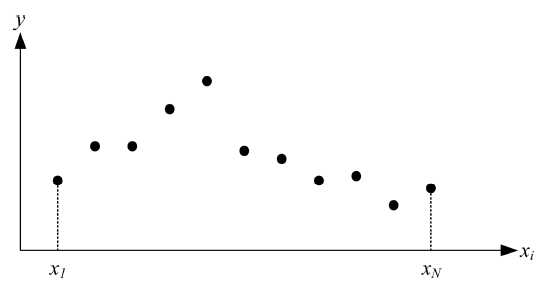
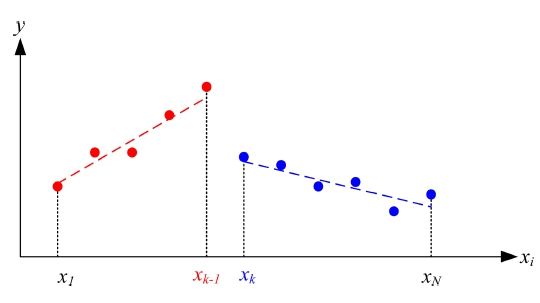
To explain the concept of group segmentation, if the distribution of x, y consisting of two groups with a linear relationship is shown in Fig. 7.
The method of segmenting data into two groups involves finding values that classify one group of ranges i = 1, ⋯ , k-1 and the other group of ranges i = k, ..., N, which is an optimization that minimizes the objective function in Eq. (11).
| (11) |
where, is the output calculated using the equation after linearizing the group consisting of i = 1, ⋯ ,k-1 and corresponds to the group consisting of i = k, ⋯ , N. The expected optimization results are shown in Fig. 8. The dotted lines represent linear equations for each group.
To improve the speed of the optimization process, we use the relationship in Eq. (12) to calculate Eq. (11).
| (12) |
Because the number of groups cannot be specified in advance for the measured values of the area of interest, the number of groups is also determined in the optimization process. This method is based on the residual error (sum of squares error) of the entire dataset. For example, if the residual error divided into two groups is smaller than the residual error when expressed as a single group using a linear regression equation, it is divided into two groups. However, as the number of groups increases, the residual error naturally decreases. Thus, a penalty that increases linearly with the number of groups is used.
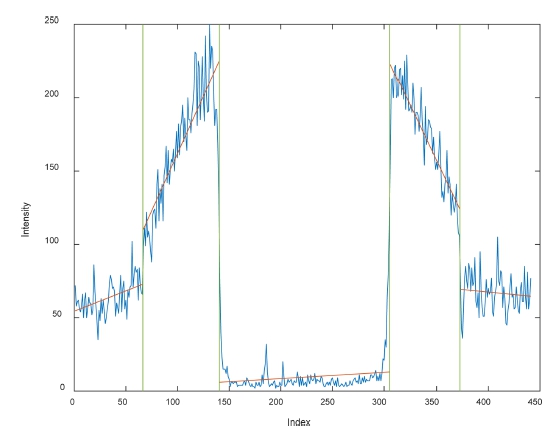
With this method, the experimental results shown in Fig. 3 were segmented into five groups, as shown in Fig. 9.
The intensity changed depending on the type of reflection surface. The results show the water surface in the center, the left and right sides of the center, which were the plates above the reservoir, and both ends of the floor.
2.3 Experiment on Various Ground Conditions
Potholes or puddles in front of the driving direction must be detected using LiDAR when driving on rough outdoor terrain. Thus, three experimental environments, as shown in Fig. 10(a) were studied: a water puddle in which the reservoir was buried, a pothole after the reservoir was removed (Fig. 10(b)), and the pothole filled with soil to flatten it (Fig. 10(c)).
First, for the puddle, the coordinates of the reflection point among the LiDAR output values for one vertical plane are shown as circles in Fig. 11. The water puddle was located 1.37 to 1.73 m ahead, the water depth was 0.08 m, and the height of the LiDAR origin was 0.6 m above the ground. The measurements of the reflected portion of the water surface did not indicate the location or depth of the water, and many measurements repeatedly had values of 0, as shown in Fig. 11. This was a measurement error in which the measured distance was 0, thereby the coordinate value calculated from this was an output of 0.
The results of group segmentation using linear regression for the output intensity and index values are shown in Fig. 12. The environment was divided into three groups: ground, central water, and ground.
Fig. 13 shows the location of the water puddle, with the coordinate values belonging to the central group highlighted in green.
Second, after the reservoir was removed, the intensity of the LiDAR measurements for the pothole formed a single group, as shown in Fig. 14.
Finally, the intensity measured after filling the pothole with soil and flattening it formed a group, as shown in Fig. 15, similar to the case with the pothole. We confirmed that only the cases in which water was present could be segmented into groups based on intensity values.
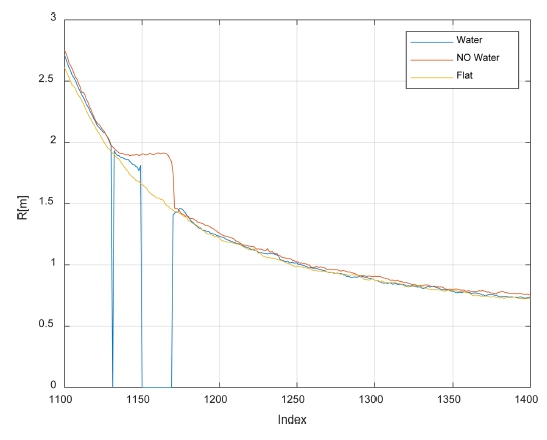
A method of detecting a pothole using distance R was published in [8]. For the three cases above, R with respect to the index is shown in Fig. 16.
Flat ground and potholes can be recognized by detecting changes in [8]. For puddles, some of these values are 0 in the area reflected on the water, but by classifying groups based on intensity, the ground and existence of puddles can be confirmed.
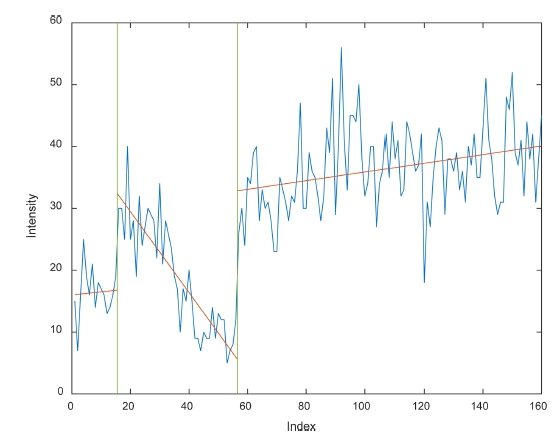
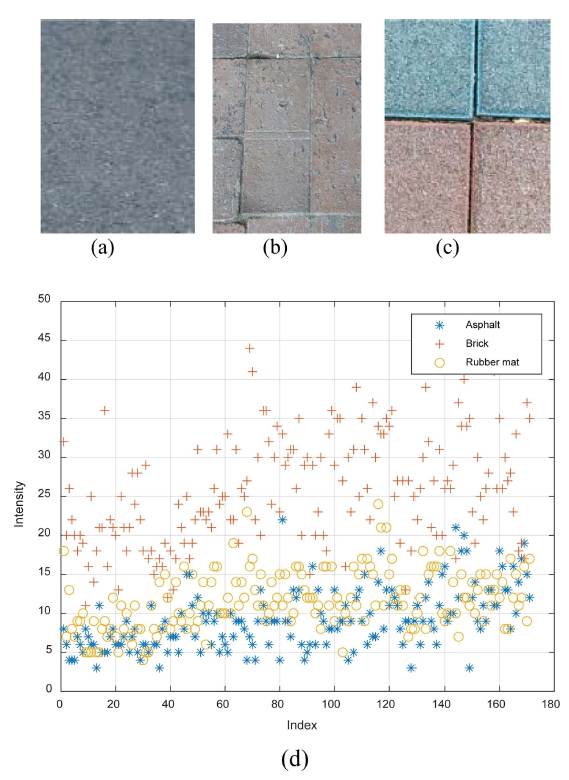
Measurements of intensity were performed on various surfaces including the asphalt, the brick and the rubber mat. Fig. 17 shows the results. We verified that a uniform surface may be modeled as linear function, while the brick surface shows larger variance.
The Lidar has an internal 3-axis accelerometer and the update rate is 100 Hz. By monitoring the vertical acceleration, we can detect any abnormal vertical shock. This may cause incorrect point cloud reading. However, the intensity reading may not be directly affected.
3. Geometry Analysis
The mobile robot used in the experiment was a WeGo-ST from WeGo Robotics, which was equipped with a LiDAR on the upper front part.
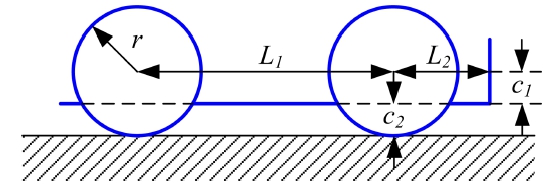
When driving forward and a puddle of water is detected ahead, the possibility of passing through it must be determined, which is essential for planning a real-time path. The main dimensions shown in Fig. 18 are a wheel radius of r = 0.165 m, distance between the wheel axles of L1 = 0.498 m, distance from the front wheel axle to the endpoint of the front end of the car body of L2 = 0.216 m, distance between the wheel axle and the bottom of the car body of c1 = 0.023 m, and height from the bottom of the car body to the ground of c2 = 0.142 m.
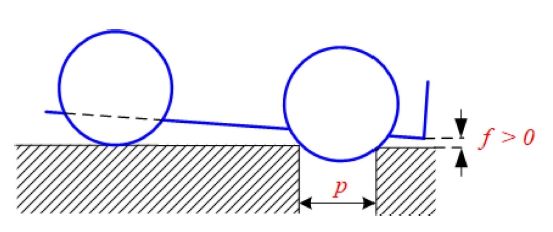
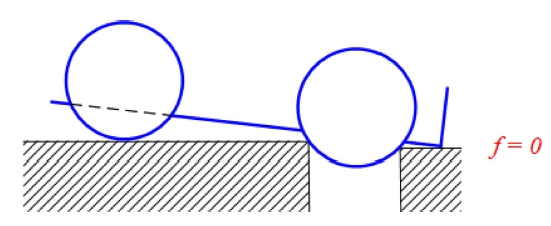
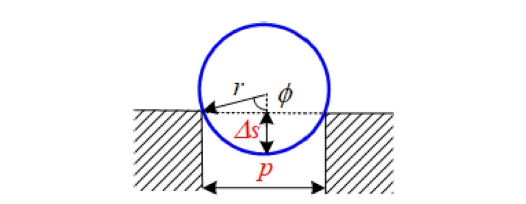
We assumed that the torque output of the drive motor and the friction between the wheels and the ground were sufficiently large and that the height of the ground surface after passing through the puddle was the same as the height before passing through. The height between the lowest part of the front part of the car body and the ground was f, which could pass the pothole only if f>0 , as shown in Fig. 20. As shown in Fig. 21, a geometric relationship was obtained when the bottom of the front end of the car body touched the ground, when f = 0. A wheel whose radius is r spanning a pothole width of p is shown in Fig. 22. The angle φ related to the change in height of the center of the wheel axis ∆s, is derived using Eqs. (13) and (14):
| (13) |
| (14) |
From these two equations, ∆s is expressed in terms of wheel radius r and width p as in Eq. (15).
| (15) |
The tilt angle Ψ of the car body due to the descent of the wheel axis by Δs is
| (16) |
The amount of change in height at the bottom-end point of the front car body is (L1+L2)sinΨ. Therefore, the height f between the lowest part of the front part of the car body and the ground, as shown in Fig. 20, is represented by Eq. (17).
| (17) |
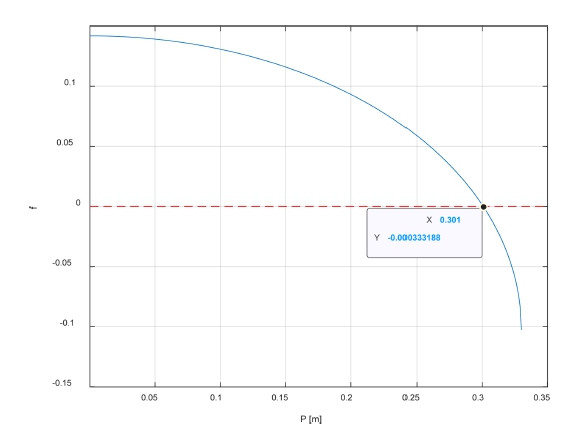
Substituting the car body dimensions used in the experiment, the maximum width that can be crossed safely is when the value of f obtained by setting Eq. (17) is positive, which is a function of the width of the puddle p. Using Eq. (17), the change in value f according to the change p is shown in Fig. 23.
If both wheels are placed on the same level of the ground(p = 0), then f = c2 = 0.142 as predicted in Fig. 19. If the width is less than 0.301m, the vehicle body can cross without colliding with the ground. The above analysis applies equally to puddles and potholes. A study on whether passage is possible when a curb exists was published in [8].
4. CONCLUSIONS
In this paper, we introduce a method of detecting puddles on a driving surface using the intensity of LiDAR measurements. Using the basic characteristics of light intensity, the intensity measurements can be segmented into groups using the linear regression method to distinguish water puddles on the driving surface from those on the ground. Even when a partial error occurs in the measured distance value owing to the characteristics of the water surface, the intensity provides sufficient information to enable group segmentation. If potholes or puddles are present on a planned driving route, determining whether they can be crossed is essential for real-time path planning. An analysis was performed to determine the maximum width that could be crossed for the given dimensions of a robot's body and wheels. In addition to the intensity, the reflectivity, another LiDAR measurements, will be useful for identifying the surface.
Acknowledgments
This research was supported by the Basic Research Project of Korea Institute of Machinery and Materials (Project ID: NK242I).
REFERENCES
-
P. Sun, X. Zhao, Z. Xu, R. Wang, and H. Min, “A 3D LiDAR Data-Based Dedicated Road Boundary Detection Algorithm for Autonomous Vehicles”, IEEE Access, Vol. 7, pp. 29623-29638, 2019.
[https://doi.org/10.1109/ACCESS.2019.2902170]

-
K. Wang, N. Jiasheng, and L. Yanqiang, “A Robust LiDAR State Estimation and Map Building Approach for Urban Road”, Proc. of 2021 IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), pp. 502-506, Nanchang, China, 2021.
[https://doi.org/10.1109/ICBAIE52039.2021.9390023]

-
L. Gong, Y. Zhang, Z. Li, and Q. Bao, “Automated Road Extraction from LiDAR Data Based on Intensity and Aerial Photo”, Proc. of 2010 3rd Int. Congress on Image and Signal Processing, pp. 2130-2133, Yantai, China, 2010.
[https://doi.org/10.1109/CISP.2010.5647354]

-
M. Okhrimenko and C. Hopkinson, “A Simplified End-User Approach to Lidar Very Shallow Water Bathymetric Correction”, IEEE Geosci. Remote Sens. Lett., Vol. 17, No. 1, pp. 3-7, January, 2020.
[https://doi.org/10.1109/LGRS.2019.2915267]

-
K. Higashimoto, H. Fukushima, K. Kamitani, and N. Chujo, “Identification of Road Surface Condition on Undeveloped Roads: Aiming for Remote Car Driving”, Proc. of 2021 IEEE 10th Global Conference on Consumer Electronics (GCCE), pp. 777-781, Kyoto, Japan, 2021.
[https://doi.org/10.1109/GCCE53005.2021.9621967]

-
J. Kim, K. Kwak, and K. Bae, “Experimental Analysis and Internal Calibration of the 3D LIDAR Reflectivity”, J. Inst. Control Robot Syst., Vol. 23, No. 7, pp. 574-582, 2017.
[https://doi.org/10.5302/J.ICROS.2017.17.0086]

-
J. Kim, S. Ahn, J. Min, and K. Bae, “Analysis of Traversable Candidate Region for Unmanned Ground Vehicle Using 3D LIDAR Reflectivity”, Transact. Korean Soc. Mech. Eng. A, Vol. 41, No. 11, pp. 1047-1053, 2017.
[https://doi.org/10.3795/KSME-A.2017.41.11.1047]

-
M. Lee, M. H. Cha, H. Lee, and S. Lee, “Lidar Measurement Analysis for Detection of Down-Curbs and Up-Curbs”, J. Inst. Control Robot. Syst., Vol. 29, No. 2, pp. 126-134, 2023.
[https://doi.org/10.5302/J.ICROS.2023.22.0197]