패턴사전과 비정형성을 통한 이상치 탐지방법 적용

1. 서 론

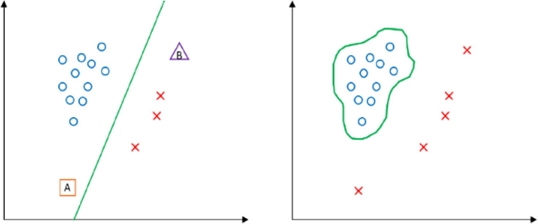
이상치(Anomaly)를 정의하기는 어렵지만, 특히 공학 및 과학 분야를 비롯한 다양한 분야에서 이상치가 존재하는 것은 분명하다. 센서 및 의료 분야에서도 이상치를 탐지하는 것은 중요하며, 다양한 이상치 탐지(Anomaly Detection) 방법이 개발되고 적용되고 있다. 일반적으로 이상치는 정상 분포와 크게 벗어난 패턴으로 정의되며, 이상치 탐지는 이러한 패턴을 탐지하는 것이라 할 수 있다[1]. 하지만 이상치 탐지는 지도학습(Supervised learning)을 바탕으로 한 정상 패턴과 비정상 패턴을 분류하는 이진분류와는 차이가 있으며, Fig. 1에서와 같이 새로운 관측값(이상치) A와 B가 제시되었을 때, 이진분류에서는 A를 이상치로 분류할 수 없지만, 이상치 탐지 문제에서는 A와 B모두를 이상치로 판단할 수 있다[1-3]. 또한, 이상치 탐지 문제를 해결할 때는 대부분 이상 샘플에 대한 정답값(라벨)이 없기 때문에 비지도 학습(Unsupervised learning) 또는 준지도 학습(Semi-supervised learning) 문제로 분류된다[4,5]. 종종 주어진 데이터 셋에서 이상치를 쉽게 구별할 수 있는 경우도 있기 때문에 이상치 탐지가 어려운 문제라고 생각하지 않을 수 있다.

Fig. 1.

Binary classification vs. Anomaly detection

그러나 실제로 이상치 탐지문제는 쉽게 해결하기 어렵고, 이를 어렵게 만드는 몇 가지 원인이 있다. 첫 번째, 각 도메인에서의 이상치에 대한 정의는 다를 수 있으므로, 특정 도메인에 대해 개발된 방법을 다른 도메인에 적용하는 것이 어렵다. 두 번째, 잠재적인 이상 데이터의 크기와 발생 빈도는 쉽게 파악할 수 없다. 세 번째, 이상치에 대한 샘플획득과 라벨링에 어려움이 있으며, 극도의 데이터 불균형이 있을 수 있다[1].

이러한 문제를 해결하기 위해 최근 연구에서는 패턴 사전(Pattern dictionary)과 비정형성(Atypicality)을 기반으로 시퀀스 데이터에서 이상치를 탐지하는 문제를 다루었고[6], 이를 위한 보편적이고 비모수적 이상치 탐지 방법을 제시하였다. 해당 방법론 에서는 훈련 및 테스트 데이터가 주어지면 패턴 사전을 통하여 훈련 데이터의 모든 패턴을 파악한다. 또한, 패턴사전은 테스트 데이터 시퀀스를 순차적으로 분석 및 압축하는데 사용된다. 그 후, 분석된 구문의 수 또는 압축된 테스트 데이터의 코드 길이를 이상 점수로 활용한다. 즉, 테스트 데이터의 분석된 구문 수가 적거나 압축된 코드 길이가 짧을수록 훈련 및 테스트 데이터 패턴 간의 유사성이 더 높다고 판단하며, 상대적으로 코드 길이가 긴 테스트 데이터는 이상치로 간주한다. 또한, 시퀀스의 비정형성을 측정하여 패턴사전 방법과 함께 사용함으로써, 이상치 탐지의 정확성을 향상시킨다.

육군에서 추진하는 Army Tiger 4.0의 핵심인 워리어 플랫폼(개인전투체계)에서도 많은 장비들과 센서들이 사용된다. 특히, 워리어 플랫폼에서는 개인의 생존성과 전투력을 극대화하기 위해서 전투원의 신체 상태를 파악하는 웨어러블 센서가 사용되며, 각종 센서들이 드론 및 유ㆍ무인 복합 무기체계에 장착되어 사용되므로 전ㆍ평시 전장환경에서 장비 및 시스템의 이상유무를 판단하는 것은 작전지속성 측면에서 매우 중요하다.

따라서, 본 논문에서는 패턴사전 방법이 센서에서 발생할 수 있는 다양한 이상치를 탐지할 수 있는지 보인다. 또한, 패턴사전 방법이 적은 훈련데이터 만으로도 이상치 탐지에 활용이 가능한 것을 실제 심전도 데이터를 통해 보임으로써, 향후 워리어 플랫폼 등 미래무기체계 시스템에 적용이 가능함을 시사한다.

2. 연구 방법

2.2 패턴사전을 통한 이상치 탐지 프레임워크

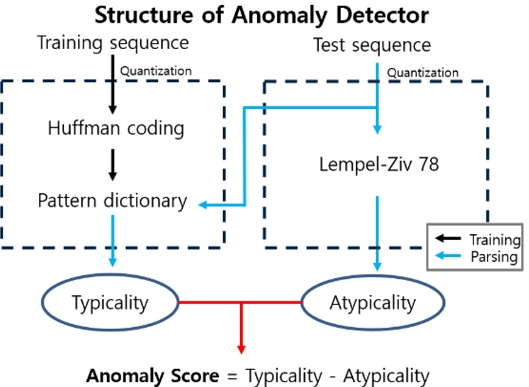
본 논문에서 사용한 이상치 탐지 방법은 Fig. 2에서 보는 바와 같이, 먼저 훈련 시퀀스(또는 시계열 데이터)를 양자화한다. 양자화된 훈련 시퀀스를 허프만 코딩(Huffman coding)을 통하여 패턴 사전을 생성한다. 이 과정 까지가 이상치 탐지 방법의 훈련과정이다. 이후 테스트 시퀀스는 두가지 방법으로 분석이 된다. 첫 번째, 훈련과정에서 생성된 패턴사전을 통해서 정형성 (Typicality)을 측정한다. 그 후 패턴사전과는 별개로 범용소스코드(Universal source coder)중 하나인 렘펠-지브78(Lempel-Ziv78, LZ78)[8] 알고리즘을 통해서 테스트 시퀀스의 비정형성 (Atypicality)을 측정한다. Fig. 2에서 보는 것 과 같이, 이 과정을 통해서 테스트 시퀀스에 대한 두 가지 특성을 얻게 되고 정형성과 비정형성의 차이 값을 이상치 점수로 부여하여 테스트 시퀀스가 이상 시퀀스 인지 아닌지 판단한다.

Fig. 2.

Structure of a proposed anomaly detection method

2.3 패턴사전의 생성

유한개의 알파벳 집합에서 추출된 길이가 L인 하나의 시퀀스(훈련 데이터) {x_n, n = 1, ..., L}를 고려해 보자. 이상치 탐지를 위해 필요한 가장 첫번째 단계는, 시퀀스 내에 있는 패턴 중 길이가 D_max 보다 작은 모든 패턴들을 통해 패턴사전을 생성하는 것이다. 우리는 생성된 패턴사전을 D라 하며 $$ S_{\mathrm{D}}\left(x_1^L\right)$$을 관측된 모든 패턴의 집합이라 한다.

예시 1. 훈련 데이터 x = ABACADABBACCADDABABACADA가 유한 알파벳 집합 X = {A,B,C,D}에서 D_max = 2의 조건으로 생성된 패턴 집합은 S_D(x) = {A,B,C,D,AB,BA,AC,CA,AD,DA,BB,CC,DD} 이다.

패턴 사전이 훈련 기반 고정 소스 코더(데이터 의존적 소스 코더로 [6]에서 정의됨)로 사용되기 때문에, 코드 길이를 최소화하는 효율적인 구조에 관심이 있다. 가장 간단한 방법은 길이가 d인 (1≤d≤D_max) 패턴만을 고려하고 단일 인덱싱 접근 방식을 사용하는 것이다. 이 접근 방식을 단일 레벨 사전(Unit-level dictionary) 방법이라 한다. 또 다른 방법은 훈련 시퀀스의 모든 패턴을 길이별로 분리하여 사용하는 것이다. 길이 별 패턴의 집합을 S_D⁽¹⁾, S_D⁽²⁾, …, S_D^{(D max)} 로 나타내며, 이를 $$ {\mathit{S}}_{\mathrm{D}}={\mathrm{U}}_{d=1}^{{\mathrm{D}}_{max}}{\mathit{S}}_{\mathrm{D}}^{\left(d\right)}$$로 정의하고 다중 레벨 사전(Multi-level dictionary)이라 한다. 본 논문에서는 이전 연구[6]에서 도출된 결과에 따라, 일반적으로 시퀀스에 더 짧은 코드길이를 부여하는 다중 레벨 사전방법을 사용한다.

예시 1에서 제시된 훈련 시퀀스를 바탕으로 패턴 사전을 생성한 결과는 Table 1과 같으며, $$ \mathrm{P}\mathrm{r}\left(x_1^d\right)$$는 각 패턴들의 빈도에 따른 확률을 나타내고, $$ L_{\mathrm{D}}\left(x_1^L\right)$$는 이에 따라 허프만코딩을 통해 각 패턴에 부여한 코드길이다.

Table 1.

Multi-level dictionary with x = ABACADABBACCADDABABACADA, X = {A,B,C,D}, Dmax = 3.

2.4 테스트 시퀀스 분석

2.4.1. 정형성(Typicality)

주어진 테스트 시퀀스 $$ x_1^l=\left\{x_n,n=1,\dots ,l\right\}$$를 훈련 시퀀스를 통해 생성된 패턴사전 D (D_max<1)를 통해 분석하고자 한다. 테스트 시퀀스 $$ x_1^l$$은 c개의 구문 $$ x_{v_1}^{v_2-1}$$, $$ x_{v_2}^{v_3-1}$$, …, $$ x_{v_c}^l$$로 분석되며 이때, v_i는 i번째 구문의 시작 인덱스를 의미하며, $$ x_{v_i}^{v_{i+1}-1}$$는 패턴사전 D에 포함된 패턴 중 하나이다. 따라서, 분석된 시퀀스의 집합을 $$ {\mathit{S}}_{\mathrm{D}}\left(x_1^l\right)=\left\{x_{v_1}^{v_2-1},x_{v_2}^{v_3-1},\dots ,x_{v_c}^l\right\}$$로 정의할 수 있다. v₁은 1부터 시작하며 v₂≤l과 v₂≤D_max를 모두 만족하는 가장 큰 v₂를 찾으며 이때 v₂는 $$ x_{v_1}^{v_2-1}\in \mathrm{D}$$지만, $$ x_{v_1}^{v_2}\notin \mathrm{D}$$이다. 이러한 방법론은 최초 독립적인 시퀀스들에 대한 상대적 엔트로피를 측정하기 위해서 도입되었다[8]. 아래 Algorithm 1 에서는 패턴 사전 분석(Pattern Dictionary Parser)의 진행과정을 나타내고 있으며, 최종 코드 길이는 수식(1)과 같이 표현한다. 수식(1)에서 얻은 코드길이의 값, 즉 정형성은 이상치 점수로 사용될 수 있는데, 이를 통해 이상치를 탐지하는 방법을 PDD(Pattern Dictionary for Detection)라 정의한다.

$\[ L_T\left(x_1^l\right)={\mathrm{\Sigma }}_{i=1}^c{L}_D\left(x_{v_i}^{v_{i+1}-1}\right)+c {\mathrm{l}\mathrm{o}\mathrm{g}}_2{D}_{max}\dots \]$

(1)

, where $$ \mathrm{c}=\left|S_D\left(x_1^l\right)\right|$$, the number of parsed sequences.

Algorithm. 1.

Pattern Dictionary Parser

2.4.2. 비정형성(Atypicality)

특정 시퀀스가 자주발생 되는 패턴에 기반한 최적의 코드를 사용하는 것 보다 그 자체로 더 적은 비트로 설명(코딩)될 수 있다면 그 시퀀스는 비정형성을 가진다[9]. 2.4.1에서 설명된 정형성을 이상치 점수로 그대로 사용할 수 있지만, 정형성 만으로 이상치 탐지를 수행했을 경우, 이상치를 탐지하지 못하는 경우가 발생하기 때문에 비정형성을 사용한다. 직관적인 예로, 확률 변수 X가 0과 1로 구성되는 이진 시퀀스를 고려해보자. 길이가 L이고 P(X = 1) = p인 이진 시퀀스(L개의 비트 중 각 비트가 1일 확률은 p이고, 0일 확률은 1-p이다.)에 우리가 탐지해야 하는 이상 이진 시퀀스 $$ \mathrm{P}\left(\mathrm{X}=1\right)=\widehat{p}$$ 가 포함되어 있다고 가정한다. 이때 $$ p=\frac{1}{2}$$(정상 시퀀스에서는 각 비트가 1일 확률이 $$ \frac{1}{2}$$)이고, $$ \widehat{p}$$ = 1 (이상 시퀀스에서 각 비트가 1일 확률은 1)이면, 비정형 인코더는 이상 시퀀스를 탐지할 수 있지만, 정형 인코더(패턴사전)는 탐지하지 못한다. 다른 경우로, $$ p=\frac{1}{3}$$ 이고 $$ \widehat{p}=\frac{2}{3}$$ 이면, 정형 인코더는 이상 시퀀스를 탐지할 수 있지만, 두 시퀀스의 엔트로피는 동일하기 때문에 비정형 인코더는 이상 시퀀스를 탐지할 수 없다. 즉, 패턴사전방법이 이상치를 더욱 잘 탐지할 수 있도록 비정형성과 함께 사용된다. 본 논문에서 사용하는LZ-78 알고리즘을 통해 얻은 시퀀스 x에 대한 코드길이는 수식(2) 같이 나타내며, 이전 연구 [6,9]에서 증명된 바와 같이 이상치 점수는 $$ L_T\left(x_1^l\right)-L_A\left(x_1^l\right)$$ 값을 사용한다. 또한, 해당 값을 통하여 이상치를 탐지하는 방법을 PDA(Pattern Dictionary Based Atypicality)라 정의한다.

$\[ L_A\left(x_1^l\right)=\left|S_{LZ}\left(x_1^l\right)\right|\left[{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left|D_{max}\right|+1\right]\dots \]$

(2)

3. 실 험

3.1 Mackey-Glass Time Series 실험

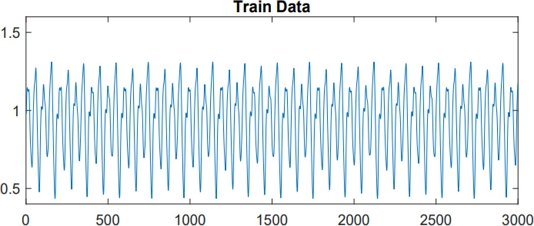
이 장에서는 중간에 이상 시퀀스가 삽입된 Mackey-Glass (MG) 시퀀스 데이터에 대하여 제안된 이상치 탐지 방법(PDA, PDD)의 적용 결과를 나타낸다. MG 시퀀스는 비선형 시간 지연 미분 방정식에서 생성되며, 이는 복잡한 동적 현상이 생리학적 제어 시스템에 발생하는 것을 나타내기 위해 처음 도입되었다[12]. 비선형 미분 방정식은 $$ \frac{dx\left(t\right)}{dt}=-ax\left(t\right)+\frac{bx\left(t-\delta \right)}{a+x^{10}\left(t-\delta \right)}$$, t≥0형태를 가지며, 여기서 a, b 및 δ는 상수이다. 훈련 데이터는 Fig. 3과 같이 a = 0.2, b = 0.1, δ = 17로 설정된 길이가 3000(1≤t≤3000)인 MG시퀀스로 생성되었다. 테스트 데이터의 경우 센서에서 탐지될 수 있는 4가지 이상 경우를 가정하고 길이가500인 시퀀스 생성하였다. 생성된 이상 시퀀스는 훈련 데이터와 동일한 파라미터로 생성된 길이가 1000인 MG시퀀스 샘플 내부에 포함시켜 총 길이가 1500인 테스트 시퀀스를 만들었다.

Fig. 3.

Training sequence generated by Mackey-Glass equation with a = 0.2, b = 0.1, δ = 17.

Fig. 3과 4는 훈련 데이터(시퀀스)와 테스트 데이터(시퀀스)를 나타내며, 본 실험에서는 PDA와 PDD가 센서 데이터에 적용 가능함을 보이기 위해 Fig. 4와 같이 4가지 이상 경우를 제시한다. 모델에 대한 성능 측도는 ROC-AUC(Receiver Operating Characteristic - Area Under Curve)와 PR-AUC(Precision-Recall - Area Under Curve)를 사용하였다.

Fig. 4.

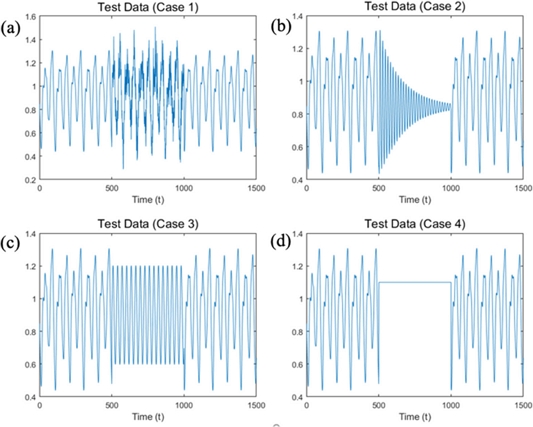
Anomalies are embedded from 501 to 1000; (a) Noise: MG with a = 0.2, b = 0.1, δ = 17 and gaussian noise with std = 0.1. (b) Converging: MG with a = 0.7, b = 0.7, δ = 17. (c) Different type of sequence: Sine wave (frequency = 0.03). (d) Flat signal: f(t) = 1.1 .

3.1.1. 실험 데이터

2장에서 제시된 패턴사전을 통한 이상치 탐지방법이 다양한 센서에서 적용이 가능한지 확인하기 위해 발생가능 한 4가지 경우를 가정하였다. 첫번째, 정상 신호에 노이즈가 발생한 경우, 두번째, 다른 패턴의 신호가 발생할 경우, 세번째, 신호가 소실될 경우, 네번째, 같은 값의 신호가 지속적으로 발생할 경우이다. 본 실험에서는 테스트 시퀀스 $$ x_1^l$$에서 분석되는 부분 시퀀스의 길이는 100으로 설정하였고($$ x_t^{t+99},t=1,\dots ,1500$$), D_max = 40, |X| = 45 으로 설정되었다.

3.1.2. 실험 결과

Table 2의 결과와 같이 Mackey-Glass로부터 생성된 시퀀스 사이에 나타난 4가지 다른 이상 시퀀스에 대하여 PDA와 PDD는 높은 ROC-AUC와 PR-AUC수치를 가짐으로써, 다양 한 경우의 이상치 탐지에 적용될 수 있음을 보였다. 또한, 모든 경우에서 시퀀스의 비정형성을 고려한 PDA가 PDD보다 나은 성능을 보였다

Table 2.

Comparison of the results from PDA and PDD with different cases.

3.2 PTB Diagnostic ECG Database 실험

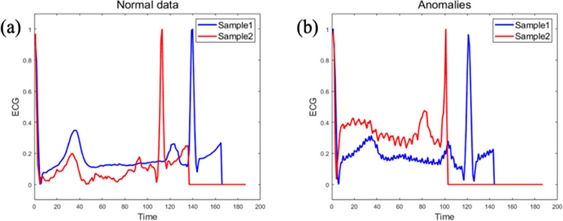
PTB Diagnostic ECG 데이터 셋은 290명의 심전도(ECG) 기록으로 구성되어 있다[10]. 데이터는 심근경색(Myocardial Infarction, MI)으로 진단된 심전도와, 정상 심전도 데이터로 구분되어 있으며, 심전도 데이터는 12개의 리드로부터 1000 Hz의 주파수로 획득되었고, 리드 I I로 얻어진 데이터를 125Hz로 축소하여 이상치 탐지 방법을 적용하였다[11]. Fig. 5는 해당 데이터의 샘플을 나타내며, 데이터의 특성상 길이가 다른 시퀀스가 발생하는데 최대 길이보다 짧은 시퀀스들은 제로패딩으로 처리하였다.

Fig. 5.

Samples of (a) normal and (b) anomaly case from PTB Diagnostic ECG Database.

PDA와 PDD가 실제 센서 또는 의료분야에서 활용될 수 있는지 확인하기 위하여 해당 데이터에 적용하였다. 3.2.1과 같이 실험데이터를 구성하였으며, 특히, 워리어 플랫폼의 특성에 따라 개인별 신체특성 및 장비에 활용 가능성을 확인하기 위하여 훈련 데이터의 크기에 따라 실험을 구성하였다. 또한, 이상치 탐지에서도 높은 성능을 보이는 오토인코더(AutoEncoder, AE)와도 성능을 비교하였다. 본 실험에서 사용된 오토인코더의 인코더는 Fig. 3에 제시된 바와 같이, 3개의 Conv1D layer로 구성되며 필터의 개수는 64-32-16개이다. 커널의 크기는 3이며, 각 레이어 마다 배치정규화와 맥스풀링을 적용하였고, 활성화 함수는 렐루함수를 사용하였다. 디코더 부분에서는 맥스풀링대신 업샘플링을 통해서 대칭을 구조를 이루었다. 모델의 학습간 배치사이즈는 64, epoch는 100회, 손실함수는 평균절대오차(MAE), 최적화 알고리즘은 Adam을 사용하였다. 또한, 과적합을 방지하기 위해 EarlyStopping을 사용하고, 최적의 가중치를 저장하여 테스트에 사용하였다. 이러한 컨볼루션 기반의 오토인코더는 정상 훈련 데이터만을 통해서 학습하고 학습된 결과를 바탕으로 테스트 데이터에 이상치 점수를 부여하는 점에 있어 논문에서 제시하는 패턴사전방법과 공통점이 있다. 하지만, Fig. 2에서 PDA의 분석(Parsing)부분은, 오토인코더에서 디코더(Decoder)부분과 유사하지만, PDA에서 비정형 (Atypicality)를 구하는 과정은 훈련데이터에 영향을 받지 않는다는 점에서 오토인코더와 차이점이 있다.

3.2.1. 실험 데이터

훈련데이터의 경우 이상치 탐지의 가장 큰 어려움 중 하나인 이상 데이터의 획득에 대한 어려움을 가정하여 정상데이터만으로 구성하였다. 또한, 이상치 탐지 문제해결에서는 정상데이터의 비율이 이상데이터의 비율보다 높다. 따라서, 모델의 성능을 검증하기 위해 사용된 테스트 데이터는 실험 3.1의 조건과 동일하게 정상데이터를 1000개, 이상데이터를 500개씩 중복되지 않도록 임의 추출하여 구성되었다.

3.2.2. 실험 결과

실험은 같은 조건에서 임의의 훈련 데이터와 테스트 데이터를 추출하여 100회 반복 시행되었다. Table 3의 결과와 같이 PDA와 PDD는 적은 훈련데이터만으로 오토인코더(AE)보다 높은 ROC-AUC의 수치를 얻었다. 인공신경망 모델의 특성에 따라 훈련데이터가 3000개 이상으로 충분할 경우, 오토인코더(AE)의 성능이 PDA와 PDD보다 근소하게 높았다.

Table 3.

Comparison of the results from PDA, PDD, and AE with different sizes of training samples. The parameters of PDA and PDD: Dmax = 40 |X| = 45. (μ ± σ representation is used where μ is the mean and σ is the standard deviation)

실험결과에 따라 PDA와 PDD는 적은 양의 훈련 데이터(≤2000)를 통해서 오토인코더 보다 정상데이터의 패턴을 빠르게 학습하는 것을 알 수 있었고 이를 통해 실제 데이터에도 적용이 가능함을 알 수 있었다.

4. 결 론

본 연구에서는 패턴사전과 비정형성을 통한 시퀀스 데이터의 이상치 탐지방법의 활용에 대해서 보고했다. 일반적으로 이상치 탐지 문제에서는, 이상데이터의 수집과 라벨링이 어렵기 때문에, 정상데이터만으로 학습을 하고 이상치를 분류해야 하는 경우가 많다. 3.1에서는 Mackey-Glass 방정식을 통해 생성된 시계열 데이터를 통해서 PDD 및 PDA가 센서에서 발생할 수 있는 다양한 이상치에 대하여 적용이 가능함을 보였다. 또한 3.2에서는 PDD와 PDA를 실제 심전도 데이터에 적용함으로써, PDD와 PDA가 적은 훈련데이터를 통해 정상 패턴을 학습하고, 이를 바탕으로 이상치 탐지가 가능하다는 것을 보였다. 이를 통해 향후 PDD와 PDA가 육군의 개인 전투체계인 워리어 플랫폼에도 적용이 가능할 것으로 사료된다.

Acknowledgments

본 연구는 2023년 미래전략기술연구소 AI연구개발센터의 지원을 받아 수행되었습니다(23-AI-07).

REFERENCES

• V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection: A survey”, ACM Comput. Surv., Vol. 41, No. 3, pp. 1-58, 2009. [https://doi.org/10.1145/1541880.1541882]
• I. Steinwart, D. Hush, and C. Scovel, “A Classification Framework for Anomaly Detection”, J. Mach. Learn. Res., Vol. 6, pp. 221-232, 2005.
• N. Elmrabit, F. Zhou, F. Li, and H. Zhou, “Evaluation of machine learning algorithms for anomaly detection”, prof. of 2020 international conference on cyber security and protection of digital services (cyber security), pp. 1-8, Dublin, Ireland, 2020. [https://doi.org/10.1109/CyberSecurity49315.2020.9138871]
• M. E. Celebi and K. Aydin, Eds., Unsupervised learning algorithms, Springer Cham, Switzerland, p. 103, 2016. [https://doi.org/10.1007/978-3-319-24211-8]
• V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection for discrete sequences: A survey”, IEEE Trans Knowl. Data Eng., Vol. 24, No. 5, pp. 823-839, 2010. [https://doi.org/10.1109/TKDE.2010.235]
• E. Sabeti, S. Oh, P. X. K. Song, and A. O. Hero, “A pattern dictionary method for anomaly detection”, Entropy, Vol. 24, No. 8, pp. 1095(1)-1095(26), 2022. [https://doi.org/10.3390/e24081095]
• V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection for discrete sequences: A survey”, IEEE Trans. Knowl. Data Eng., Vol. 24, No. 5, pp. 823-839, 2010. [https://doi.org/10.1109/TKDE.2010.235]
• J. Ziv and A. Lempel, “Compression of individual sequences via variable-rate coding”, IEEE Trans. Inf. Theory, Vol. 24, No. 5, pp. 530-536, 1978. [https://doi.org/10.1109/TIT.1978.1055934]
• A. Høst-Madsen, E. Sabeti, and C. Walton, “Data discovery and anomaly detection using atypicality: Theory”, IEEE Trans. Inf. Theory, Vol. 65, No. 9, pp. 5302-5322, 2019. [https://doi.org/10.1109/TIT.2019.2917669]
• R. Bousseljot, D. Kreiseler, and A. Schnabel, “Nutzung der EKG-Signaldatenbank CARDIODAT der PTB über das Internet”, Biomed. Tech., Vol. 40, pp. 317-318, 1995. [https://doi.org/10.1515/bmte.1995.40.s1.317]
• M. Kachuee, S. Fazeli, and M. Sarrafzadeh, “Ecg heartbeat classification: A deep transferable representation”, proc. of 2018 IEEE Int. Conf. Healthc. Inform., pp. 443-444, New York, USA, 2018. [https://doi.org/10.1109/ICHI.2018.00092]
• M. C. Mackey and L. Glass, “Oscillation and chaos in physiological control systems”, Science, Vol. 197, No. 4300, pp. 287-289, 1977. [https://doi.org/10.1126/science.267326]